给定一个 n个点 m条边的有向图，点的编号是 1到 n，图中可能存在重边和自环。

请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1。

若一个由图中所有点构成的序列 A满足：对于图中的每条边 (x,y)，x在 A中都出现在 y之前，则称 A是该图的一个拓扑序列。

输入格式

第一行包含两个整数 n和 m。
接下来 m行，每行包含两个整数 x和 y，表示存在一条从点 x到点 y 的有向边 (x,y)。

输出格式

共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。
否则输出 −1。

数据范围

1≤n,m≤105

输入样例：

3 3
1 2
2 3
1 3

输出样例：

1 2 3

这道题我们的思路就是将我们图中所有的点都计算一下入度是多少，也就是有多少条边是指向当前的点的。
然后我们将所有入度为0的点放入我们的队列中。
然后遍历我们的队列，也就是依次从队列中取出一个元素，将其删掉，然后将这个点指向的边也全部都删掉，然后看看删掉之后，有没有新的点的入度为0，如果有的话，就加入我们的队列。
用一个vector记录我们每次删掉的元素
如果我们的vector的大小跟我们的点总数是相等的，那么我们就是可以得到一个拓扑序列的，只要将我们的vector中的内容全部打印出来就可以了。
如果vector的元素个数跟我们点的总数不相等的话，就返回-1.。

比方说下面这张拓扑图

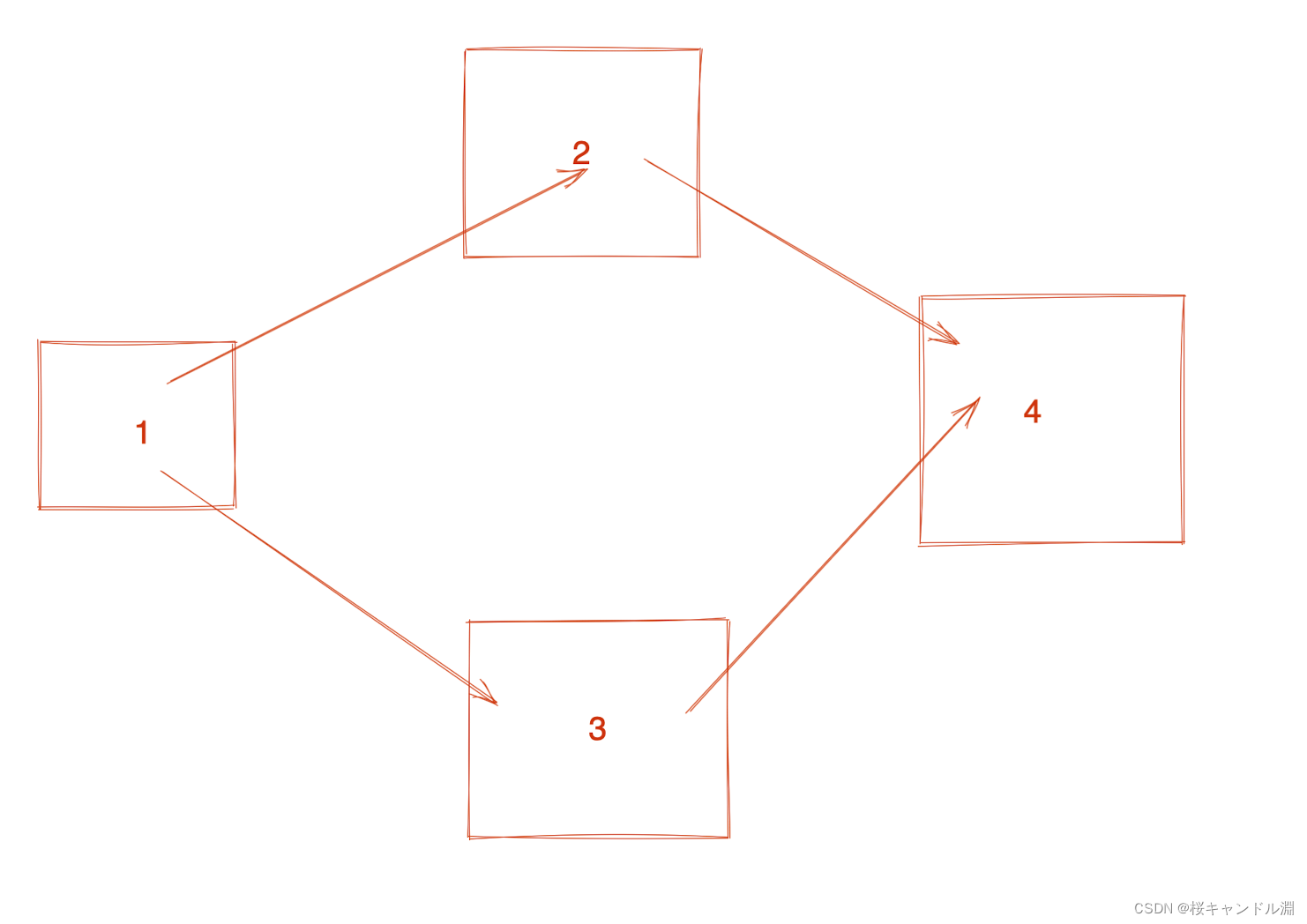
我们1的入度为0，我们就将1加入队列
（我们的队列每次都是取出一个队头的元素，这里就是取出1，也就是pop掉）
将1放入我们的vector中
1->
然后我们将1删掉
删掉之后，我们发现2和3的入度此时也变成了0

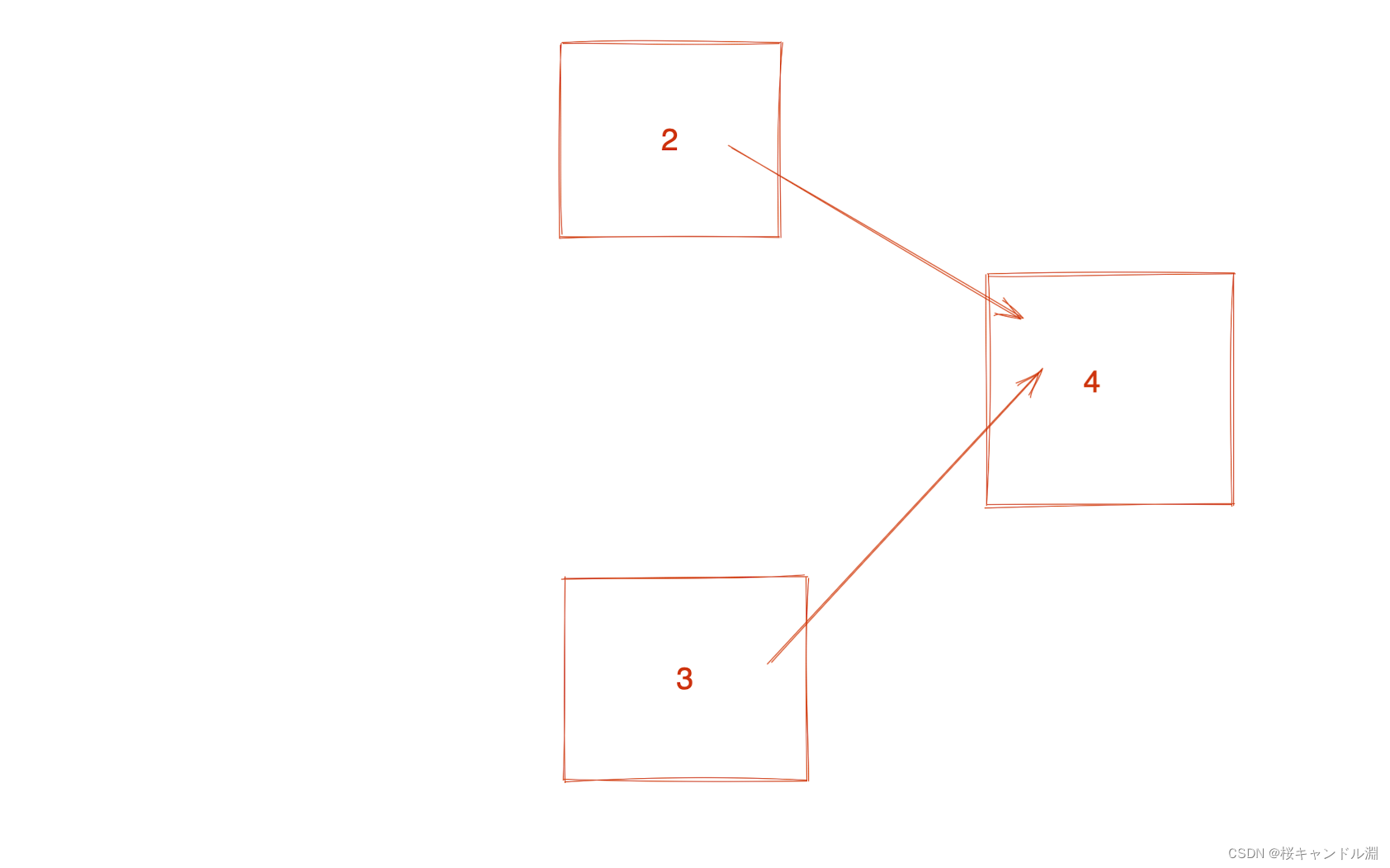
我们将2,3也加入我们的队列，然后将我们的2,3删掉
将2,3放入vector中
1->2->3

最后我们发现4的入度也为0，我们将4加入队列
将4放入vector中
1->2->3->4
然后我们发现没有点可以加入队列了，并且我们的队列在4被pop了之后也空了，此时我们发现vector的大小跟我们数据的个数是相等的，所以我们能够打印出我们的队列

#include<iostream>
#include<vector>
#include<list>
#include<map>
#include<queue>

using namespace std;
const int N=100010;
int number;
map<int,int> m1;
vector<list<int>> record(N,list<int>{});

void add(int a,int b)
{
    record[a].push_front(b);
}

void topo()
{
    int start_point;
    
    queue<int> q1;
    vector<int> v1;

    for(auto&i:m1)
        if(i.second==0) q1.push(i.first);
    while(!q1.empty())
    {
        int head=q1.front();
        q1.pop();
        v1.push_back(head);
        for(auto&i:record[head])
        {
            m1[i]--;
            if(m1[i]==0)
            {
                q1.push(i);
            }
        }
        record[head]={};
    }
    if(v1.size()==number)
    {
        for(auto&i:v1)
        {
            cout<<i<<" ";
        }
        cout<<endl;
    }else{
        cout<<-1<<endl;
    }
}
int main()
{
    int m;
    cin>>number>>m;
    while(m--)
    {
        int x,y;
        cin>>x>>y;
        add(x,y);
        m1[y]++;
        m1[x]+=0;
    }
    topo();
    return 0;
}