1. 前言

在上一篇博客中：Tic-Tac-Toe可能棋局搜索的实现（python）_笨牛慢耕的博客-CSDN博客Tic-Tac-Toe中文常译作井字棋，即在3 x 3的棋盘上，双方轮流落子，先将3枚棋子连成一线的一方获得胜利。Tic-Tac-Toe变化简单，可能的局面和棋局数都很有限（相比中国象棋、日本象棋、围棋等来说连九牛一毛都不到！具体有多少可能的局面以及可能的棋局数，本系列完成以后就可以给出答案了），因此常成为和搜寻的教学例子，同时也是的一道好题目。本系列考虑实现一个Tic-Tac-Toe AI，以由浅入深循序渐进的方式来逐步完成这个实现。https://blog.csdn.net/chenxy_bwave/article/details/128506352 实现了搜索Tic-Tac-Toe游戏的某个棋局的python程序。

接下来的问题是，在Tic-Tac-Toe游戏中总共有多少种可能的棋局呢？注意，棋局是指在两个player交替下棋直到终局的过程中所导致的棋盘状态变化的序列。所以，即便所包含的棋盘状态集合完全相同，但是如果棋盘状态出现的顺序不同的话，也是不同的棋局。

游戏规则、基本表示方法等参考上一篇博客，本文不做赘述。

本文在上一篇的基础上进一步实现搜索Tic-Tac-Toe游戏的所有可能棋局的实现。

2. 算法流程

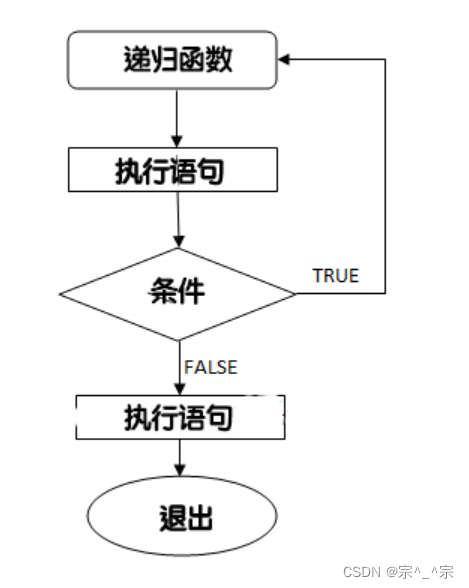
如果只需要搜索某一个可能的棋局，采用深度优先搜索或者广度优先搜索都可以。但是，如果要遍历所有可能的棋局，则需要采用深度优先搜索的方式来实现遍历，也称深度优先路径遍历。

Dfs(path):

       s = path[-1] # 取路径列表中最后一个状态作为当前状态

       查找s的所有邻接节点（即从s状态再下一手棋可能到达的状态）à neighbor_list

       For neighbor in neighbor_list: # 遍历s所有邻接节点

              If neighbor not in path:     # 如果该节点已经在path中则跳过

                     Append neighbor to the end of path

                     If neighbor 是终局状态:

                            将path加入到path_list中去 # path_list是一个全局变量

                     Else:

                            递归调用：dfs(path)

                     Path.pop() # 这个不能少！

主程序中以初始状态开始调用dfs()即可求出所有的路径（Tic-Tac-Toe的所有可能棋局）。

这个算法流程中其实是留了一个坑。。。

3. 代码实现

# -*- coding: utf-8 -*-
"""
Created on Sun Jan  1 16:15:19 2023

@author: chenxy
"""

# -*- coding: utf-8 -*-
"""
Created on Sat Dec 31 12:53:10 2022

@author: chenxy
"""

import random
from collections import deque
import time
import itertools

win_comb  = ((0,1,2),(3,4,5),(6,7,8),(0,3,6),(1,4,7),(2,5,8),(0,4,8),(2,4,6))
path_list = [] # used to hold all the possible paths.
path_cnt  = 0
dfs_cnt   = 0

def is_endofgame(s):

def find_neighbor(s):

def print_board(s):

def dfs(path):
    global path_list
    global path_cnt
    global dfs_cnt
    
    dfs_cnt = dfs_cnt + 1
    # if dfs_cnt < 10: # for debug
        # print('dfs_cnt = {0}: path = {1}'.format(dfs_cnt,path))
    
    s = path[-1]
    neighbors = find_neighbor(s)

    for neighbor in neighbors:
        if neighbor not in path:
            
            ## This segment is wrong!
            # path.append(neighbor)
            # end_flag, winner = is_endofgame(neighbor)
            # if end_flag:
            #     path_list.append(path)
            #     path_cnt = path_cnt + 1
            #     if path_cnt < 10:
            #         # print('path_cnt = {0}, path = {1}, len(path_list) = {2}'.format(path_cnt,path,len(path_list)))
            #         print('path_cnt = {0}, path = {1}, path_list = {2}'.format(path_cnt,path,path_list))
            # else:
            #     dfs(path)
            # path.pop() # pop-out the last added node to return to the upper layer

            end_flag, winner = is_endofgame(neighbor)
            if end_flag:
                # path_list.append(tuple([path,winner]))
                path_list.append(path + [neighbor])
                path_cnt = path_cnt + 1
                # if path_cnt < 10: # for debug
                    # print('path_cnt = {0}, path = {1}, path_list = {2}'.format(path_cnt,path,path_list))
            else:
                dfs(path + [neighbor])

    # return path_list

if __name__ == '__main__':

    # Initialization
    s0     = tuple([0] * 9)
    path   = [s0]
    tStart = time.time()
    dfs(path)
    tStop  = time.time()
    
    state_set = set()
    # state_list = []
    # for path in path_list:
    for k in range(path_cnt):
        path = path_list[k]
        # print('k = {0}, path = {1}'.format(k,path))
        for s in path:
            state_set.add(s)
    # state_list = list(itertools.chain(*path_list))
    
    print('Totally there are {0} games'.format(len(path_list)))
    print('Totally there are {0} board states'.format(len(state_set)))
    print('Time cost:  {0:6.2f} seconds'.format(tStop-tStart))

is_endofgame(s)，find_neighbor(s)，print_board(s)等三个函数的代码参见上一篇。

运行结果：

Totally there are 255168 games
Totally there are 5478 board states

也就是说，总共有255168中棋局，但是可能的盘面状态数要少得多，只有5478种状态。

其中，几种可能的棋局如下所示（调用print_board可以打印出更容易看的盘面状态变化图）：

path_list = [

[(0, 0, 0, 0, 0, 0, 0, 0, 0), (0, 0, 0, 0, 0, 0, 0, 0, 1), (0, 0, 0, 0, 0, 0, 0, 2, 1), (0, 0, 0, 0, 0, 0, 1, 2, 1), (0, 0, 0, 0, 0, 2, 1, 2, 1), (0, 0, 0, 0, 1, 2, 1, 2, 1), (0, 0, 0, 2, 1, 2, 1, 2, 1), (0, 0, 1, 2, 1, 2, 1, 2, 1)],

[(0, 0, 0, 0, 0, 0, 0, 0, 0), (0, 0, 0, 0, 0, 0, 0, 0, 1), (0, 0, 0, 0, 0, 0, 0, 2, 1), (0, 0, 0, 0, 0, 0, 1, 2, 1), (0, 0, 0, 0, 0, 2, 1, 2, 1), (0, 0, 0, 0, 1, 2, 1, 2, 1), (0, 0, 0, 2, 1, 2, 1, 2, 1), (0, 1, 0, 2, 1, 2, 1, 2, 1), (0, 1, 2, 2, 1, 2, 1, 2, 1), (1, 1, 2, 2, 1, 2, 1, 2, 1)],

[(0, 0, 0, 0, 0, 0, 0, 0, 0), (0, 0, 0, 0, 0, 0, 0, 0, 1), (0, 0, 0, 0, 0, 0, 0, 2, 1), (0, 0, 0, 0, 0, 0, 1, 2, 1), (0, 0, 0, 0, 0, 2, 1, 2, 1), (0, 0, 0, 0, 1, 2, 1, 2, 1), (0, 0, 0, 2, 1, 2, 1, 2, 1), (0, 1, 0, 2, 1, 2, 1, 2, 1), (2, 1, 0, 2, 1, 2, 1, 2, 1), (2, 1, 1, 2, 1, 2, 1, 2, 1)],

[(0, 0, 0, 0, 0, 0, 0, 0, 0), (0, 0, 0, 0, 0, 0, 0, 0, 1), (0, 0, 0, 0, 0, 0, 0, 2, 1), (0, 0, 0, 0, 0, 0, 1, 2, 1), (0, 0, 0, 0, 0, 2, 1, 2, 1), (0, 0, 0, 0, 1, 2, 1, 2, 1), (0, 0, 0, 2, 1, 2, 1, 2, 1), (1, 0, 0, 2, 1, 2, 1, 2, 1)]]

4. 一个思考题：代码实现中的一个坑

前面说了算法流程（伪代码描述）留了一个坑。这个坑把我坑惨了，花了两个小时才终于看明白咋回事。

一上来按照算法流程的描述，在dfs()函数里面是如下实现的：

## This segment is wrong!
# path.append(neighbor)
# end_flag, winner = is_endofgame(neighbor)
# if end_flag:
# path_list.append(path)
# path_cnt = path_cnt + 1
# if path_cnt < 10:
# # print('path_cnt = {0}, path = {1}, len(path_list) = {2}'.format(path_cnt,path,len(path_list)))
# print('path_cnt = {0}, path = {1}, path_list = {2}'.format(path_cnt,path,path_list))
# else:
# dfs(path)
# path.pop() # pop-out the last added node to return to the upper layer

然后，运行结果始终是不对的。。。经过了两个小时的奋斗，终于想明白了这个问题^-^。这里先不解开谜底。有兴趣的小伙伴可以自己那这段错误的代码运行一下然后看看能不能想明白它为什么错了。