🧸🧸🧸各位大佬大家好,我是猪皮兄弟🧸🧸🧸

文章目录
- 一、最长公共子序列
- 二、两个字符串的删除操作
- 三、编辑距离Hard
为了更好的理解,我们从易到难的来解决编辑距离的问题
一、最长公共子序列
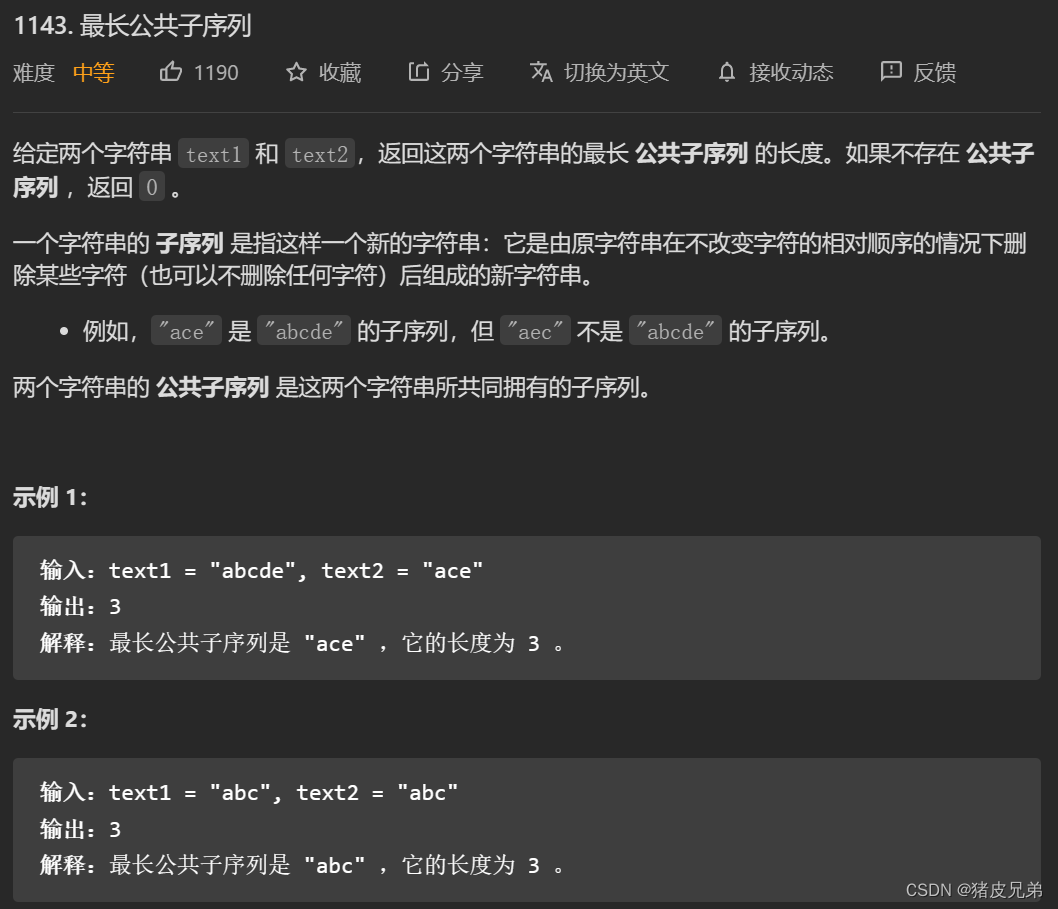
Leetcode最长公共子序列
一般的,我们在做序列DP问题的时候,遇到两个字符串都会用一个二维数组来进行DP,最长公共子序列简称LCS(longest common subsequence)
对于本题
状态定义:
DP[i][j]表示具有word1[0:i]的字符串和word2[0:j]的字符串中的LCS
比如"abcde" [0:2]也就是abc
状态转移方程:
①当word1[i-1]==word2[j-1]
(因为二维DP中dp[i][0]dp[0][j]代表某个字符串为空,所以要多留一个空间的位置,也就是说dp中的i也就是word中的i-1;或者也可以word1=“”+word1,多一个位置)
那么此时就要从之前的LCS的长度+1
dp[i][j]=dp[i-1][j-1]+1
②当word1[i-1]!=word2[j-1]
此时,就需要找之前的最大公共子序列长度
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
(其实这里容易想到还有一个dp[i-1][j-1],但是此位置已经被找过,再加上的话就多余了,虽然加上没什么问题)
初始化:
当某个字符串为空的时候,LCS=0;
dp[i][0]和dp[0][j]都是0
int longestCommonSubsequence(string text1, string text2) {
//dp[i][j] 表示的是当前下的最大公共子序列长度
//text1[0:i]表示text1的0~i这个长度的子串
text1=" "+text1;
text2=" "+text2;
int m = text1.size(),n=text2.size();
vector<vector<int>> dp(m+1,vector<int>(n+1,0));
//dp[0][j]表示空串与text2的子序列,为0 dp[i][0]同理
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
if(text1[i]==text2[j])//两个相等,则最长子序列+1
{
dp[i+1][j+1] = dp[i][j] +1;
}
else //不等则是取其中的最大值,因为dp[i][j]表示到此为止的最大子序列
{
dp[i+1][j+1] = max(dp[i+1][j],dp[i][j+1]);
}
}
}
return dp[m][n];
}
二、两个字符串的删除操作
其实编辑距离就是该题的延伸,所以这道题其实是很重要的
Leetcode两个字符串的删除操作
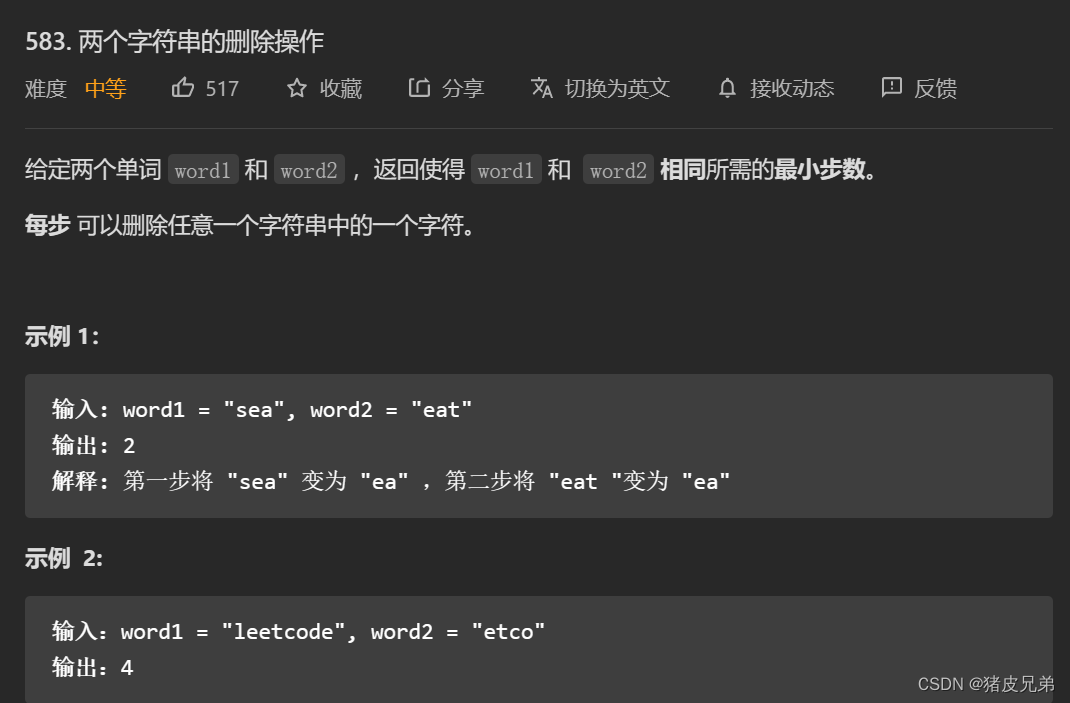
思路一:
我们可以转换为求LCS,然后因为这道题只允许删除,所以返回每个字符串的长度和LCS的差值就可以了
int minDistance(string word1, string word2) {
int m =word1.size();
int n=word2.size();
//最长子序列长度
vector<vector<int>> dp(m+1,vector<int>(n+1,0));
//dp的i就是word的i-1
for(int i=1;i<m+1;i++)
{
for(int j=1;j<n+1;j++)
{
if(word1[i-1]==word2[j-1])
{
dp[i][j]=dp[i-1][j-1]+1;
}
else
{
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
}
return m-dp[m][n]+n-dp[m][n];
}
思路二:
状态定义:
dp[i][j]表示word1[0:i]和word2[0:j]两个字符串的最少删除数
状态转移方程:
提示:因为二维的DP数组会有多的一个判断空字符串的行和列,所以word中的i-1就是dp中的i
①word1[i-1]==word2[j-1]
那么不需要删除
dp[i][j]=dp[i-1][j-1];
②word1[i-1]!=word2[j-1]
那么就需要删除
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+1;
因为比我少一个字符的字符串的最少删除次数以及确定了,我再+1即可
初始化:
当某个字符串为空时 ,删除次数就等于不为空的字符串长度
dp[i][0]=i;
dp[0][j]=j;
int minDistance(string word1, string word2) {
int m =word1.size();
int n=word2.size();
vector<vector<int>> dp(m+1,vector<int>(n+1,0));
for(int i=0;i<m+1;i++) dp[i][0]=i;
for(int j=0;i<n+1;i++) dp[0][j]=j;
for(int i=1;i<m+1;i++)
{
for(int j=1;j<n+1;j++)
{
if(word1[i-1]==word2[j-1])
{
dp[i][j]=dp[i-1][j-1];
}
else
{
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+1;
}
}
}
return dp[m][n];
}
三、编辑距离Hard
Leetcode编辑距离
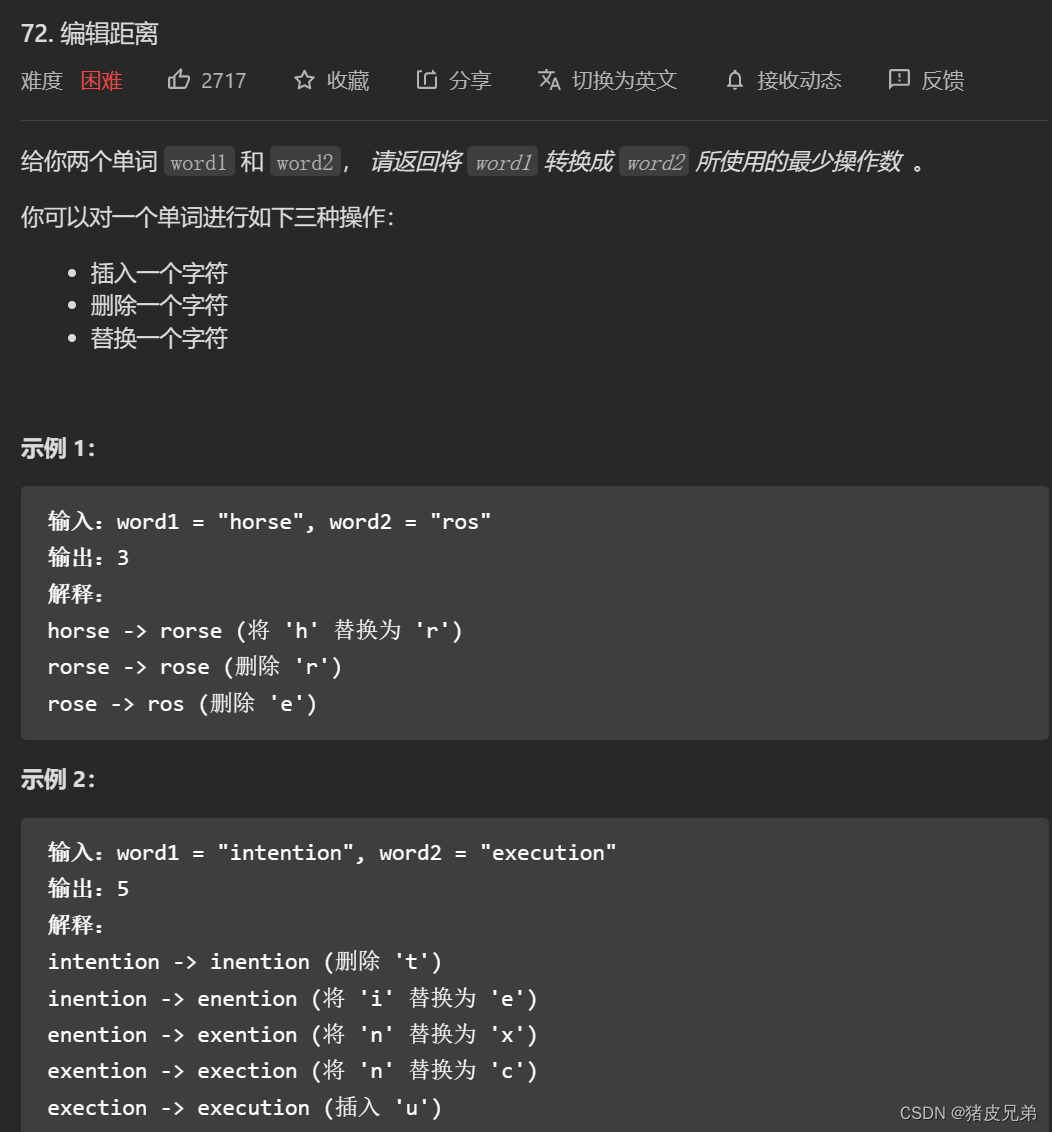
其实最难的就是dp的定义,dp数组中的值代表什么意思,然后分析好有什么情况,写出状态转移方程基本上就做出来了
状态定义:
dp[i][j]表示word1[0:i]和word2[0:j]这两个字符串的最少编辑次数
状态转移方程:
通过分析,我们发现每个字符串有三种操作 插入/删除/替换
那么,对于两个字符串 A B 就有六种操作
但是,很快发现:
1.对于A的插入其实就相当于对于B的删除
比如A:dog B:doge
2.对于A的删除其实就相当于对于B的插入
比如A:doge B:dog
3.对于A的替换和对于B的替换是等价的
所以我们分析出
①当word1[i-1]==word2[j-1]
那么此时我们不需要进行操作
dp[i][j]=dp[i-1][j-1];
②当word1[i-1]!=word2[j-1]
那么此时就有三种可能
第一种:对A插入/对B删除
第二种:对A删除/对B插入
第三种:对A替换/对B替换
dp[i][j]=max({dp[i][j-1],dp[i-1][j],dp[i-1][j-1]})+1
dp[i-1][j]就表示对A进行插入/对B删除,因为A少一个
同理dp[i][j-1]也是一样
dp[i-1][j-1]表示替换,因为你必须是同时增加一个字符才是替换,不然的话长度不对,只能是在上一个的基础上插入或者删除
初始化:
当有一个串为空串,那么
dp[i][0]=i ;
dp[0][j]=j ;
int minDistance(string word1, string word2) {
//序列dp的套路,两个字符串一般用二维dp
int m = word1.size();
int n=word2.size();
vector<vector<int>> dp(m+1,vector<int>(n+1,0));//多开一个的原因是dp[i][0]和dp[0][j]有一个串是空串
for(int i=0;i<m+1;i++)
dp[i][0]=i;
for(int j=0;j<n+1;j++)
dp[0][j]=j;
//初始化两个串某一个为空的操作
for(int i=1;i<m+1;i++)
{
for(int j=1;j<n+1;j++)
{
if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];//多一个字符串的话肯定要做修改
else
{
dp[i][j]=min({dp[i-1][j-1],dp[i-1][j],dp[i][j-1]})+1;
}
}
}
return dp[m][n];
}