基础数学（五）——数值积分

news2024/9/23 9:24:00

文章目录

        • 考试要求
        • 基础概念
        • 代数精度（必考题）
          • 代数精度的定义
          • 求代数精度的例题（期末考试数值积分第一个大题）
        • 数值积分公式的构造
          • 插值型求积公式（必考题）
            • 插值型数值积分公式定理
            • Newton-Cotes求积公式
            • Cotes公式代数精度（必考）
        • Cotes公式例题（必考）
          • 梯形公式
          • Simpson公式
          • 例题（必考）
        • 改进的N-C公式
          • N-C公式缺点
          • 复化求积公式
            • 复化梯形公式
            • 复化Simpson公式
          • 复化公式计算样例（有可能会考）
          • 自适应步长求积法
            • Richardson加速外推
            • 例题计算（必考）
        • 高斯型的求积公式
          • Legendre多项式（勒让德多项式）（必考，仅仅考两阶）
          • 必考题（求[a,b]上的Gauss型求积公式，二阶）
        • 计算定积分，使用不同的方法进行计算
        • 积分公式的总结
          • 考试要求

考试要求

  • 给你不完整的数值积分公式，把他凑完整，找尽可能高的代数精度使其完整。
  • 要能够判定其对应代数精度。
  • 随便给的定积分，要用梯形公式或者辛普森公式计算，并计算对应有效数字
  • 能够根据对应要求，确定需要几个等分点。
  • 高斯型求积公式，仅仅考两个点的

基础概念

  • 使用被积函数在某些点的函数值的乘积的累加和，积分的近似值。
    在这里插入图片描述
  • 两个基本问题：
    • 构造：选取求积节点Xi、求积系数Ai
    • 分析：衡量精度
  • 根据积分中值定理，可以使用一个点的积分，去成功获取对应积分结果
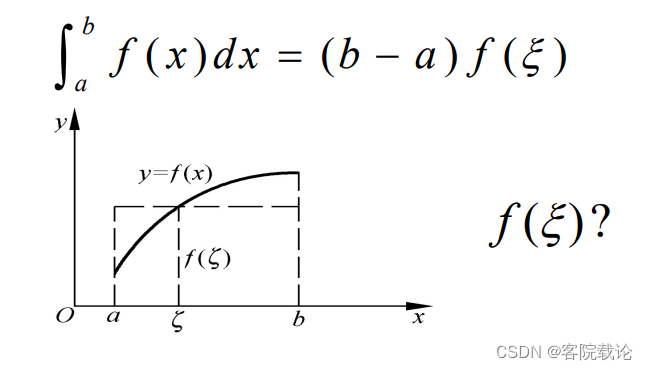
    在这里插入图片描述
  • 衡量数值积分公式好坏的标准
    • 误差：
      • 计算实际积分和数值积分误差，通过误差来衡量。但是实际积分的结果计算不出来。
    • 公式精确成立的范围
      • 数值积分公式所适用的范围越大，越好。左矩形公式就只适用于常函数，中矩形公式使用常函数和一次函数等。
        在这里插入图片描述

代数精度（必考题）

代数精度的定义

在这里插入图片描述

  • 证明方法：
    • 依次带入1，x，x²，x³等进行判定
求代数精度的例题（期末考试数值积分第一个大题）

在这里插入图片描述

  • 求三个待定系数，需要找其满足的条件。在尽可能高的代数精度，顺次选择不同的精度进行假设，设定对应的方程。
    在这里插入图片描述
  • 方法
    • 从低次到高次，顺次假设对应的方程，然后计算出对应的方程组进行假设。
    • 若线性方程组无解，需要顺次减少最高次的方程，知道满足为止。
    • 若线性方程组解存在，且不为唯一，那就继续增加对应的限制条件。
    • 注意：一定要计算出不成立的次数为止。

数值积分公式的构造

插值型求积公式（必考题）

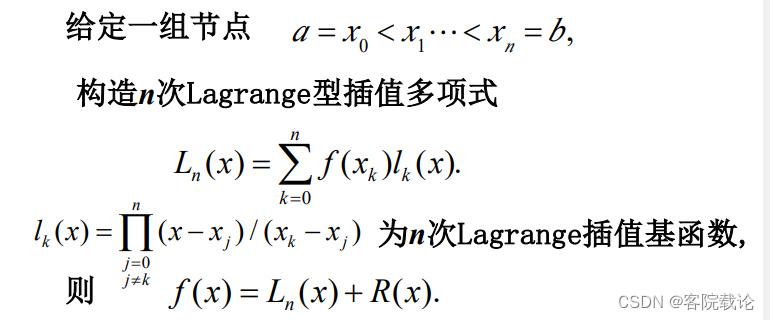
在这里插入图片描述
在这里插入图片描述

插值型数值积分公式定理

在这里插入图片描述

Newton-Cotes求积公式
  • 特点：Cotes 将求积系数分为和ab区间有关和无关两个部分。
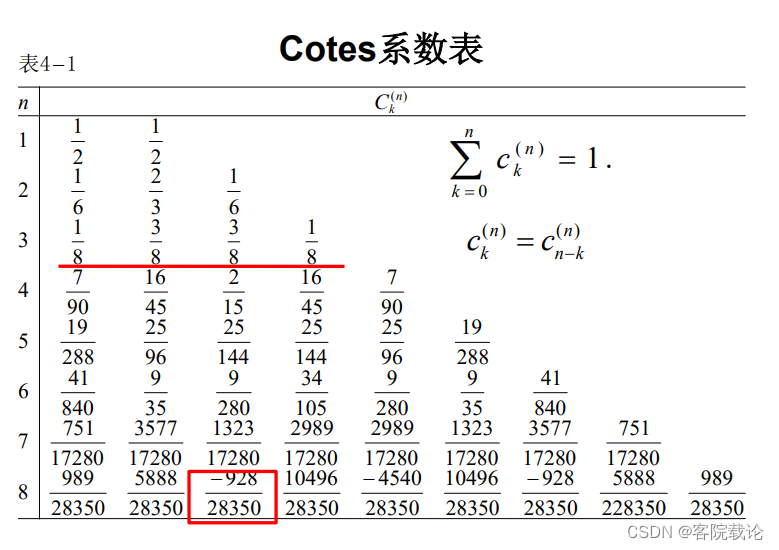
    在这里插入图片描述在这里插入图片描述

在这里插入图片描述

  • Cotes的特点
    • 最低阶的cotes公式是两个点的，所有cotes公式代数精度都是大于等于一次。
      在这里插入图片描述
Cotes公式代数精度（必考）

在这里插入图片描述

  • 这里n是等分数，n个点，等分数就是n-1.六个等分点，就是五阶，代数精度就是五次。
    在这里插入图片描述

  • 五次函数，至少需要五次代数精度，所以最少需要四阶n-c公式

Cotes公式例题（必考）

梯形公式

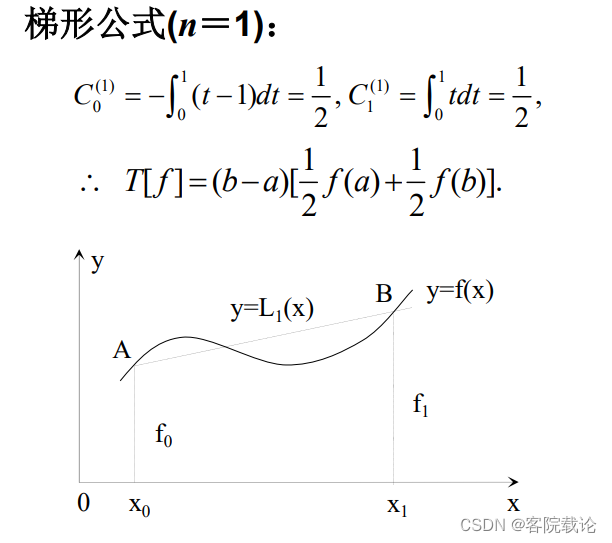
在这里插入图片描述

  • 推导
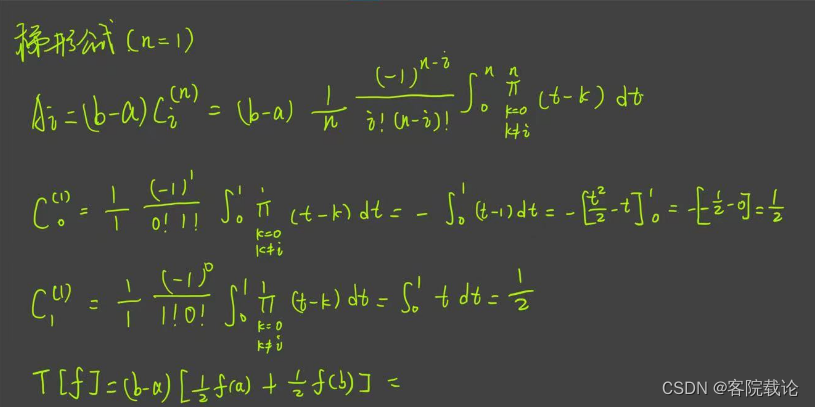
    在这里插入图片描述

  • 截断误差
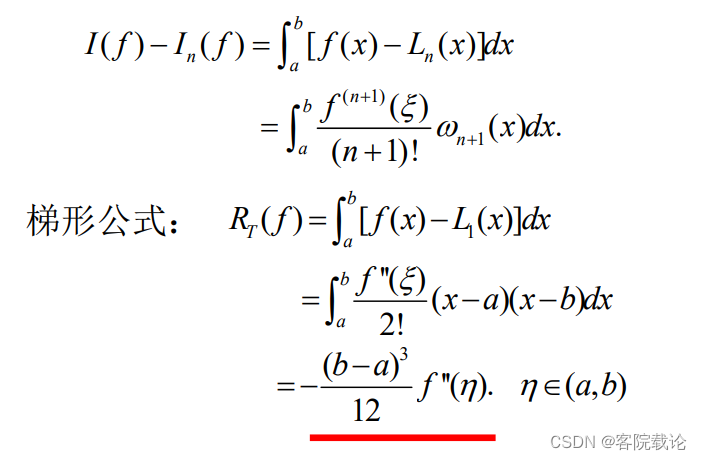
    在这里插入图片描述

  • 代数精度
    在这里插入图片描述

Simpson公式

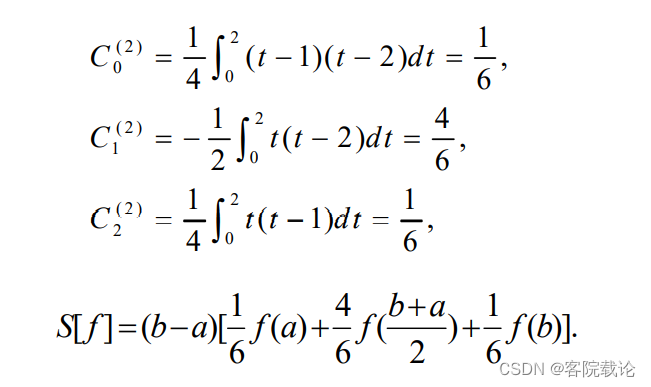
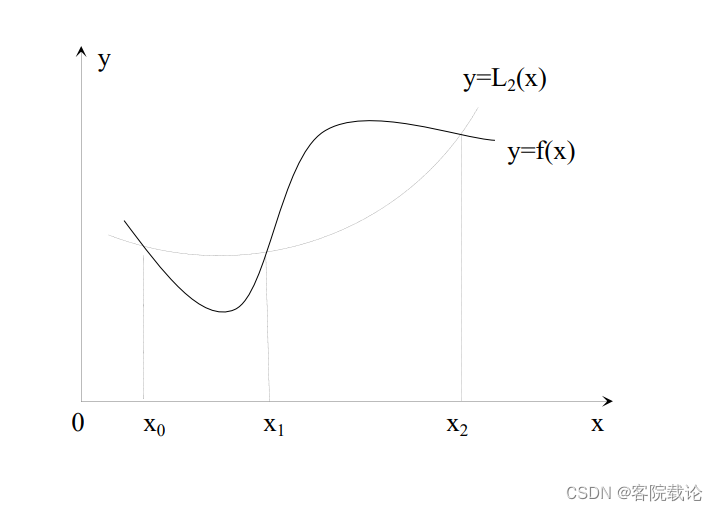
在这里插入图片描述

在这里插入图片描述

  • 代数精度

在这里插入图片描述

  • 截断误差

在这里插入图片描述

例题（必考）
  • 考试要求：随便给一个定积分，用梯形公式或者simpson公式计算一次
    在这里插入图片描述

改进的N-C公式

N-C公式缺点
  • 高阶N-C公式不稳定，会放大误差
    在这里插入图片描述
    在这里插入图片描述
复化求积公式
  • 本质：用分段线性插值近似被积函数
复化梯形公式

在这里插入图片描述

  • 左右两端端点都用了一次，区间内的n-1点，用了两次。
    在这里插入图片描述
  • 用了n+1个点
复化Simpson公式

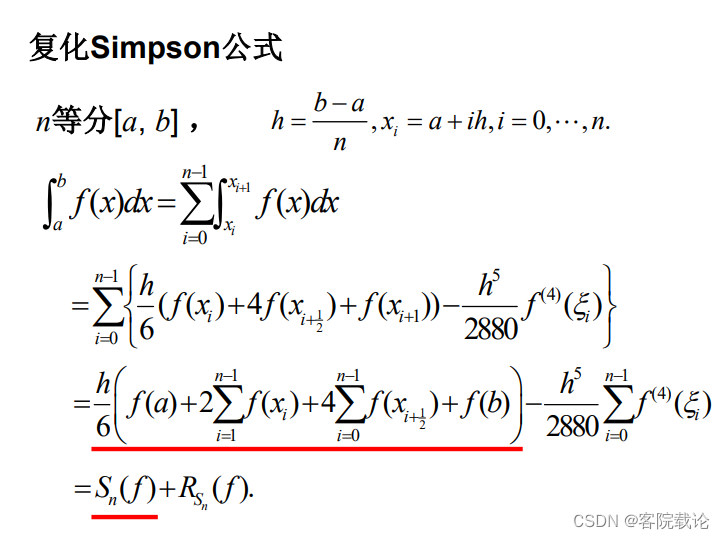
在这里插入图片描述

  • 用了2n+1个点
    在这里插入图片描述
  • 只能用收敛阶来衡量收敛速度。
  • 复化辛普森公式需要导数四阶连续，复化梯形公式需要导师二阶连续
复化公式计算样例（有可能会考）

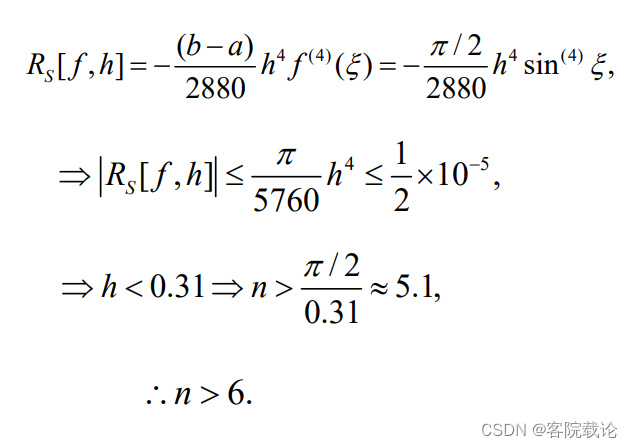
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

自适应步长求积法
  • 通过后验误差的来判定先验误差，从而实现对误差的判定，决定是否还要在进行加密划分。
    在这里插入图片描述
    在这里插入图片描述
Richardson加速外推
  • 复化梯形公式加速外推，变为复化Simpson公式，实现代数精度的进一步提高。
    在这里插入图片描述
  • 复化Simpson公式进一步外推，变为复化Cotes公式，进一步提高精度，减少误差
    在这里插入图片描述
  • Romberg公式
    在这里插入图片描述
例题计算（必考）
  • 能够根据误差要求，确定对应划分的阶数
    在这里插入图片描述
    在这里插入图片描述

高斯型的求积公式

  • 在代数精度意义下，理论上最优的求积公式
    在这里插入图片描述
  • 高斯点的充分必要条件
    • 求积节点的充分必要条件是，以求积节点为零点的n+1次多项式，和任何一个不超过n次的多项式，相乘之后求定积分都为零。正交多项式的零点，就是最优的高斯多项式的结果。
  • 注意，这里是n+1个点，进行分类的
    在这里插入图片描述
Legendre多项式（勒让德多项式）（必考，仅仅考两阶）

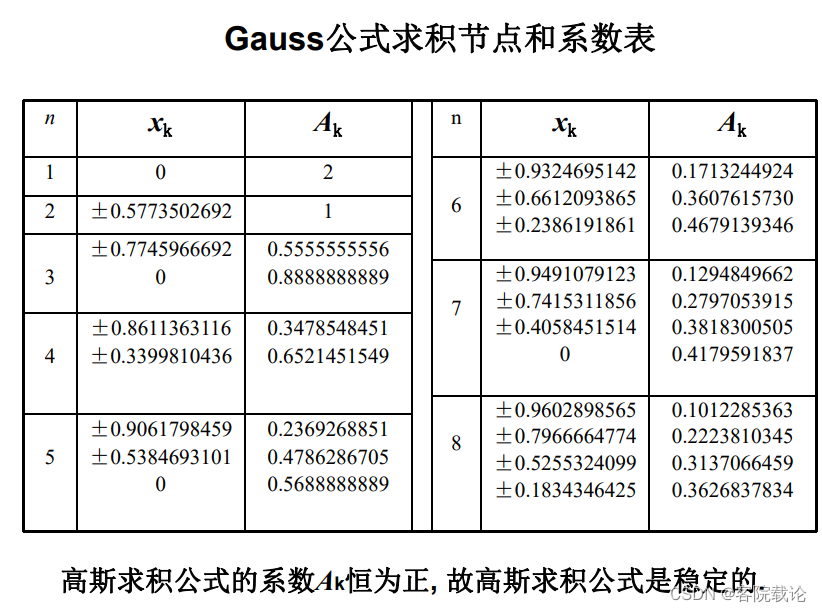
在这里插入图片描述

  • 具体推导
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
必考题（求[a,b]上的Gauss型求积公式，二阶）
  • 线性替换，这里要会，将区间变为[-1,1]
    在这里插入图片描述
    在这里插入图片描述
  • 注意：这里仅仅考两个点的高斯公式

计算定积分，使用不同的方法进行计算

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

  • 不会单纯使用复化梯形公式，还要使用Romberg积分进行外推，尽量少的计算量的情况下，获取更高的精度

积分公式的总结

在这里插入图片描述

考试要求
  • 不完整的积分公式，在保证尽可能高精度的情况下，将其补充完整。同时会验证你构造的数值公式
  • 随便给你一个定积分，要会使用特定的方法进行计算，romberg不考，仅仅考两个点的复化梯形公式。高斯公式仅仅考两个点的高斯公式，要回计算有效数字。两个点的高斯公式要会计算，算不出来就不算，只要把计算过程写出来就行了。
  • 对于刚才算的定积分，你用cotes公式，高斯公式，分别需要几个点。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/132368.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

webpack 学习

webpack 学习

1.拆分、合并 webpack-merge devlopment production 2.webpack-dev-serve devServer: { port contentBase progress open compress proxy:{ xxx:{ target:..., pathRewrite:{ "^/api" }, changeOrigin:true } } } 3.处理样式 css module:{ rules:[ { test:/\.sc…
阅读更多...
qt开关控件设计（手把手从零开始）

qt开关控件设计（手把手从零开始）

从零开始手把手教你设计自己的qt控件1 说明1.1 显示效果1.2 控件特性1.3 设计方法2 控件需求分析2.1 必要需求2.1 顺带需求（锦上添花）3 功能设计3.1 设计思路（重点内容）3.2 自适应大小3.3 开关动画3.4 控件绘制4 总体代码1 说明 …
阅读更多...
推动新能源越野场景革命 坦克品牌开创越野新生态

推动新能源越野场景革命 坦克品牌开创越野新生态

近日，坦克品牌以“创领越野新生态”为主题，携多款车型登陆第二十届广州国际汽车展览会。秉持“以用户为中心”，坦克品牌围绕技术与生态双线出击，正式亮相坦克500 PHEV长续航版、生活方式共创平台TANK Life。技术创领，打…
阅读更多...
docker-ui创建使用

docker-ui创建使用

首先需要安装docker: apt install docker.io composer也需要安装： apt install composer docker查找docker-ui镜像： docker search docker-ui 在列表里选一个镜这里就选第一个。 docker pull builtdock/docker-ui 然后直接docker run 使用的时候&#x…
阅读更多...
DSL操作ElasticSearch基础命令

DSL操作ElasticSearch基础命令

文章目录一、DSL操作ES-RESTful风格二、DSL操作索引库2.1 PUT 添加索引2.2 GET 查询索引2.3 DELETE 删除索引2.4 POST 打开/关闭索引库三、DSL操作映射3.1 数据类型3.1.1 简单数据类型3.1.2 复杂数据类型3.2 创建索引库并设置映射3.2.1 语法格式3.2.2 举例3.3 查询索引库映射3.…
阅读更多...
python中的类型注解

python中的类型注解

目录 一.类型注解 变量的类型注解 类型注解的语法 类型注解主要功能在于: 函数方法的类型注解 函数（方法）形参进行类型注解 函数（方法）返回值进行类型注解 小结 Union类型 小结 一.类型注解 变量的类型注解 思考 为什么…
阅读更多...
Android美团多渠道打包Walle集成

Android美团多渠道打包Walle集成

一、为什么使用美团多渠道打包的方式？ 打包更加快速 传统的通过productFlavors渠道包的方式，渠道10个以内还可以接受，如果100个渠道包，每个包需要打5Min,就是将近10个小时的打包，而采用美团Walle多渠道打包的方式只需…
阅读更多...
PyTorch 2.0 推理速度测试：与 TensorRT 、ONNX Runtime 进行对比

PyTorch 2.0 推理速度测试：与 TensorRT 、ONNX Runtime 进行对比

PyTorch 2.0 于 2022 年 12 月上旬在 NeurIPS 2022 上发布，它新增的 torch.compile 组件引起了广泛关注，因为该组件声称比 PyTorch 的先前版本带来更大的计算速度提升。 这对我们来说是一个好消息，训练时间改进的结果令人印象深刻。PyTorch 团…
阅读更多...
JavaScript 入门基础 - 流程控制（四）

JavaScript 入门基础 - 流程控制（四）

JavaScript 流程控制 - 分支和循环 文章目录JavaScript 流程控制 - 分支和循环1. 什么是流程控制2. 顺序流程控制3. 分支流程控制 之 if语句3.1 什么是分支结构3.2 if 语句3.2.1 if 语句基本理解3.2.2 if 语句执行流程3.2.3 if 语句案例3.3 if else语句（双分支语句&…
阅读更多...
Threejs实现鼠标点击人物行走/镜头跟随人物移动/鼠标点击动画/游戏第三人称/行走动作

Threejs实现鼠标点击人物行走/镜头跟随人物移动/鼠标点击动画/游戏第三人称/行走动作

1，功能介绍 Threejs获取鼠标点击位置、实现鼠标点击人物行走、人物头顶显示名称标签、镜头跟随人物移动并且镜头围绕人物旋转，类似游戏中第三人称、鼠标点击位置有动画效果，如下效果图 2，功能实现 获取鼠标点击位置，…
阅读更多...
【Linux】进程间通信 - 匿名/命名管道与System V共享内存

【Linux】进程间通信 - 匿名/命名管道与System V共享内存

目录 前言 一.管道 0.什么是管道 1).管道的概念 2).管道的本质 3).管道指令: "|" 1.匿名管道 1).如何创建匿名管道 2).如何使用匿名管道进行通信 3).匿名管道的特点总结 2.命名管道 0).指令级的命名管道的通信 1).如何在编程时创建命名管道 2).如何在…
阅读更多...
你好2023-使用msys64 openssl 制作QSslSocket实验所需证书

你好2023-使用msys64 openssl 制作QSslSocket实验所需证书

2023年开始了，第一篇，记录最近帮朋友制作QSslSocket所需证书的过程。 使用传统的TCP连接依旧是很多工业软件的常见通信方法。但如果恰好不希望别人通过抓包等方法研究上位机和控制器模块之间的协议格式，那使用SSL连接是一种掩耳盗铃的好办法&…
阅读更多...
Pyinstaller - 你的“神”队友

Pyinstaller - 你的“神”队友

哈哈！今天是我在2023年发布的第一篇文章呀！ 这两天，我在做一个爬虫项目。因为我做好后准备给我的朋友看看，但我朋友没有 Python 环境。所以，只好想办法把 .py 打包成 .exe 。 在网上搜了一下，发现目前相对…
阅读更多...
设计模式 ——工厂模式

设计模式 ——工厂模式

前言 有一些重要的设计原则在开篇和大家分享下，这些原则将贯通全文： 面向接口编程，而不是面向实现。这个很重要，也是优雅的、可扩展的代码的第一步，这就不需要多说了吧。 职责单一原则。每个类都应该只有一个单一的功…
阅读更多...
第三十一讲：神州路由器策略路由的配置

第三十一讲：神州路由器策略路由的配置

从局域网去往广域网的流量有时需要进行分流，即区别了不同用户又进行了负载分担，有时这种目标是通过对不同的源地址进行区别对待完成的，通过策略路由的方法可以解决此问题。 实验拓扑图如下所示 R1 R2 R3 F0/0 1.1.3.1/24 F0/0 1.1.3.2…
阅读更多...
【AcWing每日一题】4261. 孤独的照片

【AcWing每日一题】4261. 孤独的照片

Farmer John 最近购入了 N 头新的奶牛，每头奶牛的品种是更赛牛（Guernsey）或荷斯坦牛（Holstein）之一。 奶牛目前排成一排，Farmer John 想要为每个连续不少于三头奶牛的序列拍摄一张照片。 然而&#xff0c…
阅读更多...
java多线程（11）：线程协作

java多线程（11）：线程协作

1 线程通信 应用场景 : 生产者和消费者问题 假设仓库中只能存放一件产品 , 生产者将生产出来的产品放入仓库 , 消费者将仓库中产品取走消费 如果仓库中没有产品 , 则生产者将产品放入仓库 , 否则停止生产并等待 , 直到仓库中的产品被消费者取走为止 如果仓库中放有产品 ,…
阅读更多...
Chrome Extension 基础篇

Chrome Extension 基础篇

Extensions are software programs, built on web technologies (such as HTML, CSS, and JavaScript) that enable users to customize the Chrome browsing experience. 扩展程序是基于 Web 技术（例如 HTML、CSS 和 JavaScript）构建的软件程序&#xf…
阅读更多...
C语言递归

C语言递归

递归指的是在函数的定义中使用函数自身的方法。 举个例子： 从前有座山，山里有座庙，庙里有个老和尚，正在给小和尚讲故事呢！故事是什么呢？"从前有座山，山里有座庙，庙里有个老和尚…
阅读更多...
redis的安装

redis的安装

1.Redis是基于C语言编写的，因此首先需要安装Redis所需要的gcc依赖： yum install -y gcc tcl2.上传安装包并解压 tar -xzf redis-6.2.6.tar.gz3.解压后，进入redis目录 cd redis-6.2.64.运行编译命令 make && make install如果没有…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023