这篇笔记记录分治算法的思想和两道leetcode题。

分治算法思想：

规模为n的原问题的解无法直接求出，进行问题规模缩减，划分子问题，子问题相互独立而且和原问题解的性质是相同的，只是问题规模缩小了。递归地缩小问题规模，直到能求出解为止。最后将求出的小规模的问题的解合并为一个更大规模问题的解，自低向上逐步求出原问题的解。

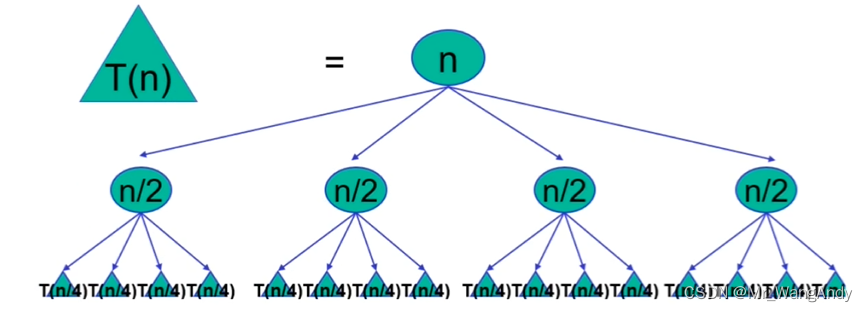
分治算法适用条件

分治法所能解决的问题一般具有以下几个特征：
1.原问题的规模缩小到一定的程度就可以容易地解决;
2. 原问题可以分解为若干规模较小的相同的问题，即原问题具有最优子结构性质；
3. 利用原问题分解出的子问题的解可以合并为原问题的解；
4. 原问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题（这条特征涉及到分治法的效率，如果各个子问题不独立，也就是子问题划分有重合的部分，则分治法要重复的求解公共子问题的解，此时虽然也可用分治法，但采用 动态规划 更好）

分治算法练习题

1 二分搜索

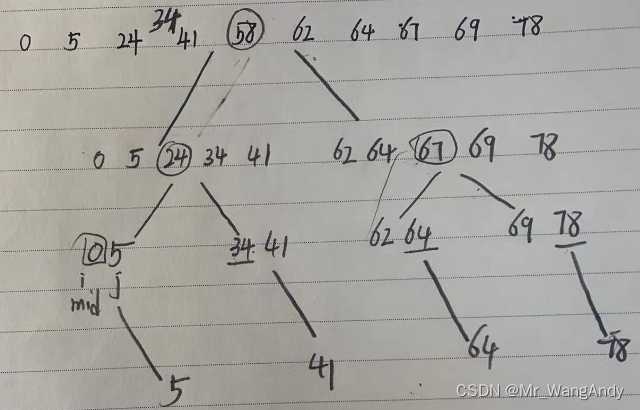
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

bool Binart_search(vector<int> &vec, int i, int j, int val)
{
	
	if (i > j)
	{
		return false;
	}

	int mid = (i + j) / 2;
	if (vec[mid] == val)
	{
		return true;
	}
	else if (vec[mid] > val)
	{
		return Binart_search(vec, i, mid-1, val);
	}
	else
	{
		return Binart_search(vec, mid + 1, j, val);
	}
}


int main()
{
	vector<int> vec;
	for (int i = 0; i < 11; i++)
	{
		vec.push_back(rand() % 100);
	}
	sort(vec.begin(), vec.end());
	
	for (int v : vec)
	{
		cout << v << " ";
	}
	cout << endl;

	bool  result = Binart_search(vec, 0, vec.size() - 1, 34);
	if (result)
	{
		cout << "result:" << result <<  endl;
	}
	for (int v : vec)
	{
		cout << v << " ";
	}
	cout << endl;
	system("pause");
	return 0;
}

2. 快速排序

int partition(vector<int> &vec, int i, int j)
{
	int val = vec[i];
	int l = i;
	int r = j;

	while (l < r)
	{
		while (l < r && vec[r] >= val)
		{
			r--;
		}
		if (l < r)
		{
			vec[l++] = vec[r];
		}

		while (l < r && vec[l] < val)
		{
			l++;
		}
		if (l < r)
		{
			vec[r--] = vec[l];
		}
	}
	vec[l] = val;
	return l;
}

void quickSork(vector<int> &vec, int i, int j)
{
	if (i >= j)  // 递归结束条件
	{
		return;
	}
	int pos = partition(vec, i, j);
	quickSork(vec, i, pos - 1);
	quickSork(vec, pos + 1, j);

}


int main()
{
	vector<int> vec;
	for (int i = 0; i < 11; i++)
	{
		int r = rand() % 100;
		vec.push_back(r);
		cout << r << " ";
	}
	cout << endl;
	quickSork(vec, 0, vec.size() - 1);
	for (int v : vec)
	{
		cout << v << " ";
	}
	cout << endl;
	system("pause");
	return 0;
}

3. 归并排序

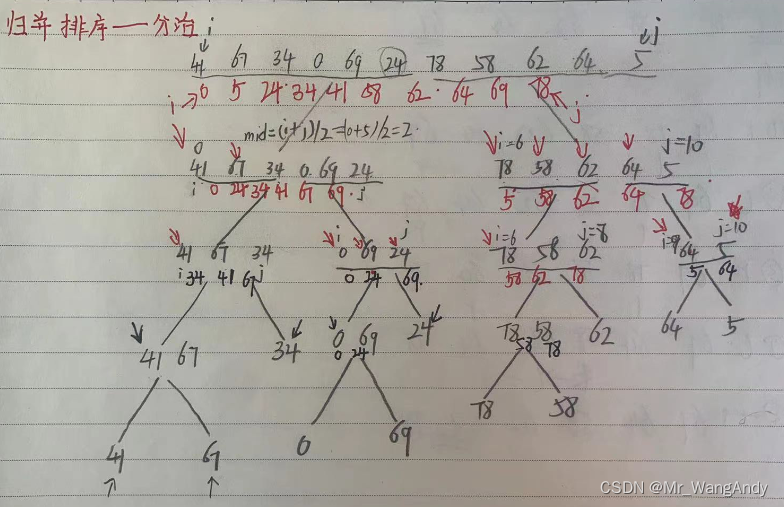
void merge1(vector<int> &vec, int low, int high, int mid)
{
	vector<int> tmp;			// 定义额外的辅助空间，存储合并的子问题的有序数组
	tmp.reserve(high - low + 1);// reserve(预留空间，防止扩容的消耗) resize
	int i = low;
	int j = mid + 1;

	while (i <= mid && j <= high)
	{
		if (vec[i] > vec[j])
		{
			tmp.push_back(vec[j++]);
		}
		else
		{
			tmp.push_back(vec[i++]);
		}
	}
	while (i <= mid)
	{
		tmp.push_back(vec[i++]);
	}

	while (j <= high)
	{
		tmp.push_back(vec[j++]);
	}

	for (int k = low; k <= high; ++k)
	{
		vec[k] = tmp[k - low];
	}
}

void mergeSort(vector<int> &vec, int i, int j)
{
	if (i >= j)
	{
		return;
	}
	int mid = (i + j) / 2;
	mergeSort(vec, i, mid);
	mergeSort(vec, mid + 1, j);// Andy:这两个递归函数，逻辑上将树划分成二叉树

	// 向上回溯，回溯过程中，合并子问题的接
	merge1(vec, i, j, mid);
}

int main()
{
	vector<int> vec;
	for (int i = 0; i < 11; i++)
	{
		int r = rand() % 100;
		vec.push_back(r);
		cout << r << " ";
	}
	cout << endl;
	
	mergeSort(vec, 0, vec.size() - 1);
	for (int v : vec)
	{
		cout << v << " ";
	}
	cout << endl;
	system("pause");
	return 0;
}

4. 快排分割函数求top K问题

求大数据的topk问题，有两种解决方法：
1 大根堆，小根堆，优先级队列
10万个整数， 求值最大的前10个元素，解决方法：最开始的前K个元素，组成一个小根堆，从11-10万个元素比较cur, 如果 top > cur ，说明当前的10个是最大的；如果cur > top, top出堆，然后cur 入堆，最后得到的堆就是topk;
如果求前10个小的，先构建大根堆，堆顶元素值最大，依次比较11-10万个元素，如果cur > top 继续下一个元素；如果cur < top ，那么top出堆让，然后cur入堆；O(logn) * O(log10) = O(n)；
2 快排划分函数
假如找第k大的元素，用Length - k =j ,
如果分割函数返回值pos> j ,说明下一次要从i —pos -1 中找；
如果分割函数返回值pos < j ,说明下一次要从pos + 1—length中找；

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

static int partition(vector<int> &vec, int i, int j)
{
	int val = vec[i];
	int l = i;
	int r = j;

	while (l < r)
	{
		while (l < r && vec[r] >= val)
		{
			r--;
		}
		if (l < r)
		{
			vec[l++] = vec[r];
		}

		while (l < r && vec[l] < val)
		{
			l++;
		}
		if (l < r)
		{
			vec[r--] = vec[l];
		}
	}
	vec[l] = val;
	return l;
}


int max_select_topk(vector<int> &vec, int i, int j, int k)
{
	int pos = partition(vec, i, j);
	if (pos == vec.size() - k)
	{
		return pos;
	}
	else if (pos < vec.size() - k)
	{
		return max_select_topk(vec, pos + 1, j, k);
	}
	else
	{
		return max_select_topk(vec, i, pos - 1, k);
	}

}



int main()
{
	vector<int> vec;
	for (int i = 0; i < 20 ; i++)
	{
		int r = rand() % 100;
		vec.push_back(r);
		cout << r << " ";
	}
	cout << endl;
	int pos = max_select_topk(vec, 0, vec.size() - 1,8);
	for (int i = pos; i < vec.size();++i)
	{
		cout << vec[i] << " ";
	}
	cout << endl;
	system("pause");
	return 0;
}