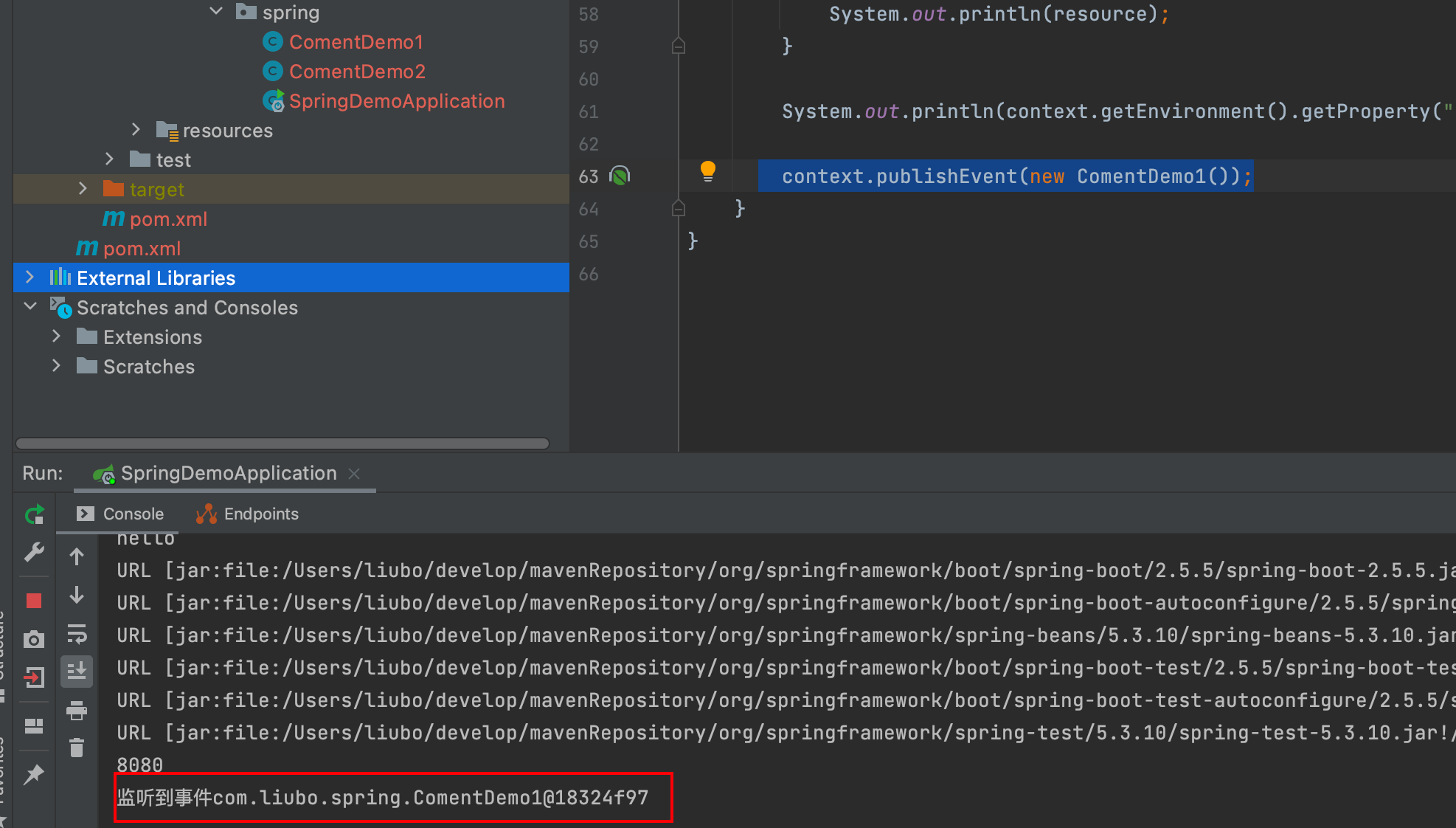
回顾一下非正式的极限定义法。当x从任意一侧(自左向右或自右向左)接近常量 c时，如果f(x)变得任意接近一个单独的值L, 则当x接近c时f(x)的极限值是L, 写作

咋一看，这个定义似乎非常技术化。即使这样，它仍然是非正式的，因为它没有给出两这两个短语的准确意义, 即“f(x)变得任意接近L”和“x接近c。”

给这两个短语赋予数学上严格意义的第一人是Augustin-Louis Cauchy(奥古斯丁.路易斯.柯西, 1789年8月21日-1857年5月23日,法国数学家，简称“柯西”)。它的“ε-δ极限定义法(ε-δ definition of limit)”是今天使用的标准定义法。如下图：

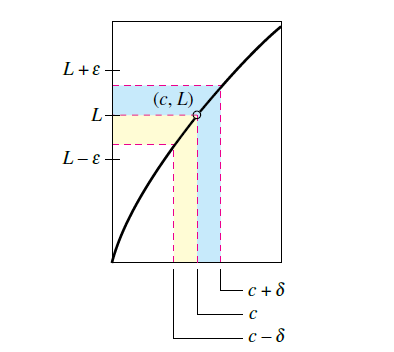
用ε(西腊字母的epsilon的小写形式)表示一个(极小的)正数。则短语“f(x)变得任意接近L”意思就是指f(x)落在开区间(L-ε, L+ ε)中，使用绝对值形式，可以写成

| f(x)- L|<ε 。

类似地，短语“x接近c”指存在一个正数δ，使得x落在开区间(c-δ, c)和(c，c+δ)。实际上，这可以准确地使用双不等式表示

0<| x- c|<δ 。

第一个不等式0<| x- c| (x和c之间的距离大于0) 表达了x≠c这个事实。第二个不等式

| x- c|<δ (x在c的δ单元范围内)是说x在c的δ距离范围内。

因此，正式定义为：

用f 表示定义在包含c(可能除掉c)的开区间上的函数，并使用L表示实数。表达式

指的是，对于任意一个ε>0,都存在一个δ>0，使得只要

0<| x- c|<δ, 则 | f(x)- L|<ε 。

表达式

有两层含义：极限存在，并且等于L。

一些函数在x接近c时没有限制，但是，随着x接近c，绝不可能有两个极限。即，只要函数的极限存在，则其极限必定是唯一的。

参考资料：

<<calculus>> Ron Larson,The Pennsylvania State University The Behrend College
Bruce Edwards, University of Florida