📖 前言:消息认证码 MAC(Message Authentication Code)是经过特定算法后产生的一小段信息,检查某段消息的完整性,以及作身份验证。它可以用来检查在消息传递过程中,其内容是否被更改过,不管更改的原因是来自意外或是蓄意攻击。同时可以作为消息来源的身份验证,确认消息的来源。

目录
- 🕒 0. 思维导图
- 🕒 1. 常见攻击
- 🕒 2. 对消息认证的要求
- 🕒 3. 消息认证函数
- 🕘 3.1 Hash
- 🕘 3.2 加密
- 🕤 3.2.1 对称加密
- 🕞 3.2.1.1 内部错误控制
- 🕞 3.2.1.2 外部错误控制
- 🕤 3.2.2 公钥加密
- 🕞 3.2.2.1 使用公钥PU
- 🕞 3.2.2.2 使用私钥PR
- 🕞 3.2.2.3 公私钥结合
- 🕘 3.3 消息认证码
- 🕤 3.3.1 原始版本
- 🕤 3.3.2 V2.0 版本
- 🕤 3.3.3 V2.1 版本
- 🕒 4. MAC的应用
- 🕘 4.1 作用场景
- 🕘 4.2 实际应用
- 🕤 4.2.1 HMAC
- 🕒 5. 攻击
- 🕘 5.1 加密
- 🕤 5.1.1 穷举攻击
- 🕘 5.2 认证
- 🕤 5.2.1 穷举攻击
- 🕤 5.2.2 伪造攻击
- 🕒 6. 对消息认证码的要求
- 🕘 6.1 抗伪造攻击
- 🕘 6.2 均匀分布
- 🕒 7. 基于Hash函数的MAC——HMAC
- 🕘 7.1 应用
- 🕘 7.2 设计目标
- 🕘 7.3 流程
- 🕘 7.4 执行时间
- 🕘 7.5 设计目标
- 🕒 8. 基于分组密码的MAC
- 🕘 8.1 DAA
- 🕘 8.2 CMAC
- 🕤 8.2.1 消息长度是分组长度的整数倍
- 🕤 8.2.2 消息长度不是分组长度的整数倍
- 🕒 9. 认证加密——CCM
- 🕘 9.1 认证
- 🕘 9.2 加密
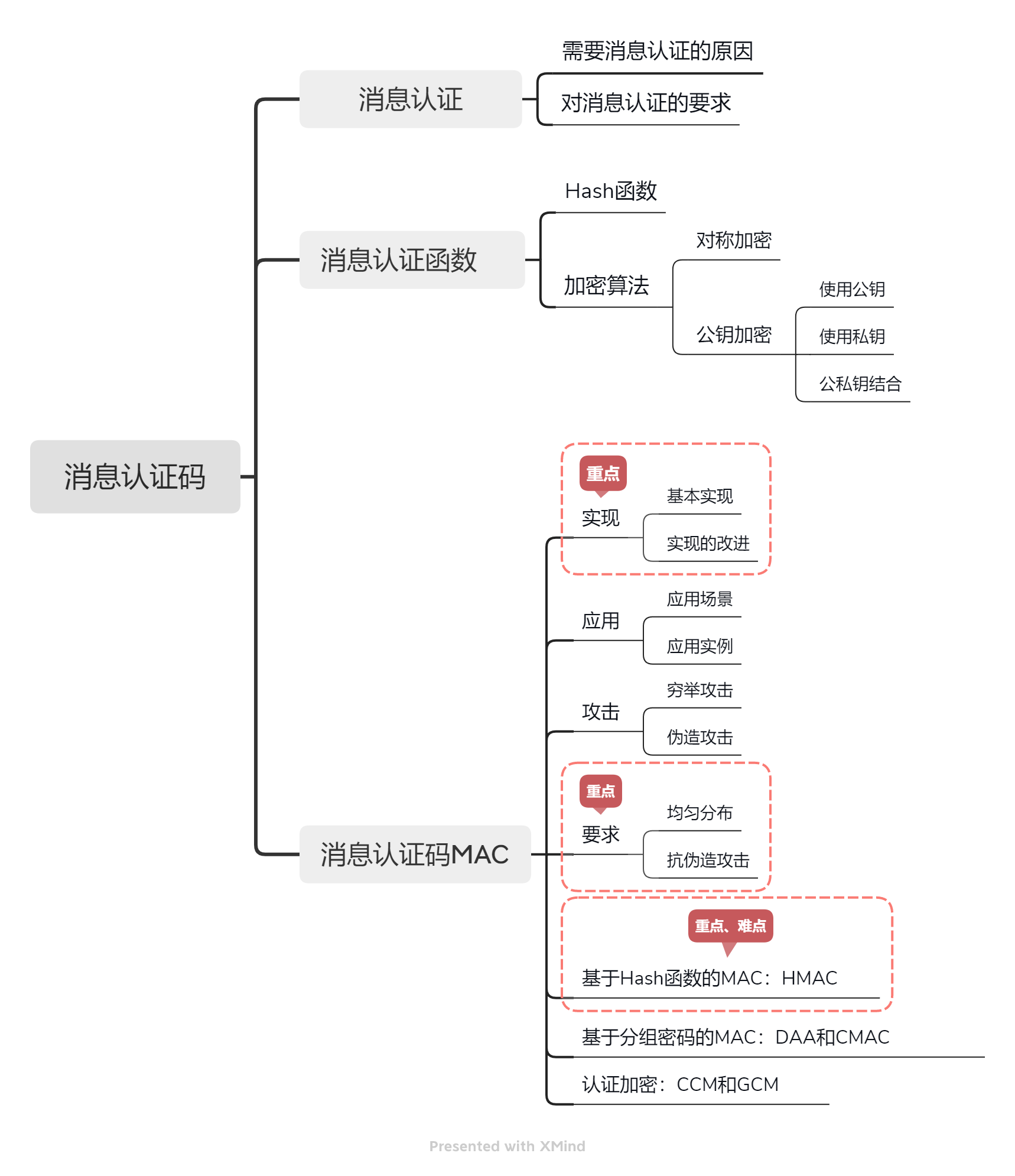
🕒 0. 思维导图
🕒 1. 常见攻击

- 【问题】Alice 给 Bob 发送的消息,其内容 或 通信特征被非法第三方 Darth获取得到
- 【解决】加密,保证消息的保密性
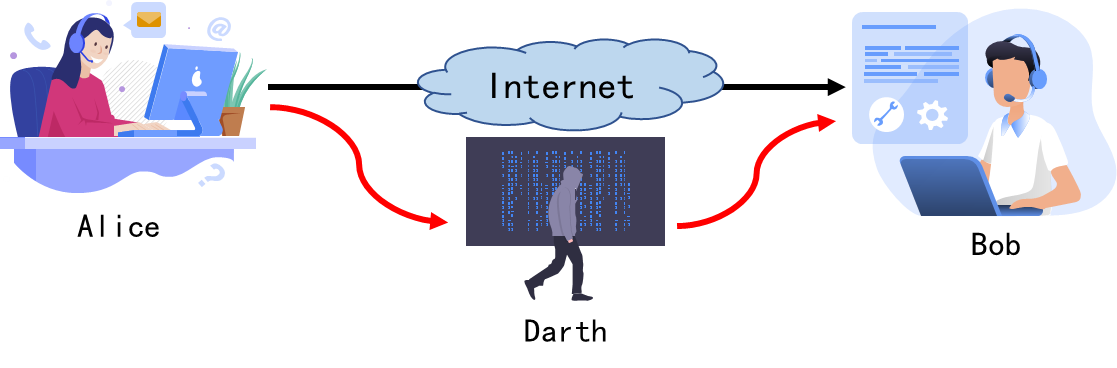
- 【问题】Alice 给 Bob 发送的消息,其内容 或 顺序 被非法第三方 Darth修改
- 【解决】消息认证,保证消息的完整性
- 【问题】Alice 给 Bob 发送的消息,Alice否认自己发过消息/Bob否认自己受到过消息
- 【解决】数字签名
🕒 2. 对消息认证的要求
- 验证收到的消息确实是来自真正的发送方(数字签名)
- 验证收到的消息是未被修改的,其顺序与及时性均正确
🕒 3. 消息认证函数
🕘 3.1 Hash
- Hash函数 将任意长的消息 映射为 固定长度的Hash值,以该值作为消息的认证符
🕘 3.2 加密
- 对整个消息加密,产生的密文作为消息的认证符
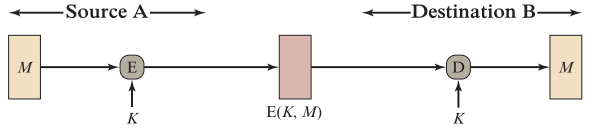
🕤 3.2.1 对称加密
-
【确认消息是保密的】
如果其他人不知道K,那么可以提供保密性,因为任何人不能恢复出明文消息M -
【确认消息的发送方】
B 能确认消息是由A 产生的,因为除B 外只有A 拥有K,才能产生出用K 解密成功的密文 -
【确认消息的完整性】
B 能确认消息是未被改变的,因为攻击者不知道密钥K,即使修改了密文的某些位,还原出的明文也是错误的 -
对称密码 既可以提供保密性,又可以提供消息认证
-
但有一个重要前提:接收方能判定M 是合法的明文
-
例如K=1的Ceasar密码,我们可以判定明文的合法性
nbsftfbupbutboeepftfbupbutboemjuumfmbnctfbujwz
↓
\hspace{3cm}↓
↓
mareseatoatsanddoeseatoatsandlittlelambseativy
-
对密文解密后,得到的明文具有普通英语的特点
-
若攻击者产生如下所示的随机字符作为密文
zuvrsoevgqxlzwigamdvnmhpmccxiuureosfbcebtqxsxq
↓
\hspace{3cm}↓
↓
ytuqrndufpwkyvhfzlcumlgolbbwhttqdnreabdaspwrwp
-
对密文解密后,得到的明文不具有普通英语的特点
-
若M 是可读文本消息,如何判别可读性,证明M正确呢?
-
若M 是不可读的文件,又如何证明M正确?
🕞 3.2.1.1 内部错误控制
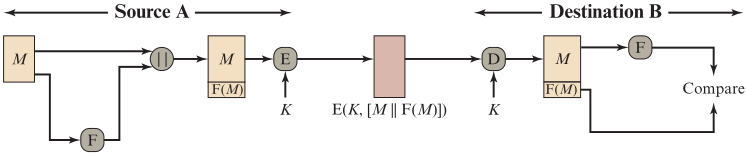
- 对明文M 进行校验,产生帧校验序列FCS(后续计网会讲)
- 将FCS 附加在明文M 后,再使用K 对整体进行加密
- 解密后,对前半部分的消息M 使用相同的校验函数F 重新计算FCS,并与收到的FCS 进行比较,相同说明 M正确
- 攻击者很难伪造这样的密文Y:
- 解密后得到的M,对其计算帧校验序列,还恰好与下方的FCS 保持一致
Q:现在密钥K是绝对保密的,若攻击者截获了传输的数据,他能看到消息M 是什么吗?那校验码FCS呢?
A:都不能
🕞 3.2.1.2 外部错误控制
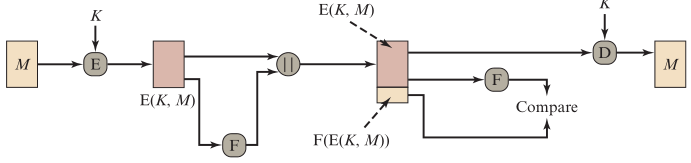
- 先使用K 对明文M 进行加密,再对密文进行校验,将FCS附加在密文后,发送给对方
Q:现在密钥K是绝对保密的,若攻击者截获了传输的数据,他能看到消息M 是什么吗?那校验码FCS呢?
A:M不能,FCS能

🕤 3.2.2 公钥加密
🕞 3.2.2.1 使用公钥PU

【确认消息是保密的】
- 发送方A 使用接收方B 的公钥PU-b 为消息M 加密
- 只有B 拥有解密的私钥PR-b,只有B 能看到消息M
Q:若攻击者截获了传输的数据,他能否伪造出一个新的密文,使得接收方解密后得到的是另外的消息M’?
A:能
【无法确认消息是真实的】
- 用来加密的公钥PU-b 是公开的
- 攻击者可以假冒成A,使用PU-b 对消息M 加密发送给B
🕞 3.2.2.2 使用私钥PR

【无法确认消息是保密的】
- 发送方A 使用自己的私钥PR-a 为消息M 加密
- 任何人都拥有解密的公钥PU-a,都能看到消息M
【确认消息是真实的】
- 若密文能用A的公钥PU-a 解密成功,说明该密文一定是用对应的私钥PR-a 加密得来,而只有A 才知道PR-a
- 若能够判别明文的合法性,那么使用该种方式 既实现了消息认证,又实现了数字签名
Q:若攻击者截获了传输的数据,他能看到消息M 是什么吗?
A:能
Q:若攻击者截获了传输的数据,他能否伪造出一个新的密文,使得接收方解密后得到的是另外的消息M’?
A:不能
🕞 3.2.2.3 公私钥结合

- 先使用发送方的私钥PR-a 为消息M 签名,实现消息认证
- 再使用接收方B的公钥PU-b 进行加密,实现消息的保密
🕘 3.3 消息认证码
🕤 3.3.1 原始版本

- 消息认证码MAC 是关于消息和密钥的函数,产生固定长度的值作为认证符
- 发送方A 使用双方共享的密钥K 对消息M 计算MAC
𝑴 𝑨 𝑪 = 𝑪 ( 𝑲 , 𝑴 ) \hspace{2cm}𝑴𝑨𝑪=𝑪(𝑲,𝑴) MAC=C(K,M) - 将MAC 附加在消息M 后一起发送给接收方B
- 相比哈希函数多了个密钥K的参与,这个密钥可以认为是身份认证的依据
Q:若攻击者截获了传输的数据,并且已知MAC的长度为n位,他能看到消息M 是什么吗?
A:能
Q:现在密钥K是绝对保密的,若攻击者将消息M 篡改为M’,他能否也同时修改MAC,使得接收方无法察觉?
A:不能
Q:现在密钥K是绝对保密的,若接收方B 对M 计算得到的MAC 与收到的完全相同,他能否确定数据 一定来自于发送方A ?
A:能,因为身份认证的依据就是密钥K
若消息认证码MAC 匹配正确,则:
(1)消息M 未被修改;
(2)消息M 来自真正的发送方;
(3)消息M 若含有序列号,则消息顺序正确
🕤 3.3.2 V2.0 版本

- 通信双方共享密钥K1、K2
- 发送方A 使用K1 对消息M 计算MAC,将其附加M 的后面
- 再使用K2 对(M+MAC)加密,发送给接收B
- 接收方B 使用K2 对密文解密,得到(M+MAC)
- 再使用K1 对消息M 计算MAC,并与接收到的MAC 比较
- 实现了消息认证与保密性
🕤 3.3.3 V2.1 版本

- 通信双方共享密钥K1、K2
- 发送方A 使用K2 对消息M 加密
- 再使用K1 对密文计算MAC,将其附加在密文后面,一起发送给接收方B
- 接收方B 使用K2 还原出明文
- 再使用K1 对密文计算MAC,将其与收到的进行比较
为什么需要消息认证码?用Hash函数/消息加密函数不够么?
🕒 4. MAC的应用
🕘 4.1 作用场景
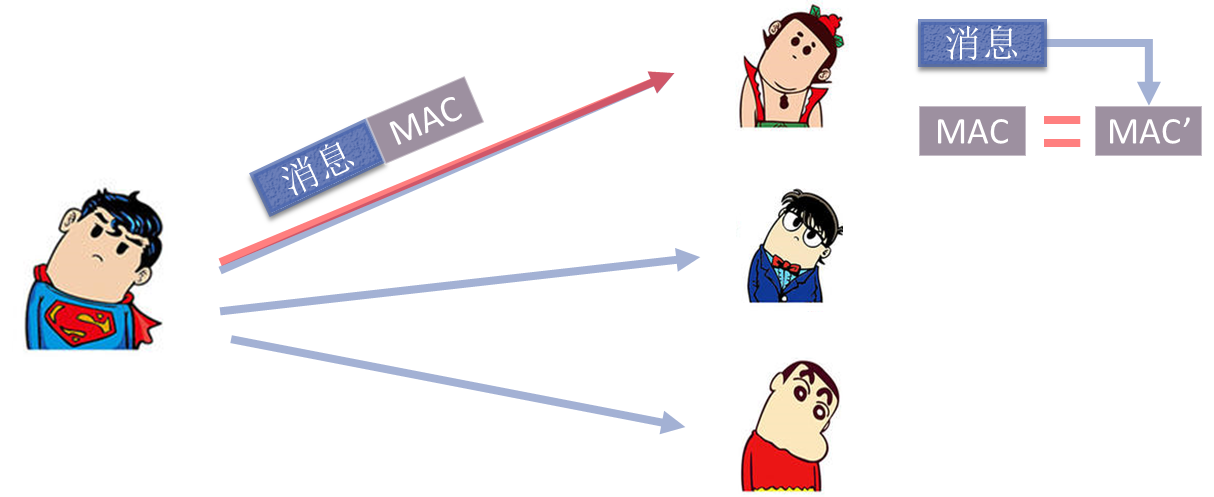
- 同一消息广播给多个接收者,消息以明文+消息认证码的形式传播,只要其中一个接收者负责验证消息的真实性

-
消息通信中,通信的某一方处理负荷很大,没有时间解密所有信息,应该做到随机选择消息验证
-
对明文形式的计算机程序进行认证,不必每次都加解密
-
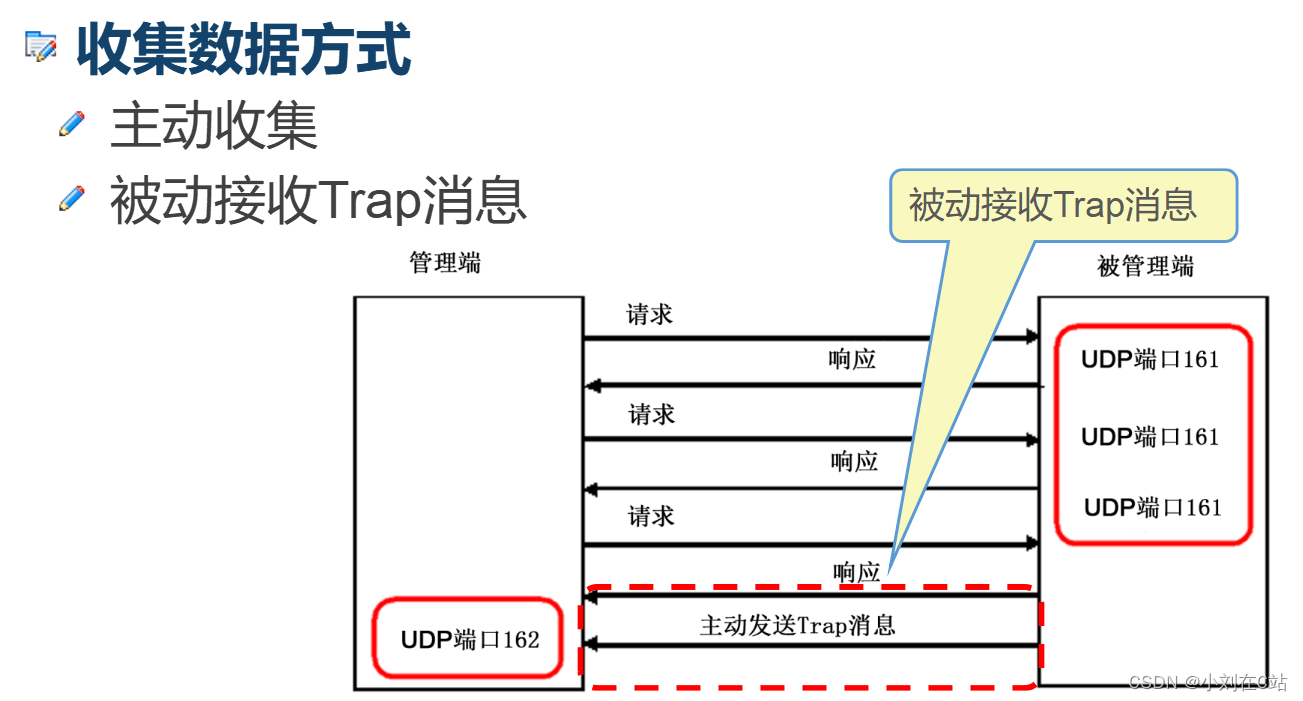
有些应用,如SNMP 不关心消息的保密性,只关心认证性
🕘 4.2 实际应用
- SWIFT:环球银行金融电信协会
- 银行与银行之间是通过SWIFT来传递交易信息的。而为了确认消息的完整性以及对消息进行验证,SWIFT中使用了消息认证码。
- TLS/SSL中使用了消息认证码。
- IPSec的子协议头认证协议AH,为IP报文提供数据完整性验证和数据源身份认证,使用的是消息认证码。
- 所有的IPSec必须实现两个算法:HMAC-MD5和HMAC-SHA1。(注:SHA1现在已不安全)
- Amazon Web Services(AWS)由亚马逊公司所创建的云计算平台
- AWS使用的主要身份验证方法就是消息认证码的一种—HMAC。
🕤 4.2.1 HMAC
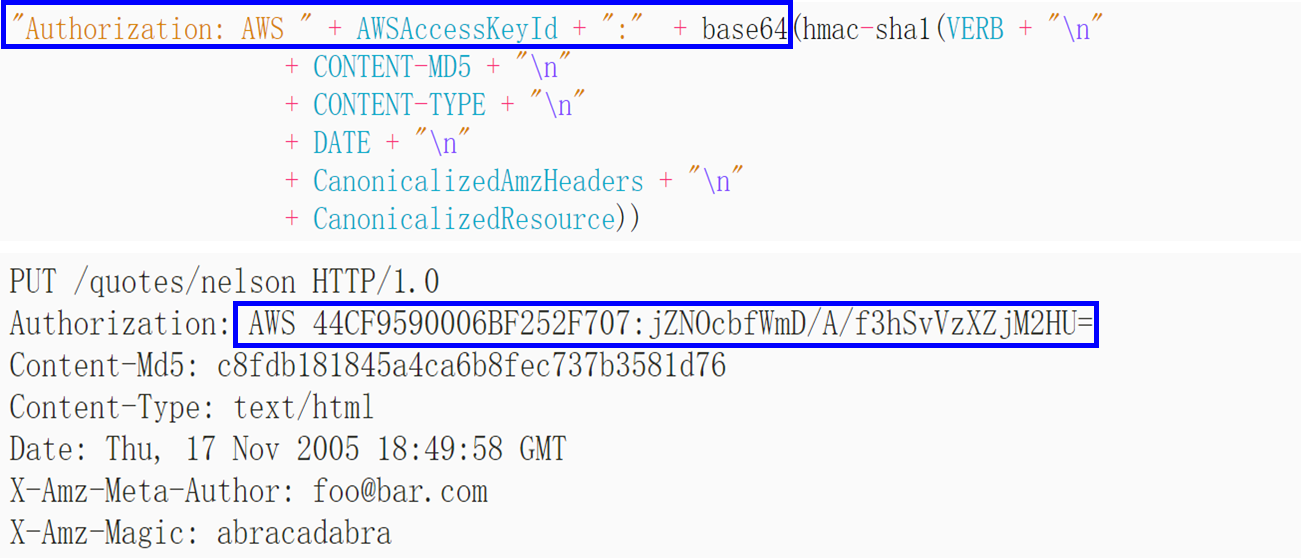
- HMAC身份验证摘要是使用提供的密钥将URI、请求时间戳和一些其他标头的组合计算得来。
- 密钥标识符和使用Base64编码的摘要一起被合并并添加到授权标头中
🕒 5. 攻击
🕘 5.1 加密
𝒀 = 𝑬 ( 𝑲 , 𝑿 ) 𝑿 = 𝑫 ( 𝑲 , 𝒀 ) 𝒀=𝑬(𝑲,𝑿) \\ 𝑿=𝑫(𝑲,𝒀) Y=E(K,X)X=D(K,Y)
- 消息加密由如上函数产生。其中𝑿 是固定长度的明文, 𝑲是收发双方共享的密钥, 𝒀是固定长度的密文
- 发送方将𝒀 发送出去,接收方通过还原𝑿 来获取消息
🕤 5.1.1 穷举攻击
𝑿
=
𝑫
(
𝑲
,
𝒀
)
𝑿=𝑫({\color{red}𝑲},𝒀)
X=D(K,Y)
2
k
\hspace{1.4cm}\color{red}2^k
2k
- 加密的安全性主要依赖于密钥 𝑲 𝑲 K
- 如给定密文 𝒀 𝒀 Y,攻击者对所有可能的密钥进行穷举攻击,直到某个 𝑲 𝒊 𝑲_𝒊 Ki,使得 𝑿 𝒊 = 𝑫 ( 𝑲 𝒊 , 𝒀 ) 𝑿_𝒊=𝑫(𝑲_𝒊,𝒀) Xi=D(Ki,Y)具有适当的明文结构
- 若密钥 𝑲 𝑲 K长度为 𝒌 𝒌 k位,穷举规模 𝟐 𝒌 𝟐^𝒌 2k次,平均尝试 𝟐 ( 𝒌 − 𝟏 ) 𝟐^{(𝒌−𝟏)} 2(k−1)次
🕘 5.2 认证
𝑴 𝑨 𝑪 = 𝑪 ( 𝑲 , 𝑴 ) 𝑴𝑨𝑪=𝑪(𝑲,𝑴) MAC=C(K,M)
- 消息认证码𝑴𝑨𝑪 由如上形式的函数产生。其中𝑴 是一个变长消息, 𝑲是收发双方共享的密钥, 𝑴𝑨𝑪是定长的认证符
- 发送方将𝑴𝑨𝑪 附于消息之后,接收方通过计算𝑴𝑨𝑪 来认证消息
🕤 5.2.1 穷举攻击
𝑴
𝑨
𝑪
=
𝑪
(
𝑲
,
𝑴
)
{\color{blue}𝑴𝑨𝑪}=𝑪({\color{green}𝑲},𝑴)
MAC=C(K,M)
2
c
2
k
\hspace{0.5cm}{\color{blue}2^c} \hspace{1.3cm} {\color{green}2^k}
2c2k
- 若密钥𝑲的位数𝒌 大于 消息认证码𝑴𝑨𝑪的位数𝒄 ,那么攻击者尝试所有可能的密钥,生成了 𝟐 𝒌 𝟐^𝒌 2k个MAC值,而MAC值一共只有 𝟐 𝒄 𝟐^𝒄 2c个
- 因此许多密钥都会产生正确的MAC值,哪个密钥才是正确的?
M
A
C
1
=
C
(
K
,
M
1
)
2
k
−
c
{\color{blue}MAC_1}=C\left(K, {\color{blue}M_{1}}\right) \hspace{0.5cm} {\color{red}2^{\boldsymbol{k - c}}}
MAC1=C(K,M1)2k−c
M
A
C
2
=
C
(
K
,
M
2
)
2
k
−
2
c
{\color{green}MAC_2}=C\left(K, {\color{green}M_{2}}\right) \hspace{0.5cm} {\color{red}2^{\boldsymbol{k}-2c}}
MAC2=C(K,M2)2k−2c
…. ….
攻击者重复如上所示的循环,直到匹配数
𝟐
𝒌
−
𝒏
𝒄
→
𝟏
𝟐^{𝒌−𝒏𝒄}→𝟏
2k−nc→1
练习题:
1、已知某MAC函数的密钥K 长度90位,MAC值为15位,现在攻击者对密钥K 发起穷举攻击,问:他在第几次循环可以得到唯一的正确密钥?
解答:
M A C 1 = C ( K , M 1 ) 2 90 − 15 {\color{blue}MAC_1}=C\left(K, {\color{blue}M_{1}}\right) \hspace{0.5cm} {\color{red}2^{\boldsymbol{90 - 15}}} MAC1=C(K,M1)290−15
M A C 2 = C ( K , M 2 ) 2 90 − 2 × 15 {\color{green}MAC_2}=C\left(K, {\color{green}M_{2}}\right) \hspace{0.5cm} {\color{red}2^{\boldsymbol{90}-2 \times 15}} MAC2=C(K,M2)290−2×15
M A C 3 = C ( K , M 3 ) 2 90 − 3 × 15 {\color{orange}MAC_3}=C\left(K, {\color{orange}M_{3}}\right) \hspace{0.5cm} {\color{red}2^{\boldsymbol{90 - 3 \times 15}}} MAC3=C(K,M3)290−3×15
. . . . . . . . . . . . \hspace{0.2cm}......\hspace{3cm}...... ............
M A C 6 = C ( K , M 6 ) 2 90 − 6 × 15 = 1 {\color{purple}MAC_6}=C\left(K, {\color{purple}M_{6}}\right) \hspace{0.5cm} {\color{red}2^{\boldsymbol{90}-6 \times 15}=1} MAC6=C(K,M6)290−6×15=1
所以需要循环 6 6 6次
2、已知某MAC函数的密钥K 长度90位,MAC值为15位,现在攻击者对密钥K 发起穷举攻击,问:他在第几次循环可以得到唯一的正确密钥?
解答: 90 ÷ 26 = 3...12 90 \div 26 =3...12 90÷26=3...12,所以需要循环 3 + 1 = 4 3+1=4 3+1=4次
🕤 5.2.2 伪造攻击
Δ
M
=
X
1
⊕
X
2
…
⊕
X
m
−
1
⊕
X
m
\Delta M=X_{1} \oplus X_{2} \quad \ldots \oplus X_{m-1} \oplus X_{m}
ΔM=X1⊕X2…⊕Xm−1⊕Xm
M
A
C
=
E
(
K
,
Δ
M
)
\qquad MAC=E(K, \Delta M)
MAC=E(K,ΔM)
Δ
M
=
Y
1
⊕
Y
2
…
⊕
Y
m
−
1
⊕
Y
m
\Delta M=Y_{1} \oplus Y_{2} \quad \ldots \oplus Y_{m-1} \oplus Y_{m}
ΔM=Y1⊕Y2…⊕Ym−1⊕Ym
Y
m
=
Y
1
⊕
Y
2
…
⊕
Y
m
−
1
⊕
Δ
M
Y_{m}=Y_{1} \oplus Y_{2} \quad \ldots \oplus Y_{m-1} \oplus \Delta M
Ym=Y1⊕Y2…⊕Ym−1⊕ΔM
- 攻击者可在消息前自由增加内容,接收方无法察觉
🕒 6. 对消息认证码的要求
🕘 6.1 抗伪造攻击
𝑴 𝑨 𝑪 ( 𝑲 , 𝑴 ) ≠ 𝑴 𝑨 𝑪 ( 𝑲 , 𝑴 ′ ) 𝑴𝑨𝑪(𝑲,𝑴){\color{red}≠}𝑴𝑨𝑪(𝑲,{\color{red}𝑴^′} ) MAC(K,M)=MAC(K,M′)
- 若攻击者已知 M M M,已知MAC,不知道 K K K
- 他无法伪造出消息 M ’ M’ M’,使得 M ’ M’ M’的MAC值与给定的相同,在计算上是不可行的
🕘 6.2 均匀分布
𝑷 𝒓 ( 𝑴 𝑨 𝑪 ( 𝑲 , 𝑴 ) = 𝑴 𝑨 𝑪 ( 𝑲 , 𝑴 ’ ) = 𝟐 − 𝒄 𝑷𝒓(𝑴𝑨𝑪(𝑲,𝑴)=𝑴𝑨𝑪(𝑲,𝑴^’ ) ={\color{red}𝟐^{−𝒄}} Pr(MAC(K,M)=MAC(K,M’)=2−c
- M A C ( K , M ) MAC(K,M) MAC(K,M)应是均匀分布的
- 对任何随机选择的消息 M M M和 M ’ M’ M’, M A C ( K , M ) = M A C ( K , M ’ ) MAC(K,M)= MAC(K,M’) MAC(K,M)=MAC(K,M’)的概率为为 𝟐 − 𝒄 𝟐^{−𝒄} 2−c, c c c为MAC的位数
- MAC已知 M ’ M’ M’是 M M M的某个已知的变换,即 M ’ = f ( M ) M’=f(M) M’=f(M)
- 我们也要求, M A C ( K , M ) = M A C ( K , M ’ ) MAC(K,M)= MAC(K,M’) MAC(K,M)=MAC(K,M’)的概率为为 𝟐 − 𝒄 𝟐^{−𝒄} 2−c, c c c为MAC的位数
🕒 7. 基于Hash函数的MAC——HMAC
🕘 7.1 应用
- HMAC在各种网络应用中都能找到,如安全传输层协议TLS、网络安全IPSec。并且,HMAC还是美国国家标准与技术研究院NIST所使用的标准。
- HMAC得到广泛应用的原因主要是执行速度相对较快、有许多共享的代码库可以进行实现。
🕘 7.2 设计目标
- 对密钥的使用和处理简单
- 直接使用现有Hash函数
- 进行Hash函数的替代很容易
- 保持Hash函数原有的性能
- 已知Hash的强度, MAC强度就可确定
🕘 7.3 流程
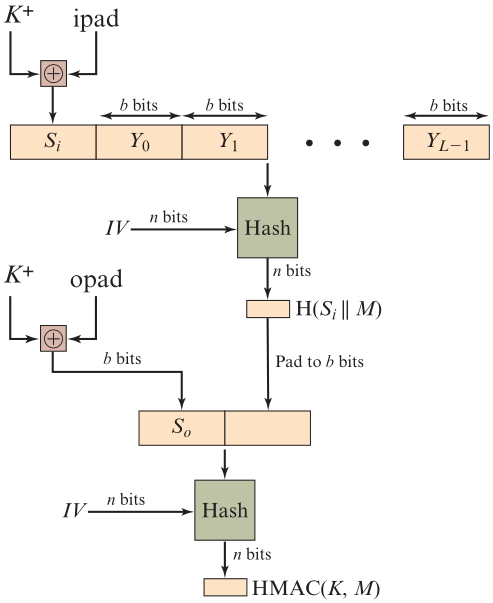
- 在密钥 K K K 左边填充0,得到 b b b位的 K + K^+ K+
- 构造 i p a d = 00110110 ipad = 00110110 ipad=00110110 重复 b / 8 b/8 b/8次,使其和 K + K+ K+等长
- 将 K + K^+ K+ 与 i p a d ipad ipad 进行按位异或,产生分组 S i S_i Si
- 将填充内容 P P P、长度块 L L L附加在消息之后,变为分组长度 b b b 的整数倍
- 将填充后的消息 M M M 附加在 S i S_i Si之后
- 将 ( S i + M ) (S_i+M) (Si+M)、初始值 I V IV IV 一起输入到选定的Hash函数中,产生Hash值 H ( S i + M ) H(Si+M) H(Si+M)
- 构造 o p a d = 01011100 opad = 01011100 opad=01011100 重复 b / 8 b/8 b/8次
- 将 K + K+ K+ 与 o p a d opad opad 进行按位异或,产生分组 S o S_o So
- 将前面得到的Hash值 填充至 b b b位,附加在 S o S_o So 后面
- 将 ( S o + H ) (S_o+H) (So+H)、初始值 I V IV IV 一起输入到选定的Hash函数中,产生的Hash值 即 消息认证码HMAC
练习题:
现在Hash函数是将所有分组进行按位异或,且分组长度b=8,填充内容P为10…00,消息长度区域共2位。
若密钥K=110,请给出消息001的HMAC。
解答: K + = 00000110 K^+ =00000110 K+=00000110
i p a d = 00110110 o p a d = 01011100 ipad = 00110110 \qquad opad = 01011100 ipad=00110110opad=01011100
S i = K + ⊕ i p a d = 00110000 S_i = K^+\oplus ipad = 00110000 Si=K+⊕ipad=00110000
Y = 001 100 11 Y = 001 \ 100 \ 11 Y=001 100 11(明文分组)
H 1 = H ( S i ∣ ∣ Y ) = S i ⊕ Y = 00000011 H_1=H(S_i \mid\mid Y) = S_i \oplus Y = 00000011 H1=H(Si∣∣Y)=Si⊕Y=00000011
S 0 = K + ⊕ o p a d = 01011010 S_0 = K^+\oplus opad = 01011010 S0=K+⊕opad=01011010
H 2 = H ( S 0 ∣ ∣ H 1 ) = S 0 ⊕ H 1 = 01011001 H_2=H(S_0 \mid\mid H_1) = S_0 \oplus H_1 = 01011001 H2=H(S0∣∣H1)=S0⊕H1=01011001
🕘 7.4 执行时间

- HAMC多执行了三次Hash函数: S i S _i Si, S 0 S _0 S0和内部Hash产生的分组
- 对长消息来说,HMAC和Hash函数的执行时间大致相同
🕘 7.5 设计目标
- 对密钥的使用和处理简单
- 直接使用现有Hash函数
- 进行Hash函数的替代很容易
- 保持Hash函数原有的性能
- 已知Hash的强度,MAC强度就可确定
🕒 8. 基于分组密码的MAC
🕘 8.1 DAA
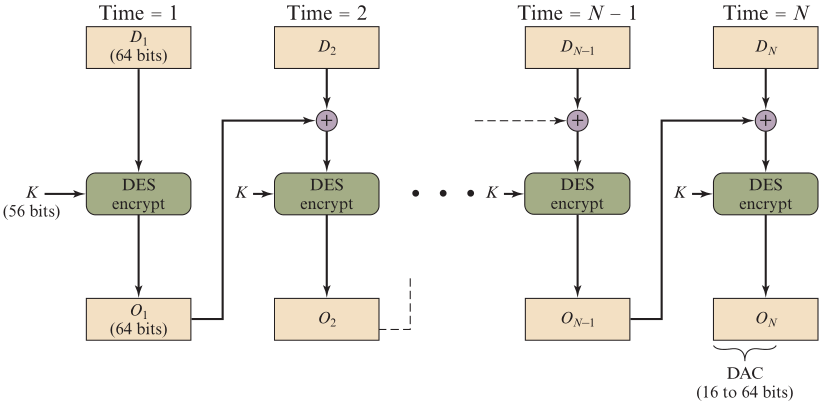
- 数据认证算法DAA 使用广泛,它建立在DES之上,采用CBC密文分组链接模式
- 因为安全弱点和算法陈旧,容易产生伪造攻击,目前已经废止了
- 将要认证的数据 划分成 一个个64位分组,最后一个不足64位就在后面填充0
- 第一个分组D1 与 密钥K 一起输入到DES加密算法中,产生第一个输出O1
- 第二个分组D2 与 上一个输出O1 异或的结果,与密钥K 一起输入到DES加密算法中,产生第二个输出O2
- 最后的分组Dn 与 上一个输出On-1 异或的结果,与密钥K 一起输入到DES加密算法中,产生认证码DAC
- 容易产生伪造攻击,因此需要严格限制消息长度,如64位
🕘 8.2 CMAC
- CMAC建立在AES之上,采用CBC密文分组链接模式,是DAA的进阶版
🕤 8.2.1 消息长度是分组长度的整数倍
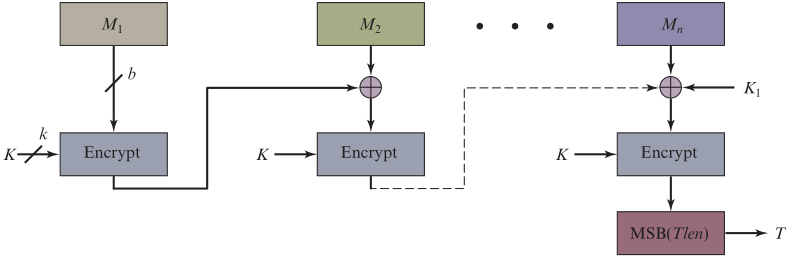
- 将 b位的第一个分组M1 与 k位的密钥K 输入到加密算法中,产生第一个输出C1
- 将 b位的第二个分组M2 与 C1 进行异或,产生的结果与k位的密钥K 输入到加密算法中,产生第二个输出C2
- 将 b位的最后分组Mn 分别与 Cn-1 和密钥K1 进行异或,再与 k位的密钥K 输入到加密算法中,产生的Cn 高t位即认证码
🕤 8.2.2 消息长度不是分组长度的整数倍
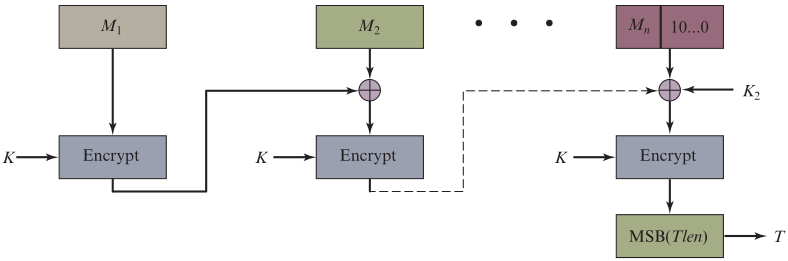
- 将最后一个分组后面填充10000…000,凑成b位
- 将 b位的第一个分组M1 与 k位的密钥K 输入到加密算法中,产生第一个输出C1
- 将 b位的第二个分组M2 与 C1 进行异或,产生的结果与k位的密钥K 输入到加密算法中,产生第二个输出C2
- 将 b位的最后分组Mn 分别与 Cn-1 和密钥K2 进行异或,再与 k位的密钥K 输入到加密算法中,产生的Cn 高t位即认证码
🕒 9. 认证加密——CCM
- 认证加密(AE)是指在通信中同时提供保密性和认证的加密系统。
- 许多应用和协议都需要这两种安全保证
- 以前,两类安全系统都是分离设计,近几年,才对两者进行了合并
方 案 协 议 H->E / A->E SSL/TLS E->A IPSec E+A SSH/WEP \begin{array}{|c|c|} \hline 方案 & 协议 \\ \hline \text{H->E} & \text{/} \\ \hline \text{A->E}& \text{SSL/TLS} \\ \hline \text{E->A} & \text{IPSec} \\ \hline \text{E+A} & \text{SSH/WEP} \\ \hline \end{array} 方案H->EA->EE->AE+A协议/SSL/TLSIPSecSSH/WEP
-
先Hash再加密: h = H ( M ) , E ( K , ( M ∣ ∣ h ) ) h=H(M),E(K,(M||h)) h=H(M),E(K,(M∣∣h))
-
先认证再加密: T = M A C ( K 1 ) , E ( K 2 , M ∣ ∣ T ) T=MAC(K1),E(K2,M||T) T=MAC(K1),E(K2,M∣∣T)
-
先加密再认证: C = E ( K 2 , M ) , T = M A C ( K 1 , C ) C=E(K2,M),T=MAC(K1,C) C=E(K2,M),T=MAC(K1,C)
-
独立进行加密和认证: C = E ( K 2 , M ) , T = M A C ( K 1 , M ) , ( C , T ) C=E(K2,M), T=MAC(K1,M), (C, T) C=E(K2,M),T=MAC(K1,M),(C,T)
-
CCM:分组密码链-消息认证码
-
CCM由NIST提出的用于保护IEEE 802.11WIFI无线局域网安全的标准
-
CCM执行的是独立进行加密和认证(E+A)的方案
🕘 9.1 认证
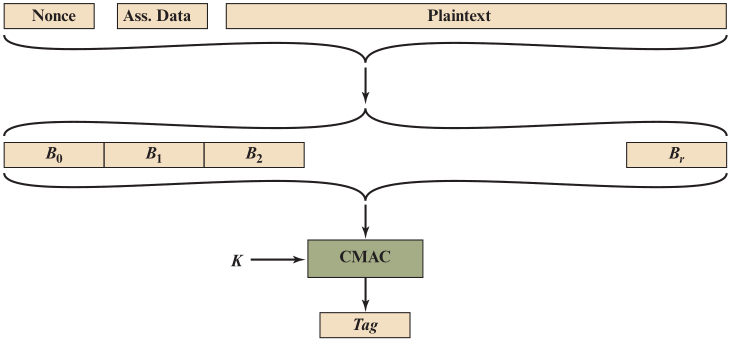
- 输入由三部分构成:临时量 N N N、相关数据 A A A明文 P P P
- 临时量 N N N,作为负载和相关数据的补充
- 对每条消息 N N N取值唯一,以防止重放攻击等。
- 将要被认证,但是不需要加密的相关数据 A A A,如协议头等。
- 用户需要发送的明文 P P P
- 使用格式函数将 ( N , A , P ) (N,A,P) (N,A,P)格式化为分组 𝑩 𝟎 、 𝑩 𝟏 … 𝑩 𝒓 𝑩_𝟎 、𝑩_𝟏…𝑩_𝒓 B0、B1…Br
- 将 密钥 K K K 和 分组 𝑩 𝟎 、 𝑩 𝟏 … 𝑩 𝒓 𝑩_𝟎 、𝑩_𝟏…𝑩_𝒓 B0、B1…Br输入到CMAC中进行处理,生成 T l e n Tlen Tlen位的MAC
🕘 9.2 加密

- 把明文P、各个计数器值 𝑪 𝒕 𝒓 𝟏 、 𝑪 𝒕 𝒓 𝟐 … 𝑪 𝒕 𝒓 𝒎 𝑪_{𝒕𝒓𝟏} 、𝑪_{𝒕𝒓𝟐}… 𝑪_{𝒕𝒓𝒎} Ctr1、Ctr2…Ctrm和密钥K做为输入,AES作为加密算法、计数器模式为工作模式进行加密,得到密文C
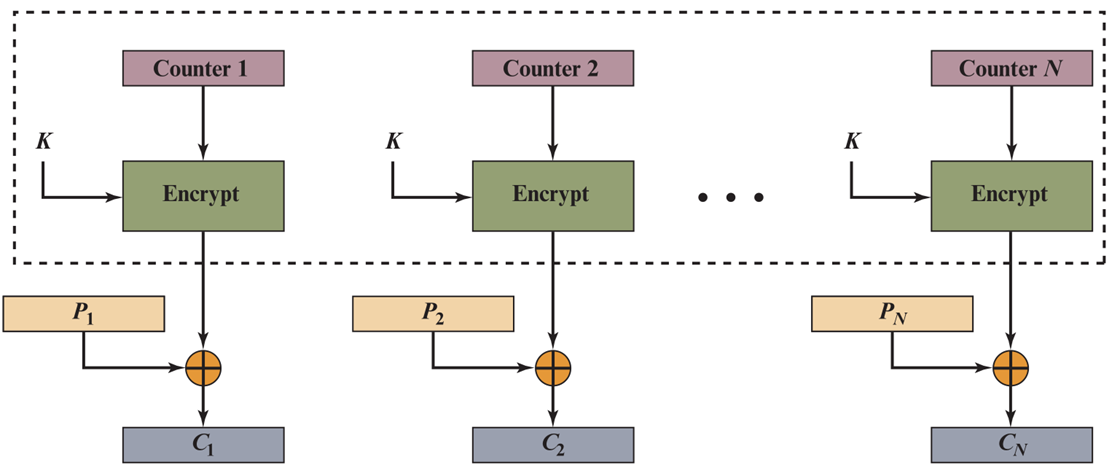
- 使用计数器模式进行加密,收发双方要提前确定计数器的初始值 𝑪 𝒕 𝒓 𝟎 , 𝑪 𝒕 𝒓 𝟏 、 𝑪 𝒕 𝒓 𝟐 … 𝑪 𝒕 𝒓 𝒎 𝑪_{𝒕𝒓𝟎}, 𝑪_{𝒕𝒓𝟏} 、𝑪_{𝒕𝒓𝟐}… 𝑪_{𝒕𝒓𝒎} Ctr0,Ctr1、Ctr2…Ctrm由 𝑪 𝒕 𝒓 𝟎 𝑪_{𝒕𝒓𝟎} Ctr0进行变换得到。
- 把计数器初始值值 𝑪 𝒕 𝒓 𝟎 𝑪_{𝒕𝒓𝟎} Ctr0和密钥 K K K做为输入,AES作为加密算法进行加密,对加密的结果取最左边的 T l e n Tlen Tlen位
- 再与认证得到MAC值进行异或,异或后的结果链接到加密产生的密文 C C C后面
OK,以上就是本期知识点“消息认证码”的知识啦~~ ,感谢友友们的阅读。后续还会继续更新,欢迎持续关注哟📌~
💫如果有错误❌,欢迎批评指正呀👀~让我们一起相互进步🚀
🎉如果觉得收获满满,可以点点赞👍支持一下哟~








![[搞点好玩的] JETSONNANO 受苦记 -- 001 (布置环境,未完待续)](https://img-blog.csdnimg.cn/747b2a70c9db481e91fa7d01e1cf7b37.png)