第十九课 卷积层的填充和步幅

目录

理论部分

实践部分

---

理论部分

首先看一下卷积层的填充。

上图所示的情况会有个问题，如果卷积核不变的话（一直是5*5的卷积核），那么我的网络最多也就只能弄到第七层了，如果我想搭建更深的网络的话是不被允许的。

那么填充就是可以解决这个问题。

填充的基本思想是在输入的四周添加0元素，以达到输出比之前更大的目的。

填充的行数和列数的选取是有讲究的，如下图所示，填充完毕后它的输出与填充之前的输出的形状是一样的，区别就是网络的层数会因为输入的填充而变多，卷积效果更好。

下面看一下步幅。

如果输入比较大的话，而且我卷积核很小的话，我需要经过很多层才会得到一个较小的输出。这个很痛苦，因为层数越多计算越复杂！

那么这里的步幅就是解决这个问题的，他可以使输出的大小和层数是指数相关的。

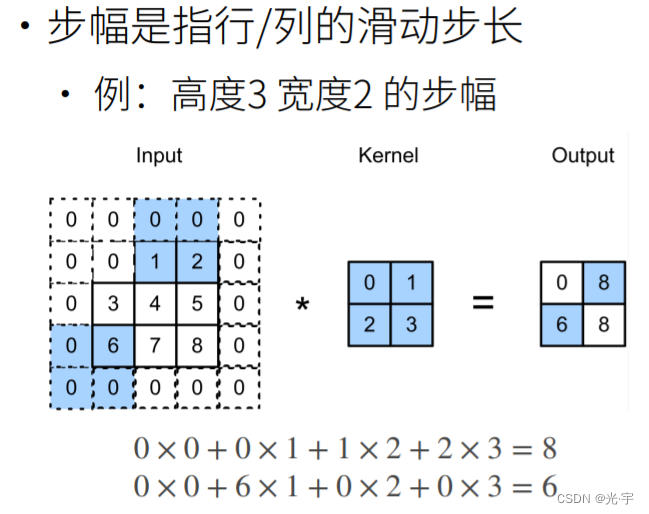
如上图所示，正常来讲的话，当卷积核做好一次卷积运算的话会往右移一个，但是设置了步幅之后，它会往右移两个或往右移多个。

注意这里的步幅还可以设置高度，也就是说每行算完卷积后，我往下移几个。

实践部分

代码：

#填充和步幅
#在所有侧边填充1个像素
import torch
from torch import nn
def comp_conv2d(conv2d, X):
    X = X.reshape((1, 1) + X.shape)#给输入矩阵添加输入和输出通道数这两个信息
    Y = conv2d(X)
    return Y.reshape(Y.shape[2:])
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)#上下左右各填充一行
X = torch.rand(size=(8, 8))
print(comp_conv2d(conv2d, X).shape)#n-k+p+1=8-3+2+1=8
#填充不同的高度和宽度
conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))#左右添加1列，上下添加2行
print(comp_conv2d(conv2d, X).shape)#输出的行：8-5+4+1；输出的列：8-5+2+1
#将高度和宽度的步幅设置为2
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)#stride表示步幅设为2，这是p=k-1的情况
print(comp_conv2d(conv2d, X).shape)#所以(n+step-1)/s=(8+2-1)/2=4.5向下取整=4
torch.Size([4, 4])
#一个稍微复杂的例子
conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))#这里p不等于k-1
print(comp_conv2d(conv2d, X).shape)#所以【（n-k+p+s）/s】=[(8-3+0+3)/3]=向下取整=2
                                   #同样列数为【（8-5+1+4）/4】=2