【物理应用】大气辐射和透射率模型及太阳和月亮模型（Matlab代码实现）

news2024/9/21 2:49:52

💖💥💥💞💞欢迎来到本博客❤️❤️💥💥🥇
🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。
📝个人主页：研学社的博客
🥇 官方认证：Matlab领域优质创作者
🎉点赞➕评论➕收藏 == 养成习惯（一键三连）😋

⚡希望大家多多支持🤗~一起加油 😁

⛳️座右铭：行百里者，半于九十。

目录

📋1 概述

📝2 运行结果

📃3 参考文献

📋4 Matlab代码及文章阅读

📋1 概述

LOWTRAN7 是空军研究实验室（AFRL）于 1988 年 8 月发布的大气辐射和透射率模型。该项目是将 LOWTRAN7 太阳和月亮模型翻译成 matlab。应该注意的是，LOWTRAN7已被MODTRAN和SAMM取代。对于高质量的太阳和月亮图像，应改用AFRL的CBSD模型。LOWTRAN 7 是一种低分辨率传播模型和计算机代码，用于预测 0 至 50，000 cm- 1 的大气透射率以及天空热辐射和散射辐射，分辨率为 20 cm-1。

在 LOWTRAN7 中，可以计算来自太阳或月亮的直射光或散射光。太阳的辐照度是从光谱中插值的，并应用轨道校正来补偿地球的轨道离心率。月球的辐照度是使用Robert E. Turner等人开发和发表的数学模型计算的。（1975）光学厚大气中的自然和人工照明，密歇根环境研究所，AD-A021 998，合同号。DAAA21-74-C-0331.（本文包括月球模型将光谱几何反照率（1988年所知）、相位因子和月球的角度范围应用于轨道校正的太阳光谱。结果显示在项目图像中。

📝2 运行结果

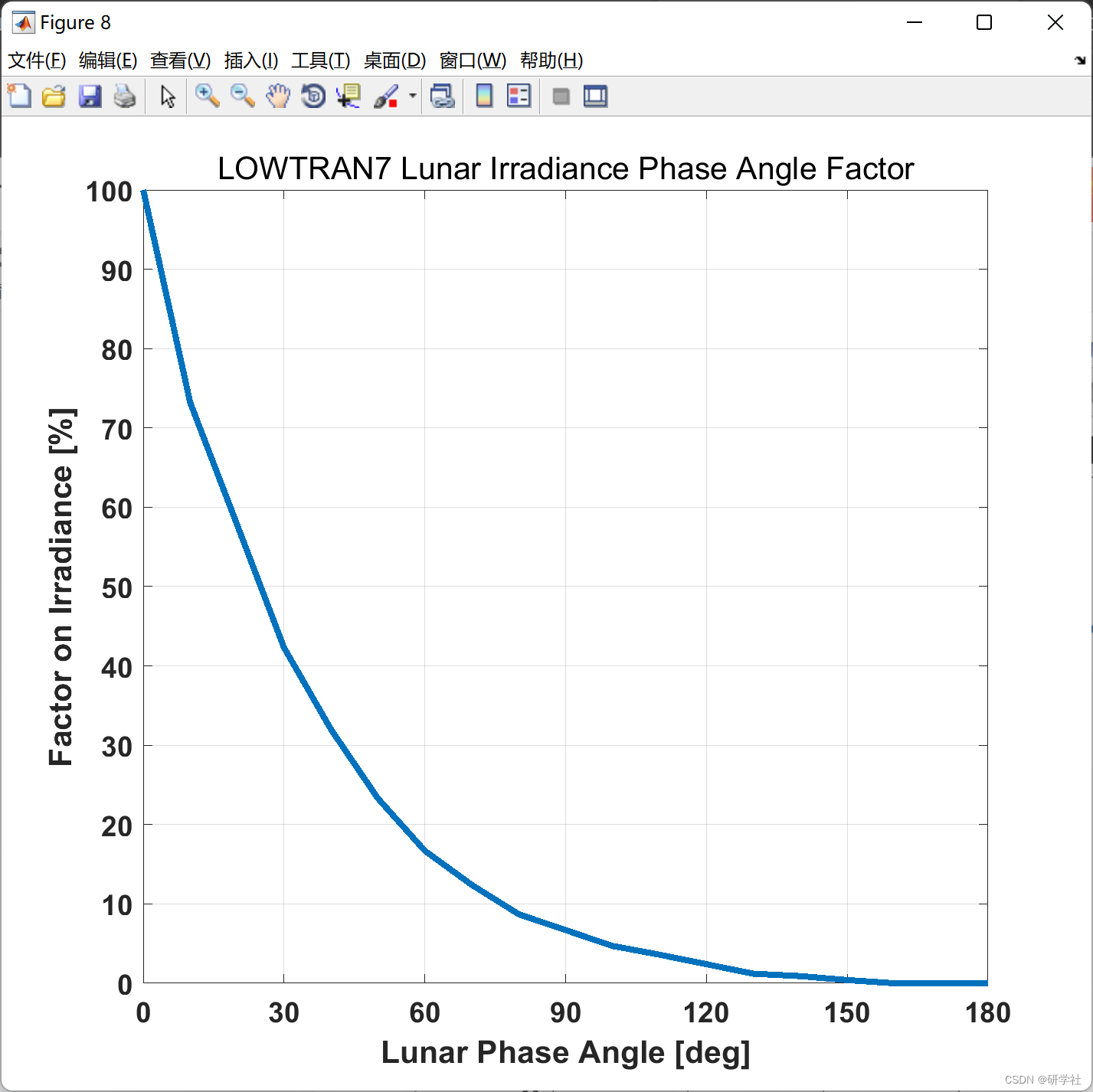
部分代码：

%% *solar spectrum*
Lambda = 0.175:0.0001:5.0; % (micron)
V = 10000./Lambda; % (cm^-1)
sun = zeros(size(V));
for i = 1:numel(V)
[sun(i)] = SUN(V(i));
end
figure('Color','White','Units','Pixels','Position',[1 300 900 600]);
plot(Lambda,sun,'linewidth',2);
xlabel('Wavelength (\lambda) [\mum]');
ylabel('Solar Irradiance [W m^{-2} \mum^{-1}]');
title('LOWTRAN7 Exoatmosphere Solar Spectrum','fontsize',16);
set(gca,'fontsize',14,'fontweight','bold');

%% *position for time/day*
IDAY = 1:365;
THETAS = zeros(size(IDAY));
PHIS = zeros(size(IDAY));
figure('color','white','units','pixels','position',[60 200 1000 800]);
subplot(2,1,1);
for TIME = [0 6 12.25 18]
for i = 1:length(IDAY)
[THETAS(i),PHIS(i)] = SUBSOL(TIME,IDAY(i));
end
plot(IDAY,PHIS,'linewidth',3,'DisplayName',['UTC=' num2str(TIME) 'h']);
hold on;
end
xlabel('Day of Year'); ylabel('\phi (deg)');
leg = legend('location','southeast');
set(gca,'fontsize',14,'fontweight','bold');
xlim([0 365]); ylim([0 360]); set(gca,'ytick',[0 90 180 270 360]);
title({'LOWTRAN7 Subsolar Latitude (\theta) and Longtitude (\phi)'});
subplot(2,1,2);
plot(IDAY,THETAS,'k','linewidth',3);
xlabel('Day of Year'); ylabel('\theta (Declination) (deg)');
set(gca,'fontsize',14,'fontweight','bold');
xlim([0 365]); ylim([-31 31]); set(gca,'ytick',[-31 -23.5 -15 -7.5 0 7.5 15 23.5 31]);
hold on;
% add Earth's Obliquity
plot([0 365],[23.5 23.5],'--b');
plot([0 365],[-23.5 -23.5],'--b');
plot([0 365],[0 0],'--b');
% add equinox and solstice dates
plot([81 81],[-30 30],'--b');
plot([172 172],[-30 30],'--b');
plot([267 267],[-30 30],'--b');
plot([354 354],[-30 30],'--b');

%% *source zenith angle at points along a line-of-sight*
j = 1;
figure('color','white','units','pixels','position',[200 150 1000 800]);
for PSIO = 0:60:180 % (deg) azimuth subtended between LOS and line to Sun
subplot(2,2,j);
IARBO = 0; % not a special case
for DELO = 5:5:45 % (deg) Sun's zernith
BETA = 1:34; % (deg) Earth center angle along the LOS
xDEL = zeros(size(BETA));
for i = 1:numel(BETA)
[xDEL(i)] = DEL(PSIO,DELO,BETA(i),IARBO);
end
plot(BETA,xDEL, ...
'DisplayName',['Solar Z_0 = ' num2str(DELO) '\circ']);
hold on;
ylim([0 90]); xlim([0 35]);
xlabel('\beta [deg]'); ylabel('Solar Zenith at this \beta [deg]');
title(['\Delta \phi LOS \rightarrow Sun = ' num2str(PSIO) '\circ']);
set(gca,'fontsize',14,'fontweight','bold');
end
if (j == 4)
k = legend('location','southeast');
k.FontSize = 9;
end
j = j + 1;
end

%% *source zenith angle at points along a line-of-sight*
j = 1;
figure('color','white','units','pixels','position',[200 150 1000 800]);
for PSIO = 0:60:180 % (deg) azimuth subtended between LOS and line to Sun
subplot(2,2,j);
IARBO = 0; % not a special case
for DELO = 5:5:45 % (deg) Sun's zernith
BETA = 1:34; % (deg) Earth center angle along the LOS
xPSI = zeros(size(BETA));
for i = 1:numel(BETA)
[xPSI(i),~] = PSI(PSIO,DELO,BETA(i),IARBO);
end
plot(BETA,xPSI, ...
'DisplayName',['Solar Z_0 = ' num2str(DELO) '\circ']);
hold on;
xlim([0 35]); ylim([0 180]); set(gca,'ytick',[0 30 60 90 120 150 180]);
xlabel('\beta [deg]'); ylabel('Solar Zenith at this \beta [deg]');
title(['\Delta \phi LOS \rightarrow Sun = ' num2str(PSIO) '\circ']);
set(gca,'fontsize',14,'fontweight','bold');
end
if (j == 4)
k = legend('location','southeast');
k.FontSize = 9;
end
j = j + 1;
end

%% *solar scattering*
% for the inputs chosen, the plots look the same as the zenith at path pt
% above
IARB = 0;
j = 1;
figure('color','white','units','pixels','position',[200 150 1000 800]);
for PSI = 0:60:180 % (deg) azimuth subtended between LOS and line to Sun
subplot(2,2,j);
IARBO = 0; % not a special case
for SOURCEZEN = 5:5:45 % (deg) Source zernith

PTHZEN = 0:90; % (deg) Path Zenisty
xSCTANG = zeros(size(PTHZEN));
for i = 1:numel(PTHZEN)
[xSCTANG(i)] = SCTANG(SOURCEZEN,PTHZEN(i),PSI,IARB);
end
plot(PTHZEN,xSCTANG, ...
'DisplayName',['Solar Z_0 = ' num2str(SOURCEZEN) '\circ']);
hold on;
ylim([0 90]); xlim([0 35]);
xlabel('Path Zenith [deg]'); ylabel('Scattering Angle [deg]');
title(['\Delta \phi LOS \rightarrow Sun = ' num2str(PSI) '\circ']);
set(gca,'fontsize',14,'fontweight','bold');
end