大家第一次接触 HTTPS 协议的时候是不是和我一样,非常困惑。
这玩意概念又多又繁琐。尤其是里面的公钥私钥啥的。
当时就特别想知道,为什么用公钥加密却不能用公钥解密?
看完这篇文章你会弄明白,同时还会解锁很多HTTPS里的细节知识点。
今天,我们就先从对称加密和非对称加密聊起吧。
对称加密和非对称加密
小学上课的时候,都传过小纸条吧?传纸条的时候每个拿到纸条的同学都会忍不住看一眼,毫无隐私可言。
假设班花想对我表白,又不想在传的过程中让别人发现她的情意绵绵。
就会在课间十分钟里告诉我,"每个字母向左移动一位,就是我想对你说的话"。
然后在上课的时候,递出纸条,上面写了 eb tib cj。每个帮助传递纸条的同学看了之后,都暗骂“谜语人,你给我滚出哥谭镇”。
嘿嘿,你们不懂,我懂。
我拿到纸条后,将每个字母向左移动一位,得到 da sha bi。
什么话,这是什么话。
坏女人想要毁我向道之心?我果断拒绝了她的表白。

现在回忆起来,感动之余,会发现,像这种,将一段大家看得懂的信息(明文)转换为另一段大家看不懂的信息(密文),其实就是加密。
像这种“左移”的加密方法,其实就是所谓的秘钥。而这种加密和解密用的都是同一个秘钥的加密形式,就叫对称加密。

对称加密
那既然有对称加密,那就有非对称加密。
不同点在于,非对称加密,加密和解密用到的不是同一个秘钥,而是两个不一样的秘钥,分别是公钥和私钥。

非对称加密
公钥负责加密,私钥负责解密。公钥人人可得,私钥永远不泄露。
那么问题就来了。
为什么用公钥加密,却不能用公钥解密?
这其实就涉及到公钥和私钥加密的数学原理了。
说白了加密就是将一个已知的数字根据一定的规则转换变成另一个数字,以前这些数字放在一起都可读,但是经过这么一转换,就变得不可读了。
也就是说加密的本质就是 num -> x (num是已知数,x是未知数)。
比如班花操作的加一减一就是很简单的转换方式。
那我们换个复杂的,比如求余运算。
假设现在有个求余运算公式。
5^2 mod 7 = 25 mod 7 = x这个公式就很简单。在已知5的2次方和7的情况下,很容易得到x=4。
但是如果我们换一下x的位置。
5^x mod 7 = 4求x等于多少的时候,上面的等式能成立呢?
那就麻烦多了。
5^0 mod 7 = 1
5^1 mod 7 = 5
5^2 mod 7 = 4
5^3 mod 7 = 6
5^4 mod 7 = 2虽然麻烦了一些,但还是能反推得到x=2时等式成立。
但如果上面的模数字变得巨大无比呢?
5^x mod 56374677648 = 4那这时候计算机只能挨个去试才能算出。正常CPU要跑好多年才能算出来,所以可以认为算不出来。
其实上面的公式就是将 5 加密成了4。如果已知x,就很容易算出等式右边的结果是4,而反过来,从4却难以反推得到出x的值是多少。因此说这样的取模算法是不可逆的。
虽然取模运算是不可逆的,但是结合欧拉定理,却可以让这个公式在一定条件下变得有点“可逆”(注意是加了引号的)。
我们来看下是怎么做的。
我们将x掰成两瓣,变成p和q的乘积。
原文^(p*q) mod N = 原文如果p, q, N选取得当,原文一波取模操作之后还是变回原文。
知道这个没用,但是结合欧拉定理,再经过一些我们都看不懂的推导过程,就可以将上面的公式变换成下面这样。
原文^(p) mod N = 密文
密文^(q) mod N = 原文结合欧拉公式的计算过程大家感兴趣可以查查。但这里只知道结论就够了。
也就是说,知道 p就能加密,知道 q就能解密。
而这里的p就是公钥,q就是私钥。
用公钥加密过的密文只有用私钥才能解密。

加密解密公式
而且更妙的是。
p和q其实在公式里位置是可以互换的,所以反过来说“用私钥加密过的密文,只有公钥才能解密”,也是ok的。而这种操作,就是常说的验证数字签名。
这就像以前古装电视剧里,经常有这么个剧情,两个失散多年的亲人,各自身上带有一块碎成两瓣的玉佩。哪天他们发现两块玉佩裂痕正好可以拼在一起,那就确认了对方就是自己失散多年的好大儿。
这两块碎玉,就有点公钥和私钥的味道。

公钥和私钥的关系
原理大家知道这么多其实就够了。
看到这里,我们就能回答下面这个问题了。
为什么用公钥加密,却不能用公钥解密?
因为大数取模运算是不可逆的,因此他人无法暴力解密。但是结合欧拉定理,我们可以选取出合适的p(公钥), q(私钥), N(用于取模的大数),让原本不可逆的运算在特定情况下,变得有那么点“可逆”的味道。数学原理决定了我们用公钥加密的数据,只有私钥能解密。反过来,用私钥加密的数据,也只有公钥能解密。
从数学原理也能看出,公钥和私钥加密是安全的,但这件事情的前提是建立在"现在的计算机计算速度还不够快"这个基础上。因此,如果有一天科技变得更发达了,我们变成了更高维度的科技文明,可能现在的密文就跟明文没啥区别了。
了解了对称加密和非对称加密之后,我们就可以聊聊HTTPS的加密原理了。
HTTPS的加密原理
如果你在公司内网里做开发,并且写的代码也只对内网提供服务。那么大概率你的服务是用的HTTP协议。
但如果哪天你想让外网的朋友们也体验下你的服务功能,那就需要将服务暴露到外网,而这时候如果还是用的HTTP协议,那信息的收发就会是明文,只要有心人士在通讯链路中任意一个路由器那抓个包,就能看到你HTTP包里的内容,因此很不安全。
为了让明文,变成密文,我们需要在HTTP层之上再加一层TLS层,目的就是为了做个加密。这就成了我们常说的HTTPS。

TLS其实分为1.2和1.3版本,目前主流的还是1.2版本,我们以它为例,来看下HTTPS的连接是怎么建立的。
HTTPS 握手过程
首先是建立TCP连接,毕竟HTTP是基于TCP的应用层协议。
在TCP成功建立完协议后,就可以开始进入HTTPS的加密流程。
总的来说。整个加密流程其实分为两阶段。

加密的两阶段
第一阶段是TLS四次握手,这一阶段主要是利用非对称加密的特性各种交换信息,最后得到一个"会话秘钥"。
第二阶段是则是在第一阶段的"会话秘钥"基础上,进行对称加密通信。
我们先来看下第一阶段的TLS四次握手是怎么样的。

HTTPS流程
第一次握手:
-
•
Client Hello:是客户端告诉服务端,它支持什么样的加密协议版本,比如TLS1.2,使用什么样的加密套件,比如最常见的RSA,同时还给出一个客户端随机数。
第二次握手:
-
•
Server Hello:服务端告诉客户端,服务器随机数 + 服务器证书 + 确定的加密协议版本(比如就是TLS1.2)。
第三次握手:
-
•
Client Key Exchange: 此时客户端再生成一个随机数,叫pre_master_key。从第二次握手的服务器证书里取出服务器公钥,用公钥加密pre_master_key,发给服务器。 -
•
Change Cipher Spec: 客户端这边已经拥有三个随机数:客户端随机数,服务器随机数和pre_master_key,用这三个随机数进行计算得到一个"会话秘钥"。此时客户端通知服务端,后面会用这个会话秘钥进行对称机密通信。 -
•
Encrypted Handshake Message:客户端会把迄今为止的通信数据内容生成一个摘要,用"会话秘钥"加密一下,发给服务器做校验,此时客户端这边的握手流程就结束了,因此也叫Finished报文。
第四次握手:
-
•
Change Cipher Spec:服务端此时拿到客户端传来的pre_master_key(虽然被服务器公钥加密过,但服务器有私钥,能解密获得原文),集齐三个随机数,跟客户端一样,用这三个随机数通过同样的算法获得一个"会话秘钥"。此时服务器告诉客户端,后面会用这个"会话秘钥"进行加密通信。 -
•
Encrypted Handshake Message:跟客户端的操作一样,将迄今为止的通信数据内容生成一个摘要,用"会话秘钥"加密一下,发给客户端做校验,到这里,服务端的握手流程也结束了,因此这也叫Finished报文。
短短几次握手,里面全是细节,没有一处是多余的。
我们一个个来解释。
因为大家肯定已经很晕了,所以我会尽量用简短的语句,来解释下面几个问题。
HTTPS到底是对称加密还是非对称机密?
都用到了。前期4次握手,本质上就是在利用非对称加密的特点,交换三个随机数。
目的就是为了最后用这三个随机数生成对称加密的会话秘钥。后期就一直用对称机密的方式进行通信。

对称加密还是非对称加密
为什么不都用非对称加密呢?
因为非对称加密慢,对称加密相对来说快一些。
第二次握手里的服务器证书是什么?怎么从里面取出公钥?
服务器证书,本质上是,被权威数字证书机构(CA)的私钥加密过的服务器公钥。

服务器证书是什么
上面提到过,被私钥加密过的数据,是可以用公钥来解密的。而公钥是任何人都可以得到的。所以第二次握手的时候,客户端可以通过CA的公钥,来解密服务器证书,从而拿到藏在里面的服务器公钥。

用CA公钥解密证书
看起来好像有点多此一举?
那么问题来了。
为什么我不能只传公钥,而要拿CA的私钥加密一次再传过去?
反过来想想,如果只传公钥,公钥就有可能会在传输的过程中就被黑客替换掉。然后第三次握手时客户端会拿着假公钥来加密第三个随机数 pre_master_key,黑客解密后自然就知道了最为关键的 pre_master_key。又因为第一和第二个随机数是公开的,因此就可以计算出"会话秘钥"。
所以需要有个办法证明客户端拿到的公钥是真正的服务器公钥,于是就拿CA的私钥去做一次加密变成服务器证书,这样客户端拿CA的公钥去解密,就能验证是不是真正的服务器公钥。
那么问题又又来了
怎么去获得CA的公钥?
最容易想到的是请求CA的官网,获取公钥。但全世界要上网的人那么多,都用去请求CA官网的话,官网肯定顶不住。
考虑到能颁发证书的CA机构可不多,因此对应的CA公钥也不多,把他们直接作为配置放到操作系统或者浏览器里,这就完美解决了上面的问题。

CA公钥内置于操作系统或浏览器中
别人就拿不到你这三个随机数?
这三个随机数,两个来自客户端,一个来自服务端。第一次和第二次握手里的客户端随机数和服务端随机数,都是明文的。只要有心,大家都能拿到。
但第三个随机数 pre_master_key 则不行,因为它在客户端生成后,发给服务器之前,被服务器的公钥加密过,因此只有服务器本器才能用私钥进行解密。就算被别人拿到了,没有服务器的私钥,也无法解密出原文。
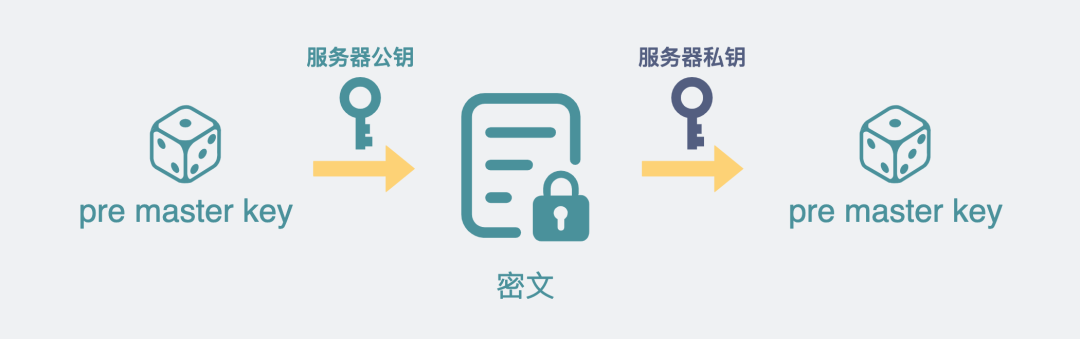
pre_master_key的加密解密
为什么要用三个随机数?而不是一个或两个?

三个随机数生成对称秘钥
看上去第三个随机数 pre_master_key才是关键,另外两个看起来可有可无?
确实,就算没有另外两个,也并不影响加密功能。之所以还要两个随机数,是因为只有单个 pre_master_key随机性不足,多次随机的情况下有可能出来的秘钥是一样的。但如果再引入两个随机数,就能大大增加"会话秘钥"的随机程度,从而保证每次HTTPS通信用的会话秘钥都是不同的。
为什么第三和第四次握手还要给个摘要?
第三和第四次握手的最后都有个 Finished报文,里面是个摘要。
摘要,说白了就是对一大段文本进行一次hash操作。目的是为了确认通信过程中数据没被篡改过。
第三次握手,客户端生成摘要,服务端验证,如果验证通过,说明客户端生成的数据没被篡改过,服务端后面才能放心跟客户端通信。
第四次握手,则是反过来,由服务端生成摘要,客户端来验证,验证通过了,说明服务端是可信任的。
那么问题叒来了。
为什么要hash一次而不是直接拿原文进行对比?
这是因为原文内容过长,hash之后可以让数据变短。更短意味着更小的传输成本。

摘要算法
这个过程中到底涉及了几对私钥和公钥?
两对。
服务器本身的公钥和私钥:在第二次握手中,服务器将自己的公钥(藏在数字证书里)发给客户端。第三次握手中用这个服务器公钥来加密第三个随机数 pre_master_key。服务器拿到后用自己的私钥去做解密。
CA的公钥和私钥:第二次握手中,传的数字证书里,包含了被CA的私钥加密过的服务器公钥。客户端拿到后,会用实现内置在操作系统或浏览器里的CA公钥去进行解密。
总结
-
• 大数取模运算是不可逆的,因此他人无法暴力解密。但是结合欧拉定理,我们可以选取出合适的p(公钥), q(私钥), N(用于取模的大数),让原本不可逆的运算在特定情况下,变得有那么点“可逆”的味道。数学原理决定了我们用公钥加密的数据,只有私钥能解密。反过来,用私钥加密的数据,也只有公钥能解密。
-
• HTTPS相当于HTTP+TLS,目前主流的是TLS1.2,基于TCP三次握手之后,再来TLS四次握手。
-
• TLS四次握手的过程中涉及到两对私钥和公钥。分别是服务器本身的私钥和公钥,以及CA的私钥和公钥。
-
• TLS四次握手背起来会挺难受的,建议关注三个随机数的流向,以此作为基础去理解,大概就能记下来了。