目录

题目：

题目描述：

思路：

AC代码：

---

题目：

题目描述：

zcy数：（形如：11，1221，103301）

①是回文数

②数位个数是偶数

给你两个整数 k 和 p ，问前 k 小的 zcy 数之和对 p 取模是多少？

思路：

分析一下 zcy 数我们会发现，因为偶数个数位的性质，我们可以从中间劈成两半，在相同数位的情况下，一个左半边只存在一种相应的右半边才能满足 zcy 的回文条件。所以 zcy 数的大小只由左半边来决定。

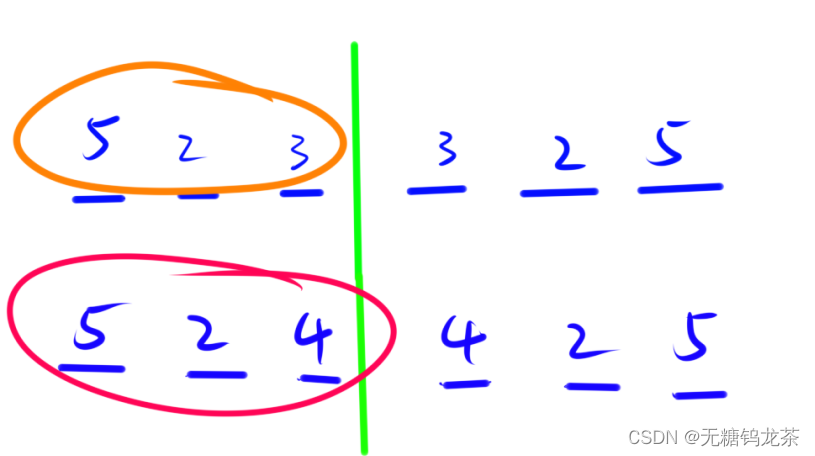
所以我们可以让左半边从 1 开始，逐个递升到 k 。每次依照左半边复现右半边，再将其加到总和里面和取模即可。

值得一提的是这里的小技巧，可以先用  to_string 函数 将左半边转化成字符串，然后用 reverse 函数调换字符串顺序获得右半边样子的字符串，然后再用 stoll函数 （string to long long）函数将字符串转换为数，再进行加和计算会方便很多.....

思路有了，具体操作请看AC代码

AC代码：

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const int N = 2e5 + 5;

void solve()
{
	ll k, p;
	cin >> k >> p;

	ll sum = 0;
	for (int i = 1; i <= k; i++)
	{
		ll temp = 1;//左半边需要乘上的倍数
		
		string s;
		s = to_string(i);
		reverse(s.begin(), s.end());

		for (int i = 0; i < s.size(); i++)
			temp *= 10;
		sum = (sum + i * temp + stoll(s)) % p;
	}
	cout << sum << '\n';
}

int main()
{
	std::ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t = 1;
	while (t--)
		solve();
	return 0;
}