数据结构与算法-堆

news2024/11/19 6:17:58

什么堆
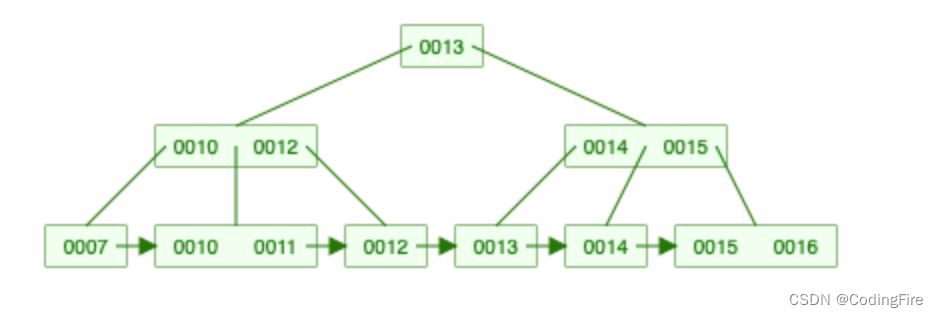
堆是一种特殊的数据结构，是最高效的优先级队列。可以被看作是一颗完全的二叉树表达的数组对象。

堆的定义
1、必须是一颗完全二叉树
完全二叉树就是子节点必须从左到右都是完整的，没有缺失。
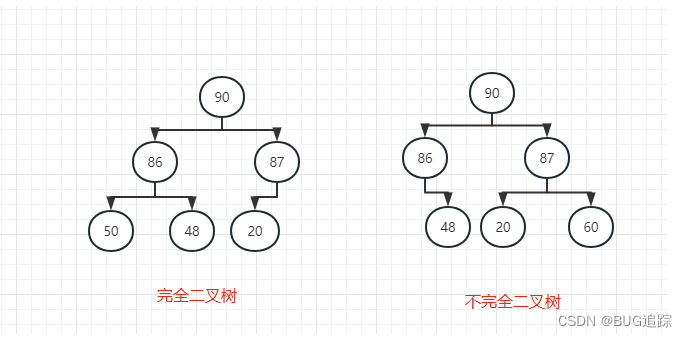
在这里插入图片描述

2、用数组表示看作完全二叉树的堆
假设：当前节点索引为 index
则：
左子节点索引 = 2index+1
右子节点索引 = 2index+2
父节点索引 = （index-1）/2

3、每个节点元素大于或等于其所有子节点大小

堆的时间复杂度
1、n个节点的堆，其根节点为深度0，则第i深度有2^i个元素，构建堆的时间复杂度为O(n)
2、n个节点的深度为logn，插入和删除元素后需要堆元素进行上下交换，故时间复杂度都为O(logn)

优先级队列 VS 堆
优先级队列删除操作时间复杂度为 O(1)，插入操作必须保证顺序时间复杂度为 O(n)
由于n个节点的树高度为 logn,在新增和删除数据需要上下移动元素，故时间复杂度都为 O(logn)

小试牛刀
本次我们讨论新增删除最大堆元素，其他操作较为简单不做讨论
1、提供看作完全二叉树数据结构的工具类
工具类提供增加和删除数据方法

/**
 * 最大堆
 * @author senfel
 * @version 1.0
 * @date 2022/12/28 8:59
 */
public class HeapDemo {

    /**
     * 数组
     */
    private Node[] array;
    /**
     * 下一次插入的索引地址
     */
    private int nextIndex;
    /**
     * 最大容量
     */
    private int maxSize;

    public HeapDemo(int maxSize) {
        this.maxSize = maxSize;
        //默认起始位置作为待插入位置
        this.nextIndex=0;
        this.array = new Node[maxSize];
    }



    /**
     * 新增数据
     * 默认插入最末尾节点，然后往上移动找到适合的位置
     * @param data
     * @author senfel
     * @date 2022/12/28 9:05
     * @return java.lang.Boolean
     */
    public Boolean insert(int data){
        if(nextIndex > maxSize-1){
            //数据组已满
            return false;
        }
        Node node = new Node(data);
        //默认插入到堆末尾
        array[nextIndex] = node;
        //为满足最大堆，数据往上移动找到具体的位置
        elementUp(nextIndex);
        //设置下一个待插入节点
        nextIndex++;
        return true;
    }


    /**
     * 移除根节点数据
     * @author senfel
     * @date 2022/12/28 9:45
     * @return java.lang.Boolean
     */
    public Boolean remove(){
        if(nextIndex == 0){
            return false;
        }
        //将根节点数据重置为末尾节点元素，达到删除根节点效果
        array[0] = array[--nextIndex];
        //被重置的根节点需要往下移动调整位置以满足最大堆
        elementDowm(0);
        //由于末尾元素被移动需要重置为空
        array[nextIndex] = null;
        return true;
    }





    /**
     * 往上移动元素满足最大堆
     * @param index
     * @author senfel
     * @date 2022/12/28 9:08
     * @return void
     */
    private void elementUp(int index) {
        //缓存当前节点数据
        Node temp = array[index];
        //获取当前节点父节点索引
        int parentIndex = (index-1)/2;
        //循环到根节点 并且 父节点不小于子节点 结束
        while (index > 0 && array[index].getData() > array[parentIndex].getData()){
            //父节点移动到当前节点 将当前节点重置为父节点数据
            array[index] = array[parentIndex];
            //将当前节点重置为父节点位置
            index = parentIndex;
            //继续往上找到当前节点父节点
            parentIndex = (index -1)/2;
        }
        //当前节点数据写入
        array[index] = temp;
    }


    /**
     * 往下移动元素满足最大堆
     * @param index
     * @author senfel
     * @date 2022/12/28 9:49
     * @return void
     */
    private void elementDowm(int index) {
        //根节点数据缓存
        Node temp = array[index];
        //找到最后一个节点结束循环
        //只要父节点索引 大于 最后一个父节点索引即可
        while (index <= (nextIndex -1)/2){
            //获取当前节点左右子节点索引
            int leftIndex = 2*index +1;
            int rightIndex = 2*index +2;
            int currentIndex = 0;
            if(leftIndex < nextIndex && array[leftIndex].getData() > array[rightIndex].getData()){
                //左节点数据大于右节点
                currentIndex = leftIndex;
            }else{
                currentIndex = rightIndex;
            }
            if(temp.getData() >= array[currentIndex].getData()){
                //如果当前节点大于等于子节点 则停止移动
                break;
            }
            //子节点移动到当前节点 将当前节点重置为子节点数据
            array[index] = array[currentIndex];
            index = currentIndex;
        }
        //当前节点赋值
        array[index] = temp;
    }


    @Data
    private class Node{
        /**
         * 数据
         */
        private int data;

        public Node(int data) {
            this.data = data;
        }
    }
}

2、新增测试方法
测试方法提供新增、删除元素

public static void main(String[] args) {
        HeapDemo heap = new HeapDemo(10);
        heap.insert(100);
        heap.insert(90);
        heap.insert(98);
        heap.insert(80);
        heap.insert(88);
        heap.insert(91);
        heap.insert(97);
        heap.insert(78);
        heap.insert(79);
        heap.insert(87);
        System.err.println(Arrays.toString(heap.array));
        heap.remove();
        System.err.println(Arrays.toString(heap.array));
        heap.remove();
        System.err.println(Arrays.toString(heap.array));
}

3、查看测试结果并提供图示
3.1 向堆新增10个元素
算法原理为：
每次新增的元素放置在堆底部，然后依次比较父节点元素大小，如果父节点小于子节点则需要移动位置以满足最大堆。
数据结果为：

[HeapDemo.Node(data=100), HeapDemo.Node(data=90), HeapDemo.Node(data=98), HeapDemo.Node(data=80), HeapDemo.Node(data=88), HeapDemo.Node(data=91), HeapDemo.Node(data=97), HeapDemo.Node(data=78), HeapDemo.Node(data=79), HeapDemo.Node(data=87)]

完全二叉树模拟图：
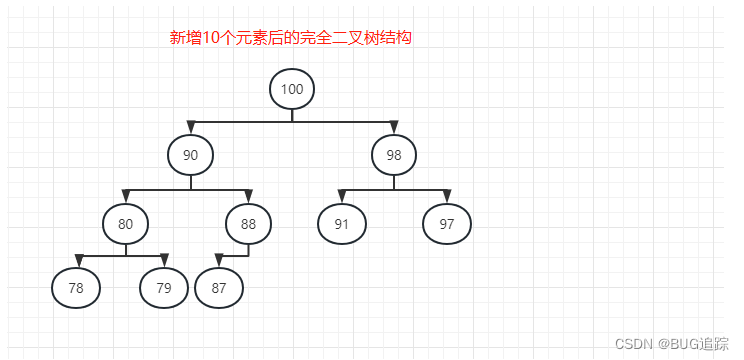
在这里插入图片描述

3.2 向堆删除顶部元素100
算法原理为：
每次删除将最底部元素赋值给顶部元素，达到删除顶部元素效果。然后依次比较子节点元素大小，如果子节点大于父节点则需要移动元素以满足最大堆，最后重置底部元素为空即可。
数据结果为：

[HeapDemo.Node(data=98), HeapDemo.Node(data=90), HeapDemo.Node(data=97), HeapDemo.Node(data=80), HeapDemo.Node(data=88), HeapDemo.Node(data=91), HeapDemo.Node(data=87), HeapDemo.Node(data=78), HeapDemo.Node(data=79), null]

完全二叉树模拟图：
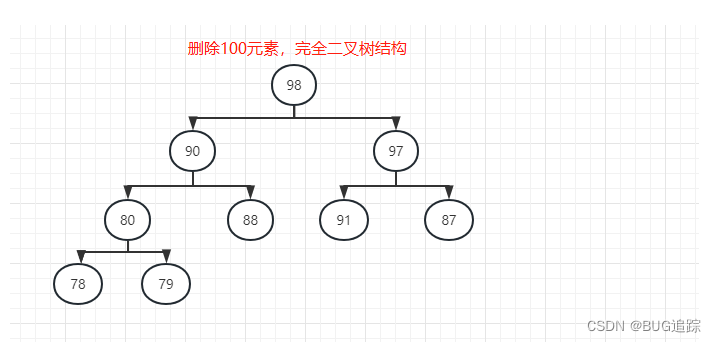
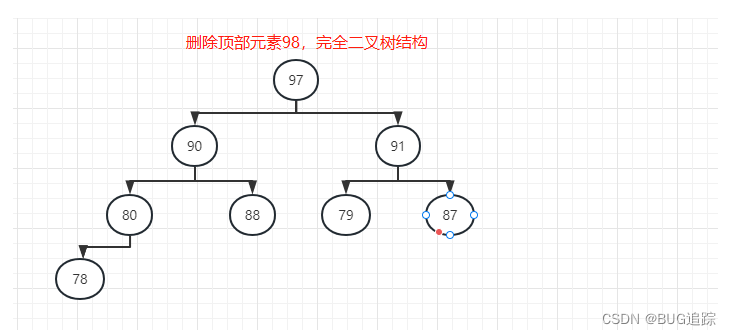
在这里插入图片描述

3.3 向堆删除顶部元素98
算法原理为：
每次删除将最底部元素赋值给顶部元素，达到删除顶部元素效果。然后依次比较子节点元素大小，如果子节点大于父节点则需要移动元素以满足最大堆，最后重置底部元素为空即可。
数据结果为：

[HeapDemo.Node(data=97), HeapDemo.Node(data=90), HeapDemo.Node(data=91), HeapDemo.Node(data=80), HeapDemo.Node(data=88), HeapDemo.Node(data=79), HeapDemo.Node(data=87), HeapDemo.Node(data=78), null, null]

完全二叉树模拟图：
在这里插入图片描述