💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

2.1 两万辆电动车

2.2 一万辆电动车

🌈3 Matlab代码实现

🎉4 参考文献

---

💥1 概述

 计算机模拟中的蒙特卡洛法也被称为随机抽样技术或统计检验方法，该方法最重要的特点是它是一种基于概率统计理论的方法。随着科学技术的发展和电子计算机的发明，蒙特卡洛法以其描述物理发展特点和物理实验过程的优点，在各个领域得到了广泛的应用。
蒙特卡洛法将目前所解决的问题当作是一种随机事件的概率，也可以将其看作是随机事件的期望值。按照某种实验的方式，通过某随机事件的出现频率来计算该事件的概率，或者是求得其数字特征，将实验所得的结论作为问题的解。采用蒙特卡洛法，在进行模拟计算时一般按照以下步骤进行,若所需解决的问题存在随机性特征，则就能将这个概率过程更加准确的描述和模拟，若问题并不具备随机性，反而是一种确定性问题，就必须认为建立相应的概率过程，而某些相关参量恰好就是该问题的解，整个过程就是将某问题的确定性改造为随机性。
   在建立这种概率模型之后，可将不同的概率模型视为有不同类型的概率分布组成，由此就可获得己知概率分布的随机变量，如此就能成为可以进行蒙特卡罗方法模拟实验的主要方式，所以这种方法也是一种随机抽样。蒙特卡罗模拟的实现便是在已知概率分布所导致的随机数基础上进行的。
一般在建立这种概率模型后可以从中抽样，也就是实现模拟实验，在此之后还应当将其中某个随机变量确定下来，即所需解决问题的解，被称为无偏估计。通过获得多种估计量，例如方差等，就能够通过模拟方法获得问题的解。
   对于本文的研究,依据不同用途电动汽车影响因素的分布函数和设定参数,采用蒙特卡洛法，对各用途电动汽车的日行驶里程、起始充电时间概率分布参数进行随机抽样，计算初始荷电状态和和充电所需时长，进而预测得出各类型的电动汽车充电负荷曲线，最后通过叠加各用途电动汽车的充电负荷曲线得出总的充电负荷曲线。
 

知识回顾：

基于蒙特卡洛法的规模化电动车有序充放电及负荷预测（Python&Matlab实现）

（Matlab实现）基于蒙特卡诺和拉格朗日乘子法的电动车调度【有序、无序充放电】

电动汽车有序无序充放电的优化调度（Matlab代码实现）

基于蒙特卡洛的电动车有序充放电（Matlab代码实现）

基于蒙特卡洛的大规模电动汽车充电行为分析（Matlab代码实现）

(Matlab实现)基于蒙特卡洛模拟的大规模电动车充电模型

基于蒙特卡洛法的规模化电动汽车充电负荷预测（Python&Matlab实现）

电动汽车电池换电站选址与定容（Matlab代码实现）

基于蒙特卡诺的电动汽车对电网影响（数据+Matlab代码）

模拟大规模电动车充电行为（Matlab实现）

📚2 运行结果

2.1 两万辆电动车

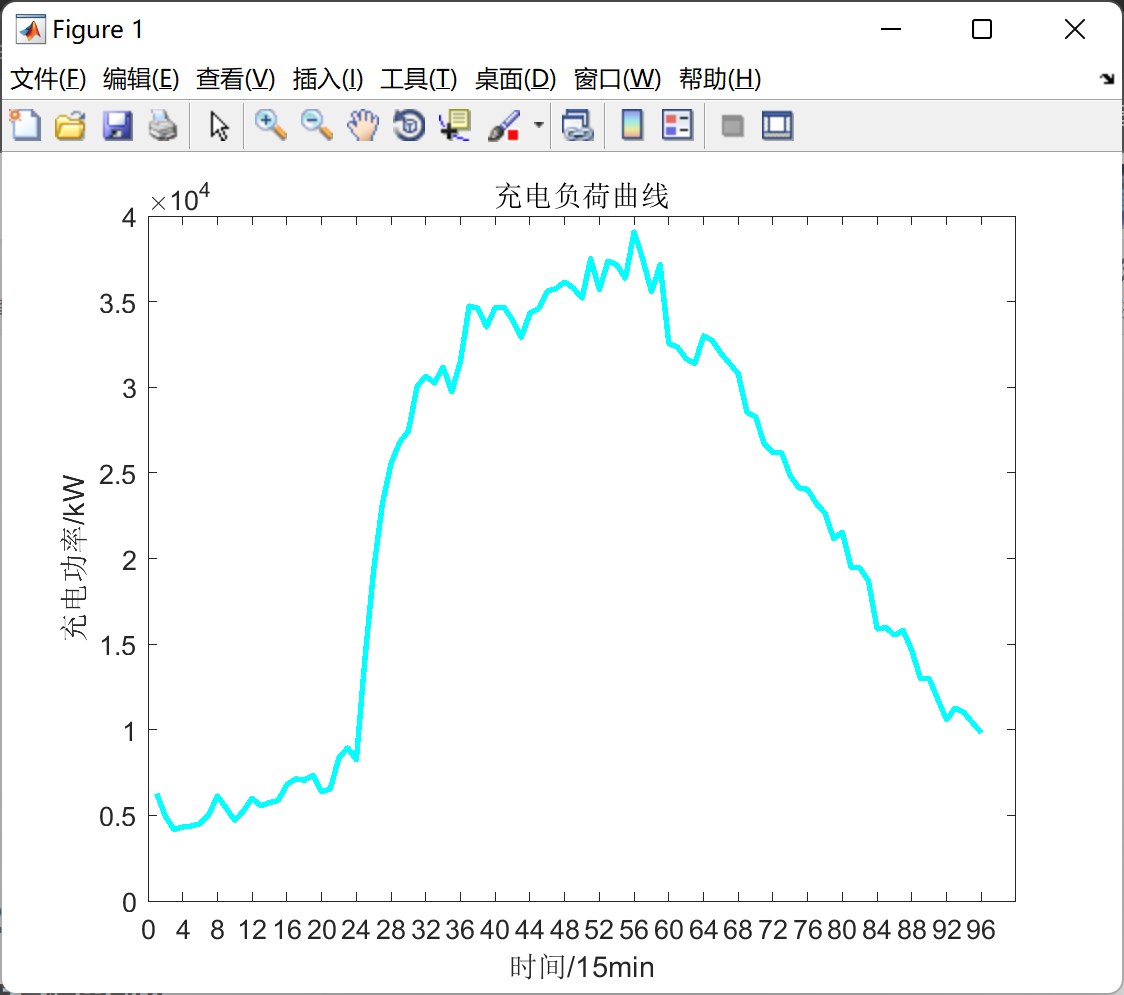
2.2 一万辆电动车

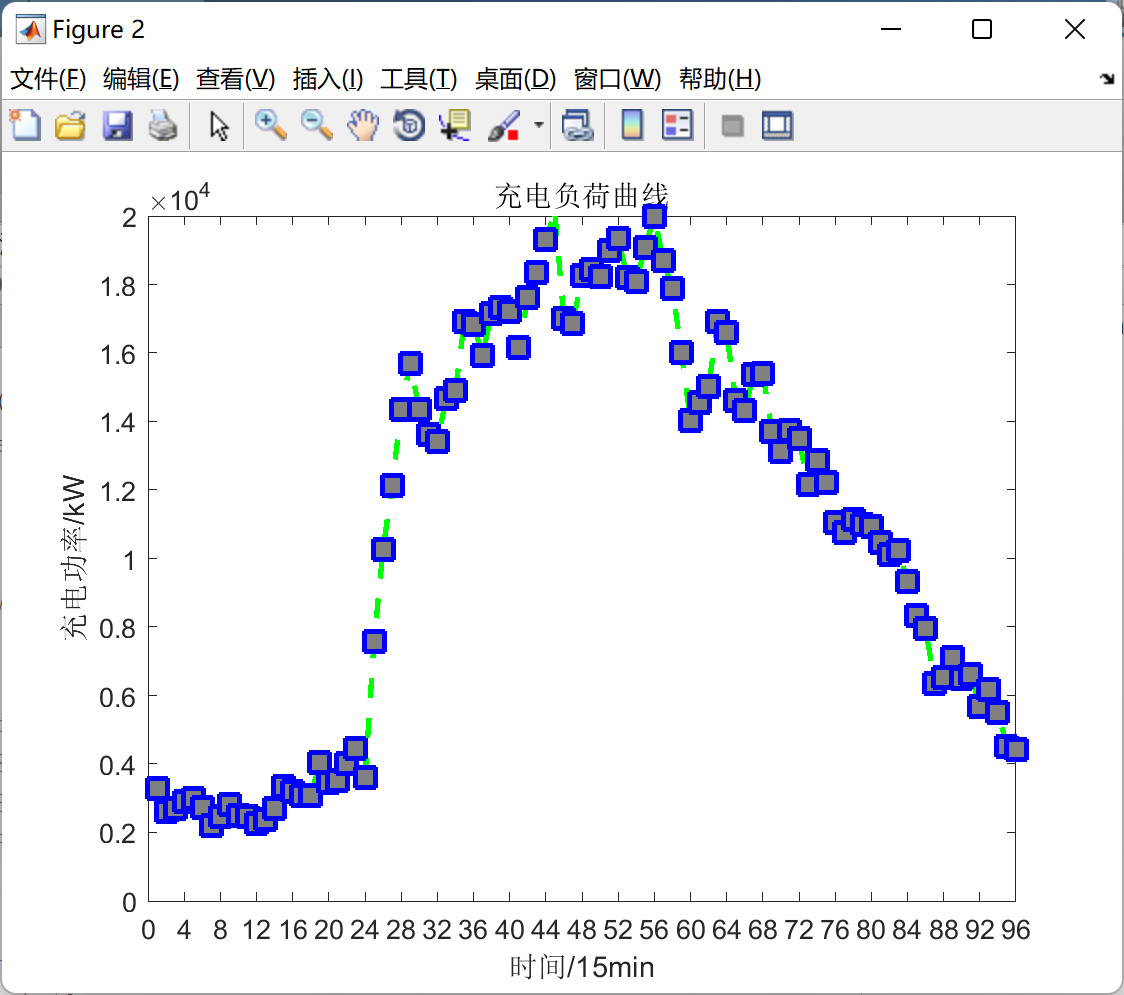
 部分代码：

P=rand();%随机生成一个取值范围在[0-1]的数字
if 0<=P&&P<rate(1)
%     char_i=1;
    P_hi=(P_h(1,1)+P_h(1,2))/2;   %选择第一种充电方式
%     P_rate=P;
elseif rate(1)<=P&&P<(rate(1)+rate(2))
%     P_rate=P;
%     char_i=2;
    P_hi=(P_h(2,1)+P_h(2,2))/2;  %选择第二种充电方式
else
%     P_rate=P;
%     char_i=3;
    P_hi=(P_h(3,1)+P_h(3,2))/2;%选择第三种充电方式
end

P=rand();%随机生成一个取值范围在[0-1]的数字
if 0<=P&&P<rate(1)
%     char_i=1;
    P_hi=(P_h(1,1)+P_h(1,2))/2;   %选择第一种充电方式
%     P_rate=P;
elseif rate(1)<=P&&P<(rate(1)+rate(2))
%     P_rate=P;
%     char_i=2;
    P_hi=(P_h(2,1)+P_h(2,2))/2;  %选择第二种充电方式
else
%     P_rate=P;
%     char_i=3;
    P_hi=(P_h(3,1)+P_h(3,2))/2;%选择第三种充电方式
end

🌈3 Matlab代码实现

🎉4 参考文献

部分理论来源于网络，如有侵权请联系删除。