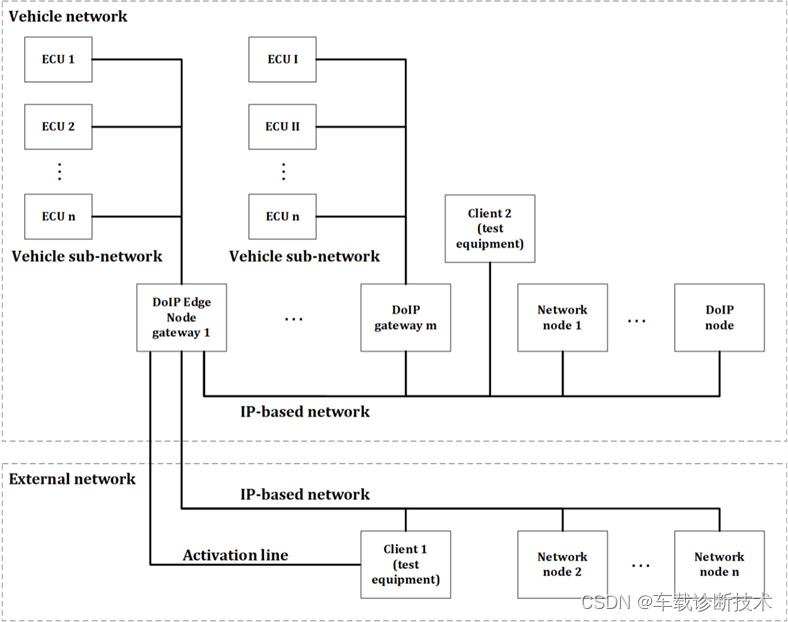
感知机(perceptron)为神经网络的起源算法。感知机接受多个输入信号,输出一个信号。感知机信号只有0和1。

在上图的感知机中,x1和x2两个输入信号会分别乘以其对应权重(weight) w1和w2,传入神经元。神经元计算传来信号综合,当总和超过某一阈值时输出1,否则输出0。阈值一般用θ表示
为了后续了解神经网络,我们把θ改为-b,其中b被称为偏置。感知机计算输入信号和偏置和,如果和大于0输出1,否则输出0
用公式表示如下:

2 用感知机实现逻辑电路
与门:
与门只有在输入都为1时才输出1。利用感知机实现只需要使每一个单独权重小于阈值,但权重和大于阈值
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
与非门:
与非门和与门相反,在输入都为1时输出0,否则输出1。对与门的权重和偏置都取负数即实现与非门
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
或门:
或门只要有一个输入为1即输出1,在两个输入都为0是返回0。实现或门可以使每一个权重值都大于阈值
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
异或门:
异或门在两个输入不同时返回1,输入相同时返回0
使用单层感知机无法实现异或门。因为感知机只能表示线性空间。感知机函数 b + w1x1 + w2x2 = 0在图像上既是一条斜率为 -w1/w2, y交点为b的直线。直线下方值为0,直线上方值为1。在如图的或门中,(0,0)位于直线下方取值1,而(1,0),(0,1),(1,1)取值1

但是,对于异或门,我们无法通过一条直接将(0,0),(1,1)和(1,0)(0,1)分开,只能使用如下图的曲线

使用曲线分割空间被称为非线性空间,可以用多层感知机网络实现。通过组合与门,与非门,或门即可实现异或门

def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
理论上来说,感知机可以实现所有类型逻辑门,并可以搭建一个计算机