我们知道拉格朗日函数是用于等式约束的优化问题求解的，然KKT条件是针对含有不等式约束的优化问题的。

首先，我们先给出优化目标：

因此，根据优化目标，我们同样可以构造处拉格朗日函数，并对其进行优化，从而得到如下所示的一般形式的KKT条件。

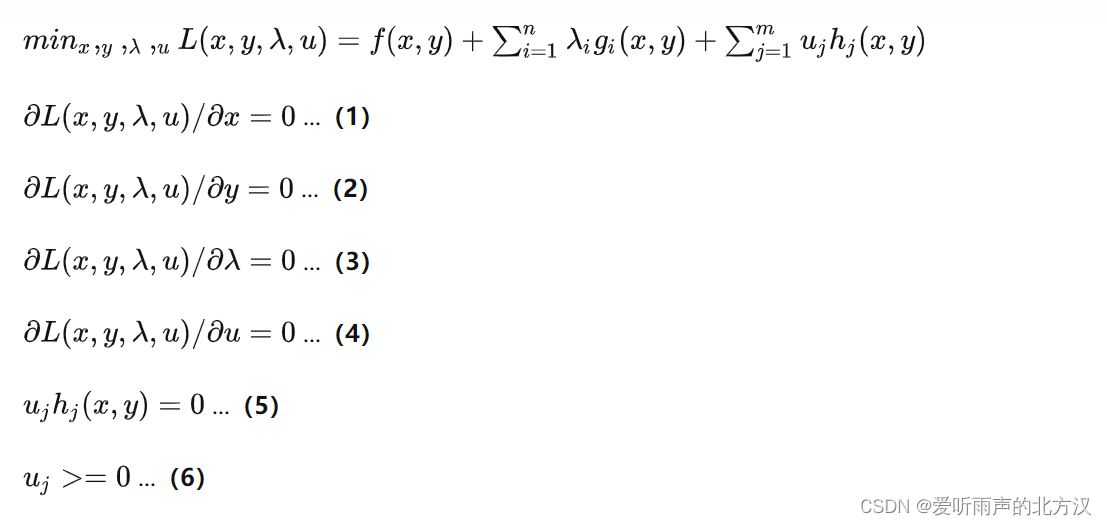
 可以发现，相比等式约束极值的求解方法拉格朗日乘子法，这里由于不等式的约束增加了（5）和（6）两个条件，这个条件如何理解呢：
假设我们已经得到了由约束问题构成的约束集合,那么可能存在着两种可能性：

①最优值出现在可行域内部，此时约束条件不再起作用，因此问题就变成了无约束的极值问题；

②最优解出现在可行域的边界上，此时约束条件起作用，因此问题就变成了等式约束的极值问题。

如果说最优值出现在可行域的内部，那么相当于所有的不等式约束都不起作用，因为即使是没有不等式约束，最优值也会出现在这里，这个时候所有的不等式都不应该出现在优化的目标函数中，即 uj 全为0；

如果说最优值出现在可行域的边界上，那么对应的不等式约束就变成了等式约束，所以就应该有 hj=0 ，同时应该出现在优化的目标函数中，其 uj 不等于0。

总之，由于优化问题的可行域边界可能是由多个不等式约束构成的交集，即对于这些不等式而言都有 hj=0 。而那些并不能构成可行域的边界的不等式约束同样不应该出现在优化目标函数中，所以应该有 uj=0 。所以我们发现无论不等式约束是不是有效约束，因此，总会有 ujhj=0。

就条件（6） 而言， 其主要是因为我们要求一个约束问题的最小值时，如果存在最优值，目标函数和约束条件的梯度应该共线，而我们的KKT条件中标准形式是最小化且不等式约束条件都是<=0的，所以进一步的有目标函数和约束条件梯度反向。

因此，考虑到问题中的可行域是在 g(x)<=0 一侧，而g(x)的梯度是指向大于 0 的一侧，也就是不是可行域的一侧。而求的问题是极小值，所以 f(x) 在交点处的梯度是指向可行域的一侧，也就是说两个梯度一定是相反的。所以也就可以确定这里的系数 uj 一定是大于 0 的。