02、Java 数据结构：时间复杂度与空间复杂度

news2024/10/5 22:24:01

时间复杂度与空间复杂度

1 场景理解
- 1.1 场景1
- 1.2 场景2
- 1.3 场景3
- 1.4 场景4
- 1.5 代码实现
2 时间复杂度
- 2.1 渐进时间复杂度
- 2.2 从基本操作执行次数推导出时间复杂度
- 2.3 两种方法来计算
- 2.4 四个场景的时间复杂度分析
- 2.5 大 O 表达式的优劣
3 空间复杂度
4 时间复杂度和空间按复杂度关系
- 4.1 关系
- 4.2 例子
- 4.3 程序中的应用

1 场景理解

1.1 场景1

给大黄一条长10寸的面包，大黄每3天吃掉1寸，那么吃掉整个面包需要几天？

答案自然是 3 X 10 = 30天。
如果面包的长度是 N 寸呢？
此时吃掉整个面包，需要 3 X n = 3n 天。
如果用一个函数来表达这个相对时间，可以记作 T(n) = 3n。

1.2 场景2

给大黄一条长16寸的面包，大黄每5天吃掉面包剩余长度的一半，第一次吃掉8寸，第二次吃掉4寸，第三次吃掉2寸…那么大黄把面包吃得只剩下1寸，需要多少天呢？

这个问题翻译一下，就是数字16不断地除以2，除几次以后的结果等于1？这里要涉及到数学当中的对数，以2位底，16的对数，可以简写为log16。因此，把面包吃得只剩下1寸，需要 5 X log16 = 5 X 4 = 20 天。
如果面包的长度是 N 寸呢？
需要 5 X logn = 5logn 天，记作 T(n) = 5logn。

1.3 场景3

给大黄一条长10寸的面包和一个鸡腿，大黄每2天吃掉一个鸡腿。那么大黄吃掉整个鸡腿需要多少天呢？

答案自然是2天。因为只说是吃掉鸡腿，和10寸的面包没有关系。
如果面包的长度是 N 寸呢？
无论面包有多长，吃掉鸡腿的时间仍然是2天，记作 T(n) = 2。

1.4 场景4

给大黄一条长10寸的面包，大黄吃掉第一个一寸需要1天时间，吃掉第二个一寸需要2天时间，吃掉第三个一寸需要3天时间…每多吃一寸，所花的时间也多一天。那么大黄吃掉整个面包需要多少天呢？

答案是从1累加到10的总和，也就是55天。
如果面包的长度是 N 寸呢？
此时吃掉整个面包，需要 1+2+3+…+ n-1 + n = (1+n)*n/2 = 0.5n^2 + 0.5n。
记作 T（n） = 0.5n^2 + 0.5n。

1.5 代码实现

上面所讲的是吃东西所花费的相对时间，这一思想同样适用于对程序基本操作执行次数的统计。刚才的四个场景，分别对应了程序中最常见的四种执行方式

场景1： T(n) = 3n，执行次数是线性的

void eat1(int n){
    for(int i=0; i<n; i++){;
        System.out.println("等待一天");
        System.out.println("等待一天");
        System.out.println("吃一寸面包");
    }
}

场景2： T(n) = 5logn，执行次数是对数的

void eat2(int n){
   for(int i=1; i<n; i*=2){     
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("等待一天");
       System.out.println("吃一半面包");
   }
}

场景3： T(n) = 2，执行次数是常量的

void eat3(int n){
   System.out.println("等待一天");
   System.out.println("吃一个鸡腿");
}

场景4： T(n) = 0.5n^2 + 0.5n，执行次数是一个多项式

void eat4(int n){
   for(int i=0; i<n; i++){   
       for(int j=0; j<i; j++){
           System.out.println("等待一天");  
       }
       System.out.println("吃一寸面包");   
   }
}

2 时间复杂度

2.1 渐进时间复杂度

有了基本操作执行次数的函数 T(n)，是否就可以分析和比较一段代码的运行时间了呢？还是有一定的困难
比如算法 A 的相对时间是T(n)= 100n，算法 B 的相对时间是 T(n)= 5n^2，这两个到底谁的运行时间更长一些？这就要看 n 的取值了。所以，这时候有了渐进时间复杂度（asymptotic time complectiy）的概念
官方的定义如下：若存在函数 f(n)，使得当 n 趋近于无穷大时，T(n) / f(n) 的极限值为不等于零的常数，则称 f(n) 是 T(n) 的同数量级函数。记作 T(n) = O(f(n))，称 O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。渐进时间复杂度用大写 O 来表示，所以也被称为大 O 表达式

2.2 从基本操作执行次数推导出时间复杂度

如果程序的运行次数和要处理的量n的大小没有关系，用常数1表示；O(1)
如果程序的运行次数和要处理的量n的大小有关系，只保留关系函数中的最高阶项； O(n^2)
如果最高阶项存在，则省去最高阶项前面的系数。 O(n^2)

2.3 两种方法来计算

事后统计：写出代码，计算时间，不推荐。
事前分析：比较所有语句执行的次数总和，为了方便，仅比较它们的数量级就行

有时候复杂度会受其他数据的影响，会有最坏时间复杂度、平均时间复杂度、最好时间复杂度，一般情况下，只考虑最坏时间复杂度和平均时间复杂度

对于复杂的算法，可以将其分为几个容易估算的部分，然后利用大 O 加法法则和乘法法则，计算算法的复杂度：

加法法则取时间复杂度最大的一个
乘法法则几个计算出来的最后时间复杂度相乘

2.4 四个场景的时间复杂度分析

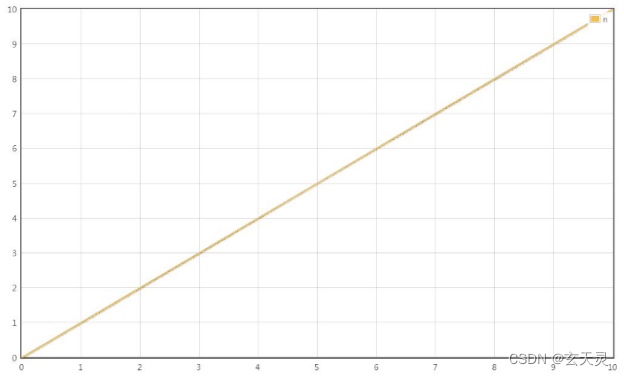
场景1：
T(n) = 3n
最高阶项为3n，省去系数3，转化的时间复杂度为：T(n) = O(n) 大 O 线性阶
在这里插入图片描述
场景2：
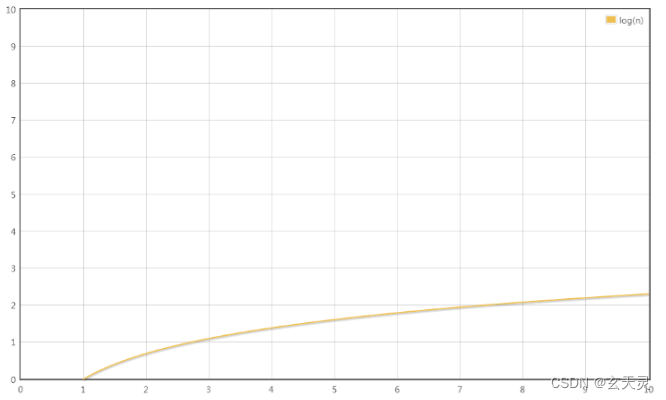
T(n) = 5logn
最高阶项为5logn，省去系数5，转化的时间复杂度为：T(n) = O(logn) 大 O 对数阶

场景3：
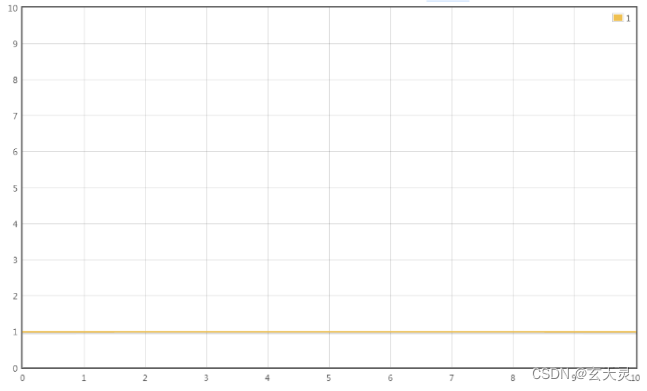
T(n) = 2
只有常数量级，转化的时间复杂度为：T(n) = O(1) 大 O 常数阶
在这里插入图片描述

场景4：
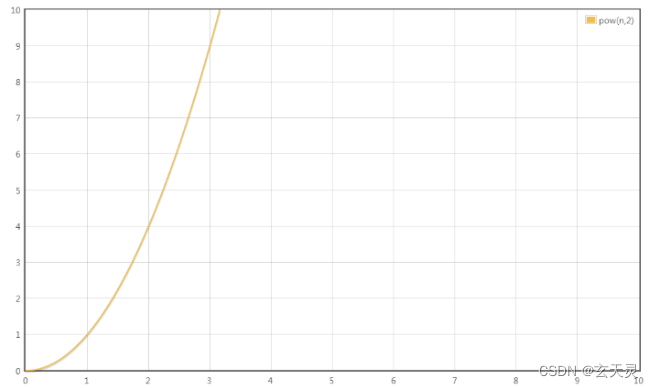
T(n) = 0.5n^2 + 0.5n
最高阶项为 0.5n^2，省去系数0.5，转化的时间复杂度为：T(n) = O(n^2) 大 O 平方阶
在这里插入图片描述

2.5 大 O 表达式的优劣

大O表达式	算法的好坏
O(1)	最好
O(logn)	比较好
O(n)	良好
O(n^2)	不好
O(n^3)	很不好
O(2^n)	很很不好
O(n!)	最不好

例子：

算法A的相对时间规模是 T(n)= 100n*100，时间复杂度是 O(n)
算法B的相对时间规模是 T(n)= 5n^2，时间复杂度是 O(n^2)
随着输入规模 n 的增长，两种算法谁运行更快呢？

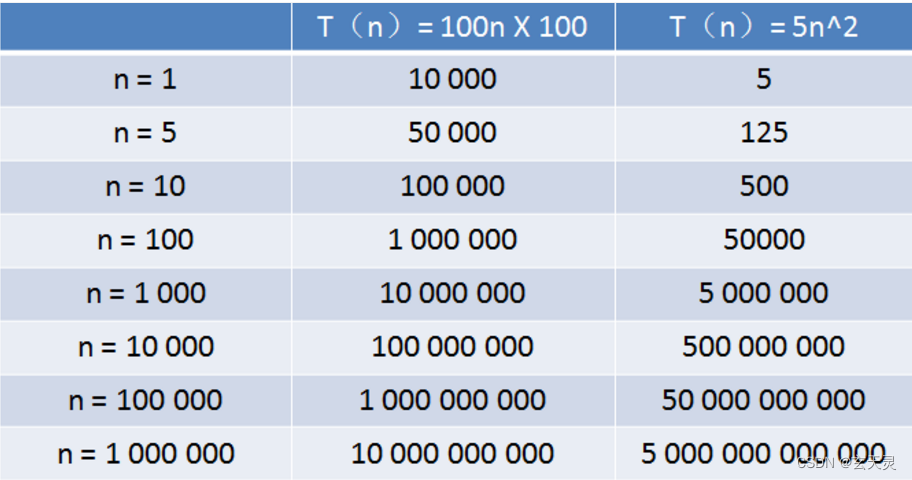
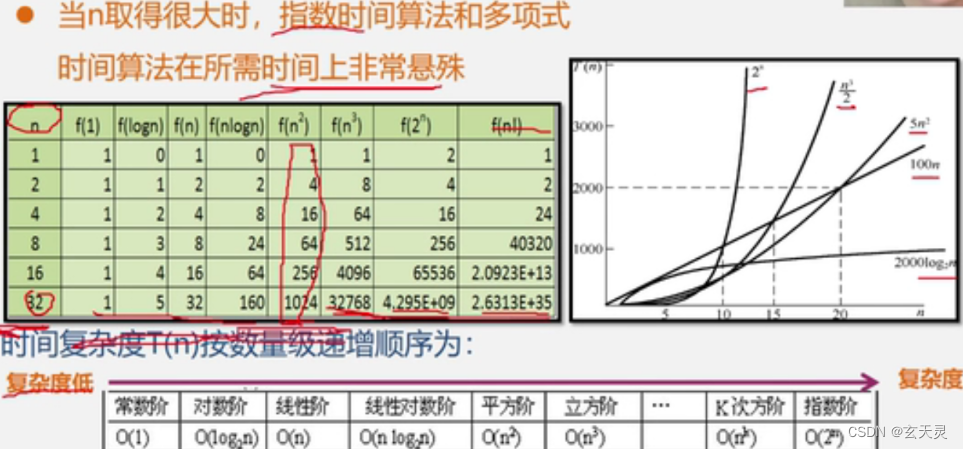
从表格中可以看出，当 n 的值很小的时候，算法 A 的运行用时要远大于算法 B；当 n 的值达到1000左右，算法 A 和算法 B 的运行时间已经接近；当 n 的值越来越大，达到十万、百万时，算法 A 的优势开始显现，算法 B 则越来越慢，差距越来越明显

3 空间复杂度

空间复杂度和时间复杂度很类似，当一个算法的空间复杂度为一个常量，即不随被处理数据量 n 的大小而改变时，可表示为 O(1)；当一个算法的空间复杂度与以2为底的 n 的对数成正比时，可表示为 O(log2n)；当一个算法的空间复杂度与 n 成线性比例关系时，可表示为O(n)…

4 时间复杂度和空间按复杂度关系

4.1 关系

程序的设计中要不就是时间换空间，要不就是用空间去换时间。并且时间和空间是可以进行相互转化的：

对于执行的慢的程序，可以通过消耗内存（即构造新的数据结构）来进行优化
消耗内存的程序，也可以多消耗时间来降低内存的消耗

4.2 例子

//时间换空间
int a = 5;
int b = 10;
a = a+b;//得到a值为15
b = a-b;//得到b值为5
a = a-b;//得到a值为10

//空间换时间
int c = 5;
int d = 10;
int e = c;//得到e为5
c= d;//得到c值为10
d= e;//得到d值为