作者：~小明学编程 

文章专栏：Java数据结构

格言：目之所及皆为回忆，心之所想皆为过往

目录

插入排序

原理

代码实现

算法性能分析

希尔排序

引入

原理

代码

算法分析

选择排序

原理

代码

堆排序

原理

代码

算法分析

冒泡排序

原理

代码

算法分析

---

插入排序

原理

插入排序顾名思义就是通过一个个的插入来实现排序的，首先我们遍历数组，每遍历一个元素，将其值给temp，然后找当前元素的前面一个元素，当我们只有一个元素的时候肯定就是有序的，所以我们一般就从第二个元素开始遍历。我们把i记作当前元素的下标，然后将j=i-1记作其前一个元素的下标。

 这里我们拿从小到大的顺序来做演示，所以当前我们j元素的下标的12，temp为8，当我们的j下标的元素大于temp的时候就将我们的当前元素向后推，也就是 array[j+1] = array[j]，

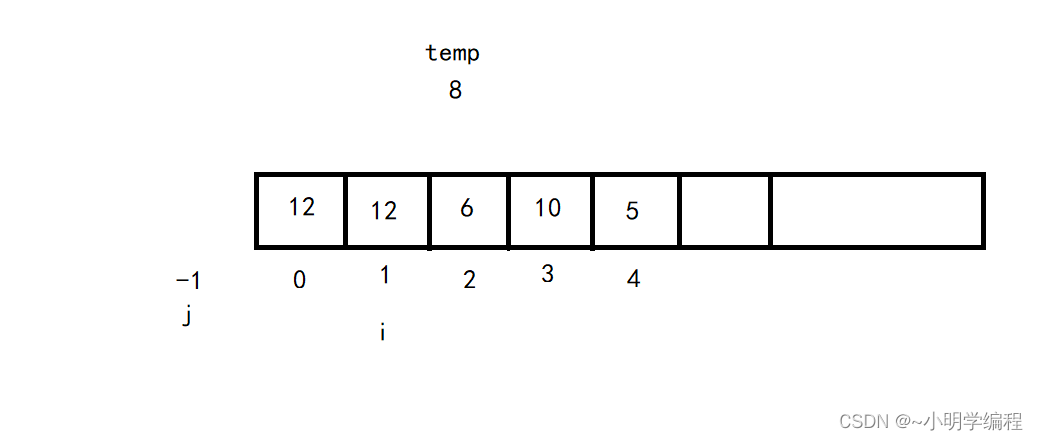
 然后此时我们的j = -1,当j = -1的时候我们退出循环，然后将j+1的位置置为temp也就是8。

 这个时候我们的前两个元素就有序了，然后我们接着进行循环遍历2下标的位置。

依旧如上，因为j所在的位置大于我们的temp，所以将当前的元素向后推，当小于的时候就array[j+1] = temp。

 此时我们的前三个元素已经有序了，然后继续排序，

 array[j]>temp，所以向后推，

 这时我们发现array[j]<temp了，所以直接退出循环，执行array[j+1] = temp。

 此时前面四个元素已经排序完成，最后一个元素同理进行排序。

 最终完成了我们的插入排序。

代码实现

    public static void insertSort(int[] array) {
        for (int i = 1; i < array.length; i++) {
            int temp = array[i];
            int j = i-1;
            for (; j >=0 ; j--) {
                if (array[j] > temp) {
                    array[j+1] = array[j];
                } else {
                    break;
                }
            }
            array[j+1] = temp;
        }
    }

    public static void main(String[] args) {
        int[] array = {12,56,58,23,6,99,56};
        insertSort(array);
        System.out.println(Arrays.toString(array));//[6, 12, 23, 56, 56, 58, 99]
    }

算法性能分析

 算法稳定性：稳定。

重点：根据上表我们可以得出一个结论，对于快速排序来说，当我们的数据越有序，我们排序的速度就越快。

希尔排序

引入

希尔排序是由插入排序引入而来的，前面我们在学习插入排序的时候我们知道其算法的时间复杂度是比较高的，当我们有10000数据的时候最坏情况下的实例化复杂度为100000000，可以看到这个计算量是非常大的，一万就如此当有十万或者一百万个数据的时候就不知道要排到啥时候了。

这个时候我们有一个想法，那就是我们先把这10000个数据分成100份，这样每份就只有100个数据了，当我们再次的去实例化这个复杂度的时候就为100 * 100 * 100 = 1000000，一百万，相比之前的一个亿要好很多了，故而就引出了我们的额希尔排序。

原理

希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数gap，把待排序文件中所有记录分成个gap组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达=1时，所有记录在统一组内排好序。

1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。
 

代码

这里代码的实现是根据其思想写的，但是gap的值我们具体的去找合适的素数，只是通过除2来找出gap的大小。

    public static void shell(int[] array,int gap) {
        for (int i = gap; i < array.length; i++) {
            int temp = array[i];
            int j = i-gap;
            for (; j>=0 ; j-=gap) {
                if (array[j]>temp) {
                    array[j+gap] = array[j];
                } else {
                    break;
                }
            }
            array[j+gap] = temp;
        }
    }
    public static void shellSort(int[] array) {
        int gap = array.length;
        while (gap>1) {
            shell(array,gap);
            gap /= 2;
        }
        shell(array,1);
    }

算法分析

 稳定性：不稳定。

选择排序

原理

其中心思想就是：每一次从无序区间选出最大（或最小）的一个元素，存放在无序区间的最后（或最前），直到全部待排序的数据元素排完。

其实就是我们先要遍历一下我们的数组，当前的下标记作i，然后我们的j = i+1，让我们的j遍历后面的元素，如果当前的元素小于我们j下标的元素（从小到大排序为例）就交换，所以一个内循环结束无序序列最前面的元素就是最小的了。

代码

    public static void selectSort(int[] array) {
        for (int i = 0; i < array.length; i++) {
            boolean flag = true;
            int min = i;
            for (int j = i+1; j < array.length; j++) {
                if (array[j]<array[min]) {
                    min = j;
                    flag = false;
                }
            }
            int ret = array[min];
            array[min] = array[i];
            array[i] = ret;
            if (flag) break;
        }
    }

这里面我们堆代码进行了一些优化，首先就是我们定义了min，就是记录我们最小值的下标，在我们内循环结束后就交换最前面的无序序列和我们的最小值，再而我们定义了一个flag如果我们检测到后面全部都是有序的话，直接退出循环。

时间复杂度	空间复杂度
O(n^2)	O(1)
数据不敏感	数据不敏感

稳定性：不稳定

堆排序

原理

基本原理也是选择排序，只是不在使用遍历的方式查找无序区间的最大的数，而是通过堆来选择无序区间的最大的数。
注意： 排升序要建大堆；排降序要建小堆。

代码

    //堆排序
    public static void heapSort(int[] array) {
        createHeap(array);
        int len = array.length-1;
        while (len>0) {
            swap(array,0,len);
            shiftDown(array,0,len);
            len--;
        }
    }
    //建堆
    public static void createHeap(int[] array) {
        for (int parents = (array.length-1-1)/2; parents >= 0; parents--) {
            shiftDown(array,parents,array.length);
        }
    }
    //向下调整
    public static void shiftDown(int[] array,int parents,int len) {
        int children = parents * 2 + 1;
        while (children < len) {
            if ((children+1)<len && array[children]<array[children+1]) {
                children++;
            }
            if (array[parents] < array[children]) {
                swap(array,children,parents);
                parents = children;
                children = parents * 2 + 1;
            } else {
                break;
            }
        }
    }

排序过程：Heap Sort Visualization (usfca.edu)

算法分析

时间复杂度	空间复杂度
O(n * log(n))	O(1)
数据不敏感	数据不敏感

稳定性：不稳定。

冒泡排序

原理

在无序区间，通过相邻数的比较，将最大的数冒泡到无序区间的最后，持续这个过程，直到数组整体有序。

代码

    //冒泡排序
    public static void bubbleSort(int[] array) {
        for (int i = 0; i < array.length; i++) {
            boolean flag = true;
            for (int j = 0; j < array.length - i - 1; j++) {
                if (array[j]>array[j+1]) {
                    swap(array,j,j+1);
                    flag = false;
                }
            }
            if (flag) break;
        }
    }

算法分析

 稳定性：稳定。