👨‍🎓个人主页：研学社的博客 

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

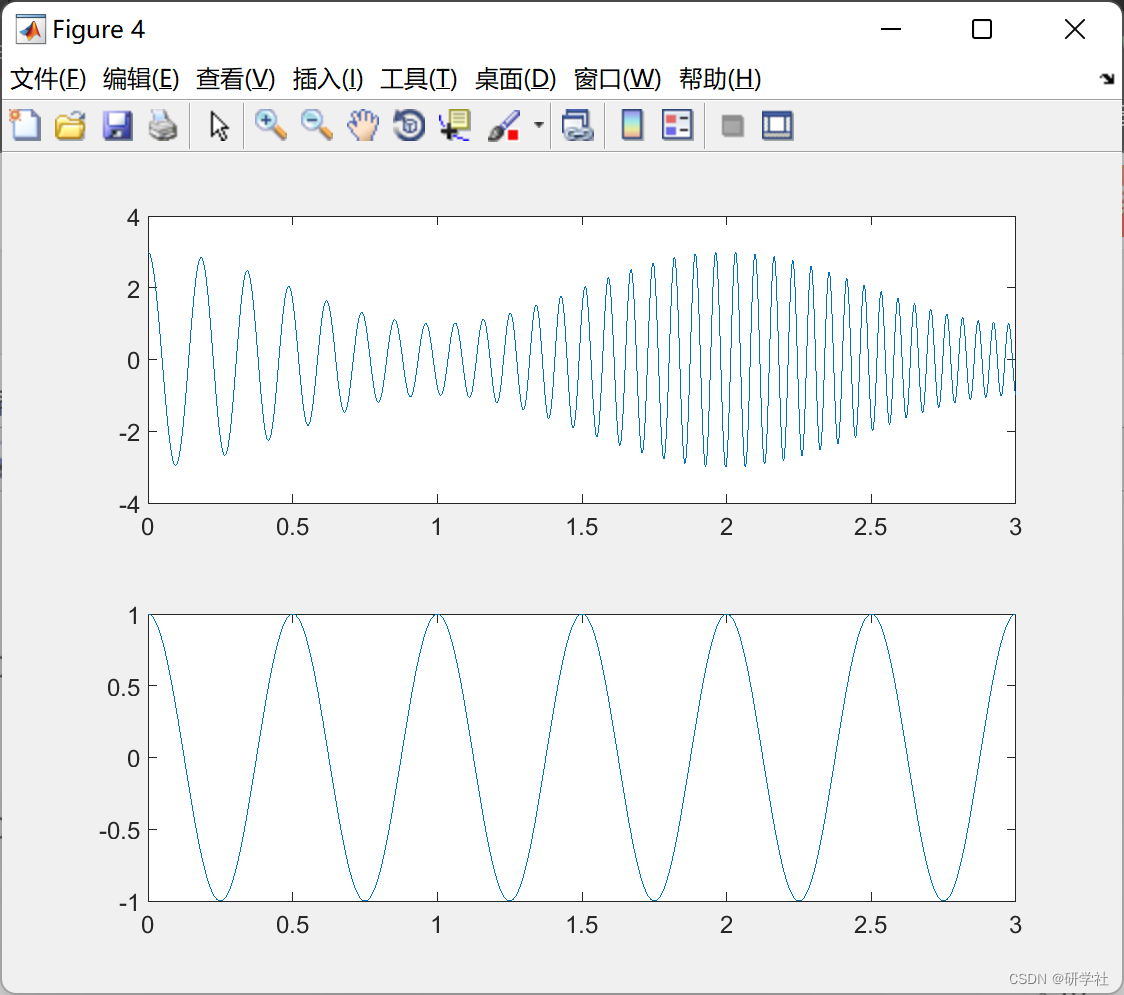
📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

RLMD 是一种改进的局部均值分解，由一组优化策略提供支持。优化策略可以处理LMD中的边界条件、包络估计和筛选停止准则。它同时从混合信号中提取一组单分量信号（称为乘积函数）及其相关的解调信号（即AM信号和FM信号），与其他自适应信号处理方法（如EMD）相比，这是最吸引人的特征。RLMD可用于时频分析。

📚2 运行结果

 

 

 

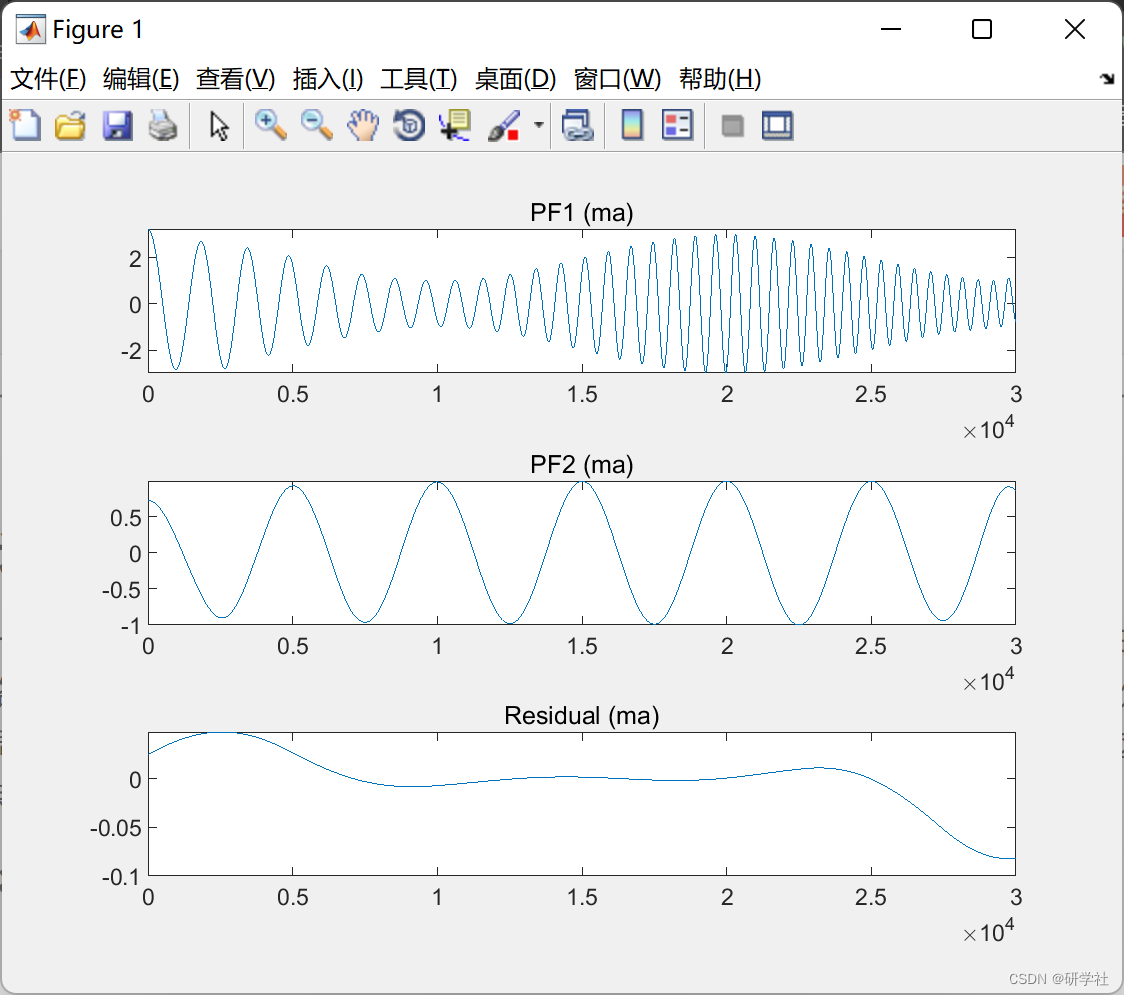
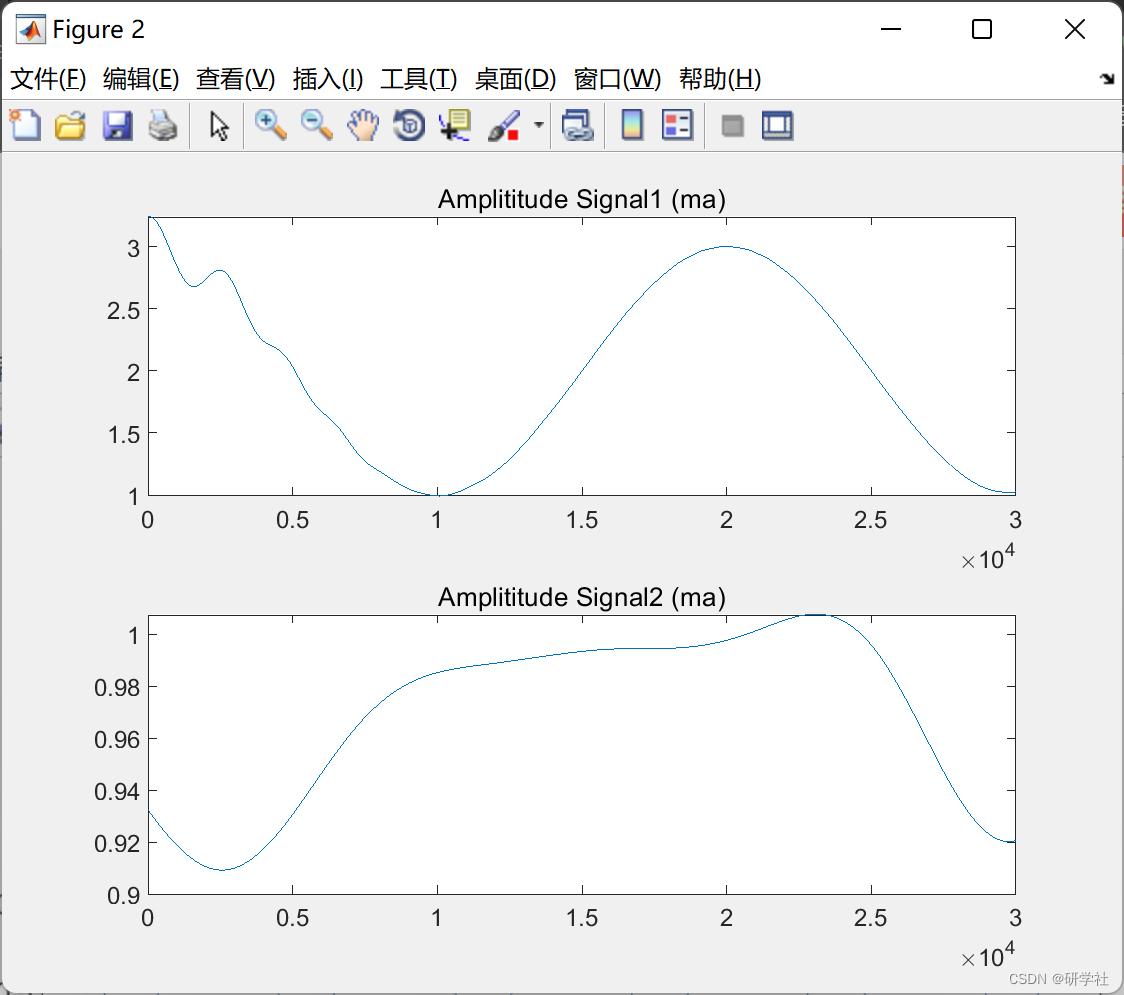
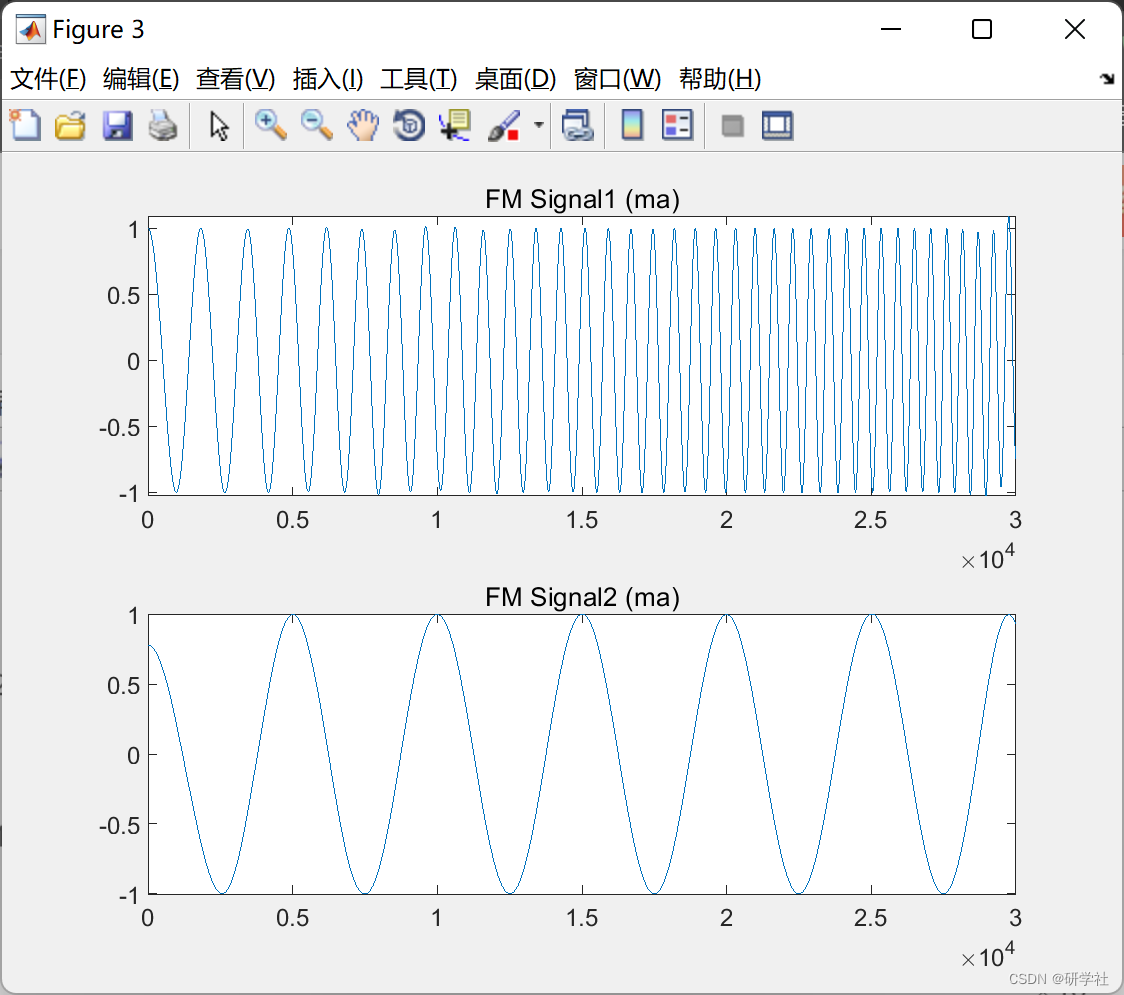
部分代码：

[x, display, stop_thre, sifting_stopping_mode, max_iter, max_pfs, smooth_mode,...
    ma_span, ma_iter_mode, extd_r, x_energy, pfs, ams, fms, iterNum, fvs]...
    = initial(x,varargin{:});

% Initialize main loop
i = 0;
xs = x; % copy x to xs for sifting process, reserve original input as x.
nx = length(x);

while i < max_pfs && ~stoplmd(xs, x_energy) % outer loop for PF selection    
    i = i+1;    
    % initialize variables used in PF sifting loop
    a_i = ones(1,nx);
    s_j = zeros(max_iter,nx);
    a_ij = zeros(max_iter, nx);
    
    % PF sifting iteration loop
    j = 0;
    stop_sifting = 0;
    s = xs;
    
    while j < max_iter && ~stop_sifting %  inner loop for sifting process
        
        j = j+1;
        [m_j, a_j, n_extr] = lmd_mean_amp(s, smooth_mode, ma_span, ma_iter_mode,...
            extd_r);
        % force to stop iter if number of extrema of s is smaller than 3.
        if n_extr < 3
            break;
        end
        h_j = s-m_j; % remove mean.
        s = h_j./a_j; % demodulate amplitude.
        a_i = a_i .* a_j; % mulitiply every ai
        a_ij(j, :) = a_i;
        s_j(j, :) = s;
        [stop_sifting,fvs(i,:)] = is_sifting_stopping(a_j, j, fvs(i,:), sifting_stopping_mode, stop_thre);
        
    end % sift iteration loop
    
    switch sifting_stopping_mode
        case {'liu'}
            [~, opt0] = min(fvs(i,1:j)); % ***Critical Step***
            opt_IterNum = min(j, opt0); % in case iteration stop for n_extr<3
            %             opt_IterNum = min(j-2, opt0);
        otherwise
            error('No specifications for sifting_stopping_mode.');
    end
    
    ams(i, :) = a_ij(opt_IterNum, :); % save each amplitude modulation function in ams.
    fms(i, :) = s_j(opt_IterNum, :); % save each pure frequency modulation function in fms.
    pfs(i, :) = ams(i, :).*fms(i, :); % gain Product Funcion.
    xs = xs-pfs(i, :); % remove PF just obtained from input signal;
    
    iterNum(i) = opt_IterNum; % record the iteration times taken by of each PF sifing.
    
end % main loop

pfs(i+1, :) = xs; % save residual in the last row of PFs matrix.
ams(i+1:end,:) = []; fms(i+1:end,:) = []; pfs(i+2:end,:) = []; fvs(i+1:end,:) = [];
ort = io(x, pfs);

% Output visualization
if display == 1
    lmdplot(pfs, ams, fms, smooth_mode);
end

end

%--------------------------- built-in functions ---------------------------
% initialize signal and options
function [x, display, stop_thre, sifting_stopping_mode, max_iter, max_pfs, smooth_mode,...
    ma_span, ma_iter_mode, extd_r, x_energy, pfs, ams, fms, iterNum, fvs]...
    = initial(x,varargin)

% option fields(i.e. name)
optn_fields = {'display', 'stop_thre', 'sifting_stopping_mode',  'max_iter',...
    'max_pfs', 'smooth_mode', 'ma_span', 'ma_iter_mode','extd_r', 'fix','fix_h'};

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1] 刘志亮， 金亚强， 左明军， 冯志鹏.基于鲁棒局部均值分解的时频表示，用于多分量AM-FM信号分析。机械系统和信号处理。95: 468-487, 2017.
[2] Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454.
[3] G. Rilling, P. Flandrin and P. Goncalves. On empirical mode decomposition and its algorithms. IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing NSIP-03, Grado (I), June 2003

🌈4 Matlab代码实现