🚀 作者:阿辉不一般
🚀 你说呢:生活本来沉闷,但跑起来就有风
🚀 专栏:爱上C语言
🚀作图工具:draw.io(免费开源的作图网站)
如果觉得文章对你有帮助的话,还请点赞,关注,收藏支持博主,如有不足还请指点,博主及时改正,感谢大家支持!!!
文章目录
- 🚀前言
- 🚀算数操作符
- 🚀关系操作符
- 🚀前置++(--)和后置++(--)
- 🚀逻辑操作符
- 🚀条件操作符
- 🚀逗号表达式
- 🚀下标引用操作符
- 🚀函数调用操作符
🚀前言
大家好啊😉!今天阿辉将为大家介绍C语言中的部分操作符,✍包括算数操作符,关系操作符,前置后置++,逻辑操作符,条件操作符,逗号表达式等操作符,剩下的操作符将在下一篇文章中讲解关注阿辉不迷路哦 😘 ,内容干货满满😋,接下来就跟着阿辉一起学习吧👊
🚀算数操作符
算数操作符:
+(加) -(减) *(乘) /(除) %(取模)这几个操作符最为常见
这里我们重点讲一下/(除) %(取模)这两个操作符,另外三个操作符很简单相信大家都掌握了
/除法操作符: 要注意的就是 /的两个操作数都为整数时执行的是整数除法,相除得到的结果也是整数,只有当其中一个操作数为浮点数时执行浮点数除法
🌰栗子
#include<stdio.h>
int main()
{
printf("%d\n", 5 / 2);//整数除法
printf("%f\n", 5.0 / 2);//浮点数除法
return 0;
}

%取模操作符: 取模操作符的两个操作数只能是整数,取模其实就是取余,当被取余数(取模操作符左边的操作数)为负数时,余数也为负数
🌰栗子
#include<stdio.h>
int main()
{
printf("%d\n", 5 % 2);
printf("%d\n", -5 % 2);
return 0;
}

🚀关系操作符
< //判断小于
> //判断大于
<= //判断小于等于
>= //判断大于等于
== //判断等于
!= //判断不等于
关系操作符的返回结果为真 或 假
常用在if 语句、while语句、for语句中
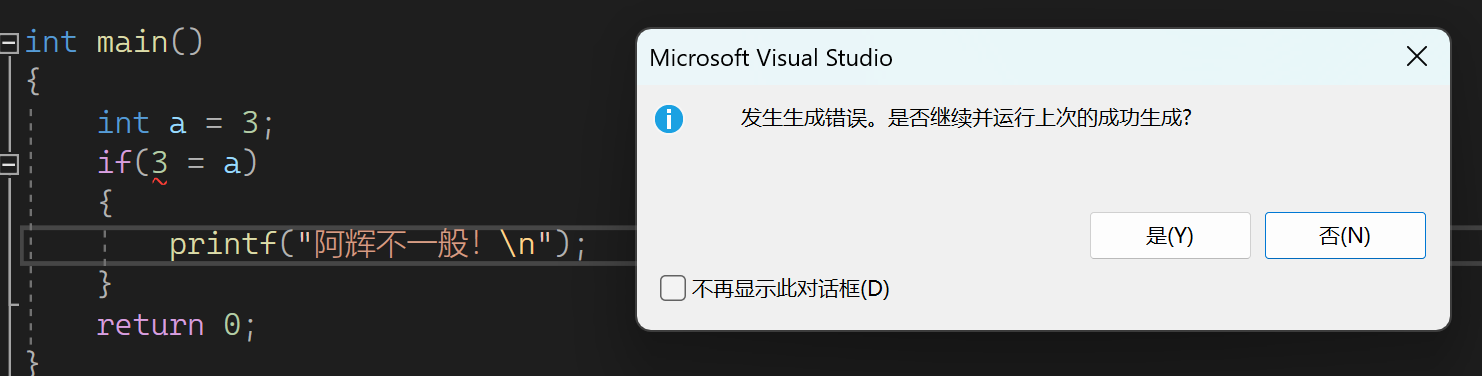
注意: ==很容易写成=,从而造成bug
但是如果你像下面这样写编译器能帮你发现错误 😉
🚀前置++(–)和后置++(–)
前置++(–):操作数先
++(--)自增1(自减1),后使用
后置++(–):操作数使用,后先++(--)自增1(自减1)
🌰栗子
int main()
{
int a = 0;
int b = 0;
if (++a)
printf("阿辉不一般!\n");
if (b++)
printf("阿辉很一般!\n");
printf("a = %d b = %d\n", a, b);
return 0;

我们可以看到仅仅打印了
阿辉不一般!并没有打印阿辉很一般!因为a,b的初始值是0,a是前置++,前置++先自增1后使用,if进行判断的时候a的值为1为真;b是后置++,后置++先使用,后自增1,if进行判断时b的值为0为假;不过前置++和后置++最后都会自增
🚀逻辑操作符
&& 逻辑与
|| 逻辑或
&&逻辑与操作符两边的表达式都为真才为真,否则为假
||逻辑或操作符两边的表达式都为假才为假,否则为真
重点来了👊
我们先看代码
int main()
{
int a = 0;
int b = 0;
int c = 0;
a && ++b;
++c || ++a;
printf("a = %d b = %d c = %d\n", a, b, c);
return 0;
}
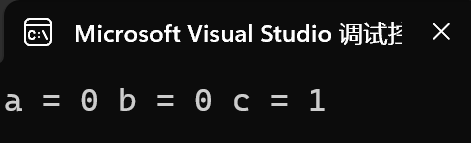
我们发现
a和b的值都为0并没有自增,这是为什么呢?
这是因为&&逻辑与操作符遵循从左至右计算,它的左操作数(也就是前面的一个操作数)为假时整个表达式也就为假了,这时&&并不需要计算右操作数的真假,也就是说这时&&不会去执行后面的表达式,所以++b并没有执行
||逻辑或操作符也遵循从左至右计算,它的左操作数(也就是前面的一个操作数)为真时整个表达式也就为真了,这时||并不需要计算右操作数的真假,也就是说这时||不会去执行后面的表达式,所以++a并没有执行
上述现象也被称为短路现象
这编译器还怪懒嘞 😆
🚀条件操作符
条件操作符 表达式? 语句1: 语句2;也叫三目操作符,当表达式结果为真时,执行语句1,表达式结果为假时,执行语句2.
🌰栗子
#include <stdio.h>
int main()
{
int a = 0;
int b = 0;
scanf("%d%d", &a, &b);
(a > b) ? printf("较大的数是%d\n",a) : printf("较大的数是%d\n", b);
return 0;
}


🚀逗号表达式
逗号表达式的使用方法:
表达式1,表达式2,...,表达式n;
逗号表达式从左向右依次计算,最后一个表达式的结果是整个表达式的结果
🌰栗子
#include <stdio.h>
int main()
{
int x = 0, a = 1, b = 2, c = 3, d = 5;
x = (a++, b + 2, c += 2, a + d);
printf("x=%d\n", x);
printf("a=%d,b=%d,c=%d,d=%d", a, b, c, d);
return 0;
}

因为逗号表达式,从左向右依次执行。整个表达式的结果是最后一个表达式的结果
所以a++会执行使得a+1,
b+2虽然也被执行了,但是并没有重新赋值给b,所以只是进行了简单计算,并没有进行赋值操作,所以b没有变化
c+=2执行后c被重新赋值了,所以c+2
最后:x=a+d=2+5=7
🚀下标引用操作符
这个[]操作符是不是很熟,没错我们在数组那里用来访问数组中各个元素用到的操作符,死去的记忆突然攻击我 😵
使用方法:
数组名[ 操作数 ]
详细讲解可以看看阿辉之前的文章 数组篇
🚀函数调用操作符
函数调用操作符()可以有多个操作数,但至少有一个操作数——函数名
函数名(变量1,变量2,...,变量n);
🌰栗子
int add(int a, int b)
{
return a + b;
}
int main()
{
int a = 2;
int b = 3;
int sum = add(a, b);
printf("%d\n", sum)l;
return 0;
}
到这里,阿辉今天对于C语言操作符的分享就结束了,希望这篇博客能让大家有所收获, 如果觉得阿辉写得不错的话,记得给个赞呗,你们的支持是我创作的最大动力🌹