- 感觉这三种方法有联系,RBF用多个加权高斯拟合值函数,GMM用多个加权高斯拟合联合分布函数,GMM的加权相比于概率更像FUZZY里的隶属度,并且FUZZY的不同规则实现的就是一定程度的聚类。
一、RBF
资料:https://blog.csdn.net/weixin_40802676/article/details/100805545
1、模型描述
- 总共分为三层,第一层是输入层,第二层隐藏层,第三层是全连接层。
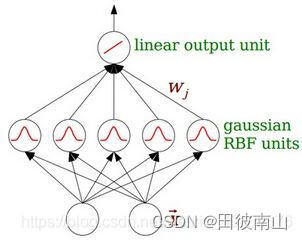
- 隐藏层是多元高斯分布概率密度函数,将输入层所有变量输入,输出一个待加权项。隐藏层的个数是很重要的参数,每个高斯分布的参数是不同的。
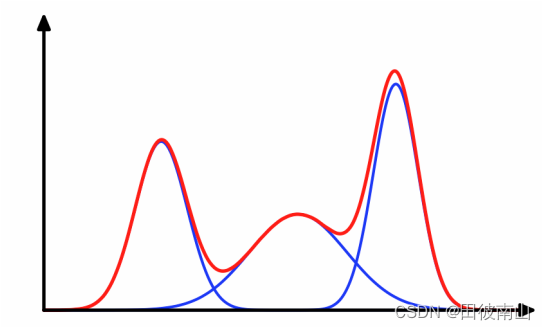
- 径向基神经网络可以看作是若干个多元高斯分布的加权和。
2、参数优化
(1)中心向量和宽度
中心向量(均值)
- 中心向量刚开始可以随机选取,之后在随机选取的基础上进行优化
K-均值聚类

宽度(方差)
- 方差代表的是数据的“扩散/集中程度”,数值越大,分布越扩散。也就说方差越大,单个分布对其他分布的影响就越大。所以这个方差值要有所有中心点之间的关系去计算

(2)权重和偏置
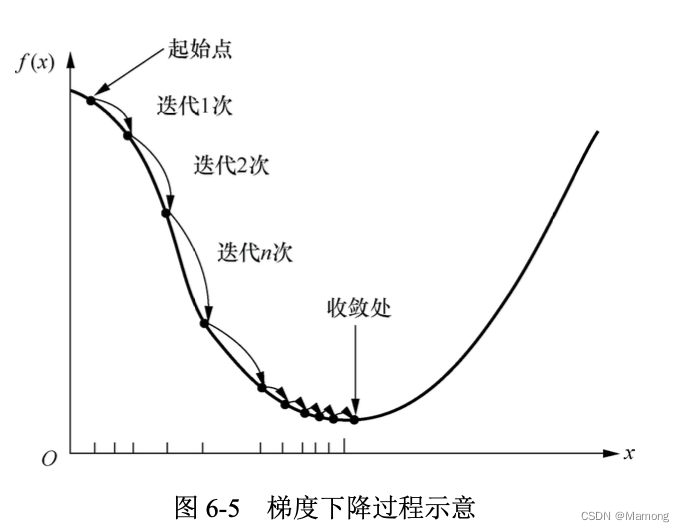
- 如果中心向量和宽度已知,则输出层就是一个单层的全连接,只要梯度下降即可进行优化
- 单层的问题也可以使用最小二乘法(这二者在这种情况下,如何区分优劣呢?)
二、GMM
1、模型描述
- GMM本身也是多个高斯分布的加权和,但是它想逼近的是一个联合分布函数。注意这里和径向基神经网络的区别,高斯混合分布的空间是 输入×输出 ,是无监督的聚类。而径向基神经网络则是一种回归算法,是在拟合目标函数。
2、参数优化
(1)最大似然估计
- 如果已知一组数据符合一个正态分布,但不知道正态分布的参数,可以通过最大似然函数去估计均值和方差。

- 当对似然函数做最大化处理,当似然函数最大时,此时的参数就是“最有可能”的参数
(2)EM算法
资料:https://zhuanlan.zhihu.com/p/326055752
(3)EM算法在GMM上的应用
资料:https://zhuanlan.zhihu.com/p/30483076

3、GMR
-
利用GMM训练的函数作为联合分布函数
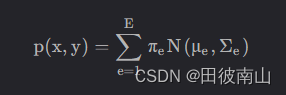
-
通过联合分布函数计算条件概率P(输出|输入)
证明过程资料:https://www.zhihu.com/tardis/zm/art/74068143?source_id=1005
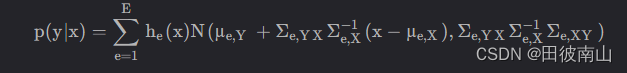
-
通过条件概率计算期望作为对输出的估计
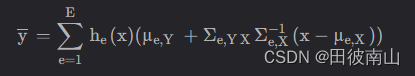
三、FUZZY
资料:https://blog.csdn.net/qq_40943760/article/details/122261531
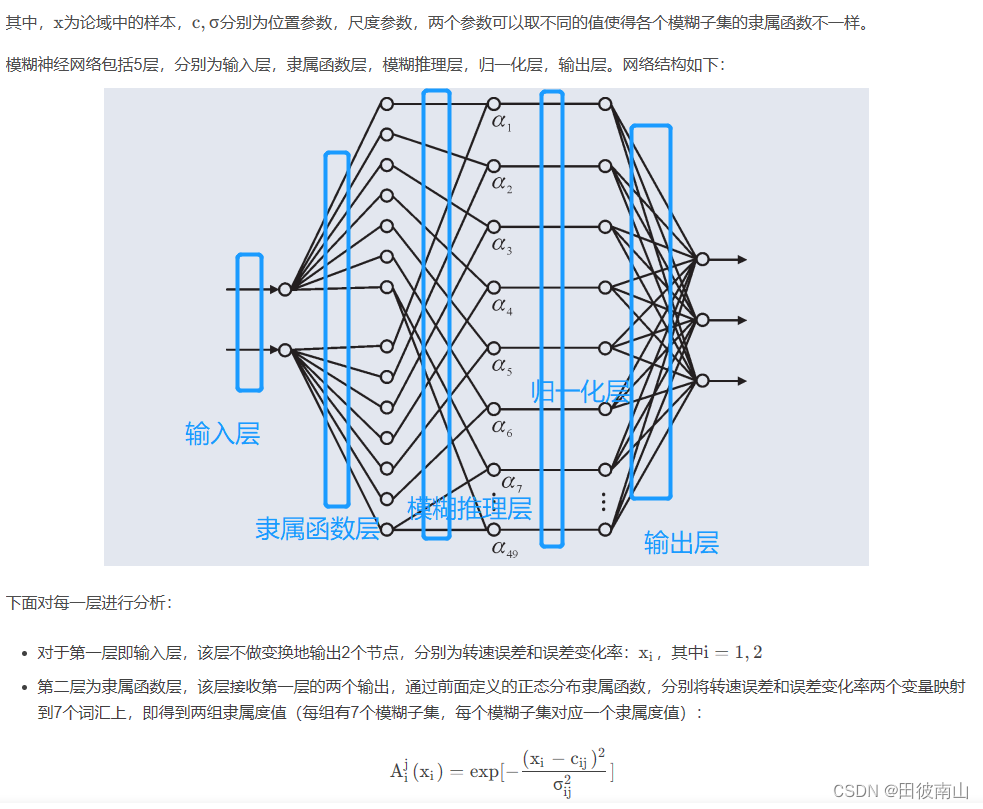
模糊神经网络