优化问题可以分为凸优化问题和非凸优化问题,凸优化问题是指定义在凸集中的凸函数最优化的问题,典型应用场景就是 目标函数极值问题的求解。凸优化问题的局部最优解就是全局最优解,因此 机器学习中很多非凸优化问题都需要被转化为等价凸优化问题或者被近似为凸优化问题。
6.1 通俗讲解凸函数
6.1.1 什么是凸集
凸集表示一个欧几里得空间中的区域,这个区域具有如下特点:区域内任意两点之间的线段都包含在该区域内;更为数学化的表述为,集合 C 内任意两点间的线段也均在集合 C 内,则 称集合 C 为凸集。
6.1.2 什么是凸函数
凸函数是一个定义在某个向量空间的凸子集 C(区间)上的实值函数 f,而且对于凸子集 C 中的任意两个向量,如果 f((x1+x2)/2) ≤ (f(x1)+f(x2))/2,则 f(x) 是定义在凸子集 C 中的凸函数。实 际上,如果某函数的上镜图(函数曲线上的点和函数曲线上方所有的点的集合)是凸集,那么 该函数就是凸函数。
6.1.3 机器学习“热爱”凸函数
凸函数的局部极小值就是全局最小值。机器学习中有很多优化问题都要通过凸优化来 求解,另外一些非凸优化问题也常常被转化为凸优化问题来求解。学术界对于非凸优化的优化问题也没有一个很好的通用解决方法。
6.2 通俗讲解梯度下降
梯度下降法是一种逐步迭代、逐步缩减损失函数值,从而使损失函数值最小的方法。
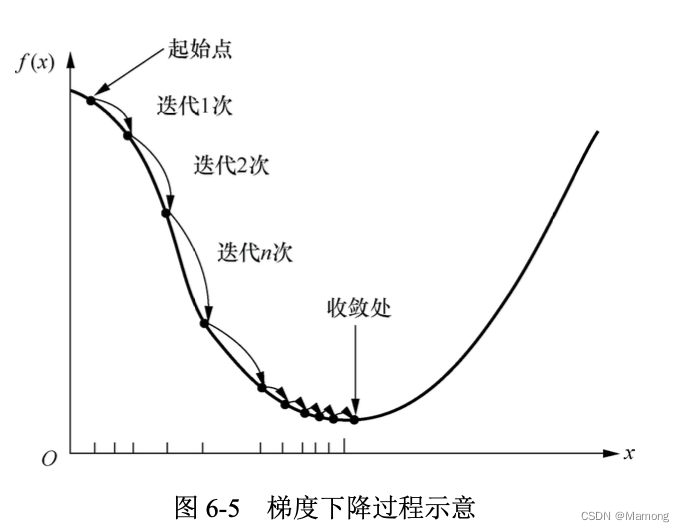
首先,选取任意参数(ω 和 b)值作为起始值。
其次,明确迭代方向,逐步迭代。这个最陡在数学上的表现就是梯度,也就是说沿着负梯度方向下降能够最快到达山谷。
最后,确定迭代步长。当我们沿着负梯度方向进行迭代的时 候“每次走多大的距离”,也就是“学习率”的大小是需要算法工程师去调试的;或者说,算法 工程师的一项工作就是要调试合适的“学习率”,从而找到“最佳”参数。
6.2.1 梯度是什么
一般来说,梯度可以定义为一个函数的全部偏导数构成的向量。总结来说有如下两种情况。
(1)在单变量函数中,梯度就是函数的导数,表示函数在某个给定点的切线斜率,表示单位自变量变化引起的因变量变化值。
(2)在多变量函数中,梯度就是函数分别对每个变量进行微分的结果,表示函数在给定点上升最快的方向和单位自变量(每个自变量)变化引起的因变量变化值。
梯度是一个向量,它的方向就是函数在给定点上升最快的方向,因此负梯度方向就是函数 在给定点下降最快的方向。一旦我们知道了梯度,就相当于知道了凸函数下降最快的方向。
6.2.2 梯度下降与参数求解
梯度下降是一种求解凸函数极值的方法,它以损失函数作为纽带,从而在机器学习的参数 求解过程中“大放异彩”。损失函数是模型预测值与训练集数据真实值的差距,它是模型参数 (如 ω 和 b)的函数。
损失函数描述的是个体预测值与真实值的差距,成本函数描述的是总体预测值与真实 值的差距,但由于两者本质上一致且只在引入样本数据进行模型实际求解的时候才需要严格区分,因此大部分图书中并未严格区分两者,往往都是用损失函数来统一指代。