做题的时候看到了单调栈,但是不知道是个什么玩意,记录一下吧。
单调栈含义
单调栈是一种特殊的数据结构,用于解决一些与单调性相关的问题。它的基本含义是在栈的基础上,维护一个单调递增或单调递减的栈。
在单调递增栈中,栈内元素从栈底到栈顶是递增有序的,而在单调递减栈中,栈内元素从栈底到栈顶是递减有序的。
单调栈的基本使用是通过维护栈内元素的单调性,来解决一些与单调性相关的问题。常见的应用场景包括:
- 下一个更大元素:给定一个数组,对于每个元素,找到它右边第一个比它大的元素。
- 下一个更小元素:给定一个数组,对于每个元素,找到它右边第一个比它小的元素。
- 最大矩形面积:给定一个二维矩阵,求其中全为1的最大矩形的面积。
使用单调栈解决这些问题的基本思路是,遍历数组或矩阵中的元素,将元素依次入栈,并在入栈时维护栈内元素的单调性。当遇到一个元素破坏了栈内元素的单调性时,可以根据问题的要求进行相应的处理,然后将该元素入栈。
通过这种方式,可以在O(n)的时间复杂度内解决一些与单调性相关的问题,其中n是数组或矩阵的大小。
看到个题目,昨天,想自己用单调栈做出来,但是没做出来,上网看了下有一些解法,但是都存在问题?然后叫ChatGPT写了一个,感觉能用,也测试了一下,确实可以,但是为什么可以这样做,还是有点懵,既然不懂那就死记硬背吧。
视野总和
描叙:有n个人站队,所有的人全部向右看,个子高的可以看到个子低的发型,给出每个人的身高,问所有人能看到其他人发现总和是多少。
输入:4 3 7 1
输出:2解释:个子为4的可以看到个子为3的发型,个子为7可以看到个子为1的身高,所以1+1=2
思路:观察题之后,我们发现实际上题目转化为找当前数字向右查找的第一个大于他的数字之间有多少个数字,然后将每个结果累计就是答案。
public static int calculateFieldSum(int[] heights) {
int n = heights.length;
Stack<Integer> stack = new Stack<>();
int sum = 0;
for (int i = 0; i < n; i++) {
while (!stack.isEmpty() && heights[i] >= heights[stack.peek()]) {
stack.pop();
}
sum += stack.size();
stack.push(i);
}
return sum;
}柱状图中最大的矩形
这一题,自己先用普通的栈去实现,但是发现只能解决部分问题,存在局限性(也有可能是能力不足哈哈不会写)然后看了答案以后可以使用单调栈来实现。这一题的思路其实很简单,但是如果暴力的话肯定会超时的而且比较麻烦,所以可以用单调栈来解决,设计一个单调递增栈来解决问题,一旦出现有元素小于栈顶,则开始计算目前的矩形最大面积是多少。不过这一题里面加了两个零边界值,目前刚学,没有发现这两个零的特殊作用,查阅资料后才恍然大悟:
在这个算法中,将原始数组 heights 的长度加2,并在新数组 m 的开头和末尾分别设置为0,是为了处理边界情况。
在解决最大矩形面积问题时,需要考虑到矩形的边界情况。通过在 m 数组的开头和末尾添加高度为0的元素,可以确保栈中的元素都能找到对应的左边界和右边界。
具体来说,在遍历 m 数组时,当遇到一个元素小于栈顶元素时,表示栈顶元素的右边界确定,可以计算以栈顶元素为高度的矩形的面积。如果没有添加开头和末尾的0元素,那么在某些情况下,栈中的元素可能无法找到对应的左边界或右边界,导致计算面积时出现错误。
因此,通过在 m 数组的开头和末尾添加高度为0的元素,可以确保栈中的元素都能找到对应的左边界和右边界,从而正确计算最大矩形面积。
比如说:2 1 5 6 2 3 这个数据
我们如果不设置两个0的话,那么我们数据遍历完后,栈中其实还是有数据的。如果栈中的数据是最大值的话,因为我们最后设置了个0,又因为本题数据0 <= heights[i] <= 10000,所以最后一次计算的时候,也会把剩余的栈中元素再计算他们的最大矩形值。
题目如下:
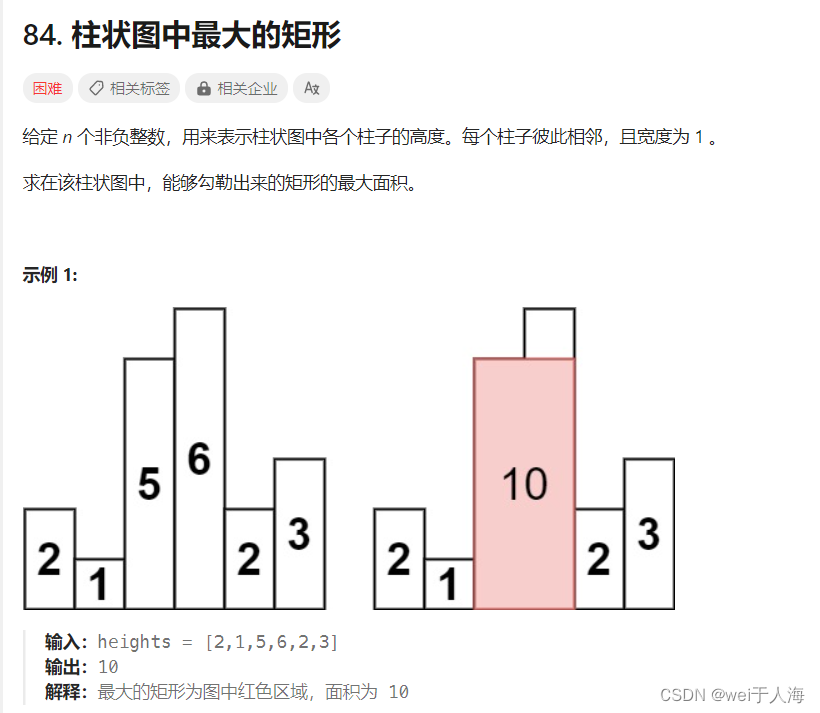
代码如下,开袋即食:
class Solution {
public int largestRectangleArea(int[] heights) {
if(heights.length==1) return heights[0];
int res = 0;
Stack<Integer> s = new Stack<>();
int[] newH = new int[heights.length+2];
newH[0] = 0;
newH[heights.length+1]=0;
for(int i = 1 ; i<heights.length+1;i++){
newH[i] = heights[i-1];
}
for(int i = 0;i<newH.length;i++){
while(!s.isEmpty()&&newH[i]<newH[s.peek()]){
int p = s.pop();
int h = newH[p];
int leftIndex = s.peek();
int w = i-leftIndex-1;
res = Math.max(res,h*w);
}
s.push(i);
}
return res;
}
}