问题描述

给定一个有n（n≥1）个整数的序列，要求求出其中最大连续子序列的和。
在这里插入图片描述

蛮力法

暴力枚举

/**
 * 时间复杂度：O(n^3)
 * @param arr 序列[数组]
 * @param n 数组大小
 * @return int 
 */
int maxSubSum1(int arr[], int n) {
    int thisSum; // 子序列的和
    int maxSum = arr[0]; // 最大连续子序列的和
    for(int i = 0;i < n;i++) {
        for(int j = i;j < n;j++) { // 两重循环穷举所有的连续子序列
            // 计算子序列的和
            thisSum = 0;
            for(int k = i;k <= j;k++) {
                thisSum += arr[k];
            }
            // 通过比较求最大子序列的和
            if(thisSum > maxSum) {
                maxSum = thisSum;
            }
        }
    }
    return maxSum;
}

优化枚举法

暴力枚举存在的问题：
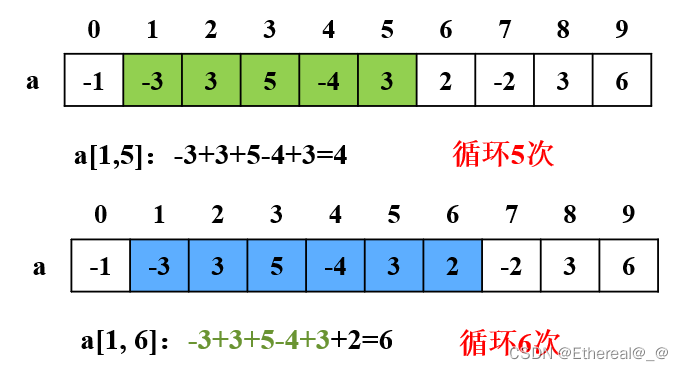
在这里插入图片描述
使用暴力枚举的时候存在重复计算的情况，可以改进来减少重复计算。
a[1,6] = a[1,5] + a[6]

在这里插入图片描述

// 优化枚举法  时间复杂度：O(n^2)
int maxSubSum2(int arr[], int n) {
    int thisSum; // 子序列的和
    int maxSum = arr[0]; // 最大连续子序列的和
    for(int i = 0;i < n;i++) {
        thisSum = 0;
        for(int j = i;j < n;j++) {
            thisSum+=arr[j];
            if(thisSum > maxSum) {
                maxSum = thisSum;
            }
        }
    }
    return maxSum;
}

改进的优化枚举法

对于 maxSubSum2() 算法，还可以进一步改进。

在扫描序列的时候，如果扫描中遇到负数，当前子序列和 thisSum 将会减小，若 thisSum 为负数，表明前面已经扫描的那个子序列可以抛弃了，则放弃这个子序列，重新开始下一个子序列的分析，并置 thisSum 为0。
若这个子序列和 thisSum 不断增加，那么最大子序列和 maxSum 也会不断增加。

// 改进的优化枚举法  时间复杂度：O(n)
int maxSubSum3(int arr[], int n) {
    int thisSum = 0; // 子序列的和
    int maxSum = arr[0]; // 最大连续子序列的和
    for(int i = 0;i < n;i++) {
        thisSum += arr[i];
        // 若当前子序列的和为负数，就重新开始下一子序列
        if(thisSum < 0) {
            thisSum = 0;
        }
        // 比较求最大连续子序列
        if(thisSum > maxSum) {
            maxSum = thisSum;
        }
    }
    return maxSum;
}

分治法

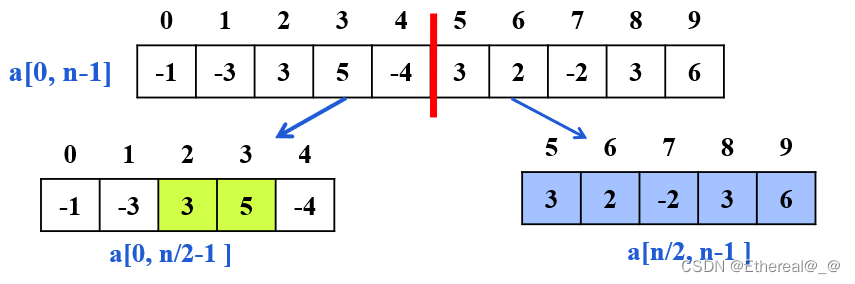
在这里插入图片描述

将数组 a[0,n-1] 分解为 a[0, n/2-1 ] 和 a[n/2, n-1 ]；
递归求解子问题：左半部分的最大连续子序列和A1=8，右半部分的最大连续子序列和A2=12
合并子问题，得到原问题的最大子序列和。若跨中点的最大连续子序列和A3；则原序列的最大连续子序列和为max{A1,A2,A3}

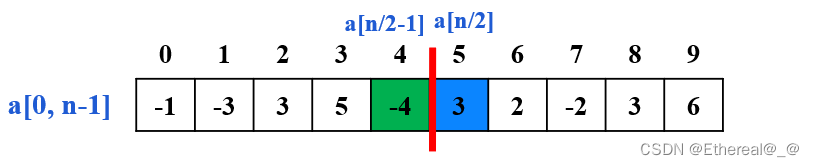
求解跨中点的最大子序列的和：

记 mid = n/2 - 1
则A3可以分成两个部分：left + right
left：以 a[mid] 为结尾的最大连续子序列的和；right：以 a[mid+1] 为开端的最大连续子序列的和
分别求出 left 和 right 即可得到 A3

int getMax(int a, int b, int c) {
    int temp = a > b ? a : b;
    int max = temp > c ? temp : c;
    return max;
}


// 分治法  时间复杂度：O(nlogn)
// left--数组起始下标，right--数组结束下标
int maxSubSum4(int arr[], int left, int right) {
    // 子序列只有一个元素时
    if(left == right) {
        if(arr[left] > 0) return arr[left];
        else return 0;
    }

    int maxLeftSum = 0, maxRightSum = 0;
    int maxLeftBorderSum = 0, leftBorderSum = 0;
    int maxRightBorderSum = 0, rightBorderSum = 0;
    
    int mid = (left + right)/2;

    maxLeftSum = maxSubSum4(arr, left, mid);
    maxRightSum = maxSubSum4(arr, mid+1, right);
	// 求出以左边加上a[mid]元素构成的序列的最大和
    for(int i = mid;i >= left;i--) {
        leftBorderSum += arr[i];
        if(leftBorderSum > maxLeftBorderSum) {
            maxLeftBorderSum = leftBorderSum;
        }
    }
	// 求出a[mid]右边元素构成的序列的最大和
    for(int j = mid+1;j <= right;j++) {
        rightBorderSum += arr[j];
        if(rightBorderSum > maxRightBorderSum) {
            maxRightBorderSum = rightBorderSum;
        }
    }
    return getMax(maxLeftSum, maxRightSum, maxLeftBorderSum+maxRightBorderSum);
}

动态规划

在这里插入图片描述
可以得到 dp[j] 的递推方程：

则序列a的最大连续子序列和等于dp[j]（1≤j≤n）中的最大者。

// 动态规划  时间复杂度：O(n)
// 对于含有n个整数的序列a,设dp[j]表示以a[j]结尾的最大连续子序列和
int maxSubSum5(int arr[], int n) {
    int dp[n];
    dp[0] = arr[0];
    for(int i = 1;i < n;i++) {
        if(dp[i-1] > 0) {
            dp[i] = dp[i-1] + arr[i];
        } else {
            dp[i] = arr[i];
        }
    }
    // 查找dp[]数组中的最大者
    int maxSum = dp[0];
    for(int j = 0;j < n;j++) {
        if(dp[j] > maxSum) {
            maxSum = dp[j];
        }
    }
    return maxSum;
}