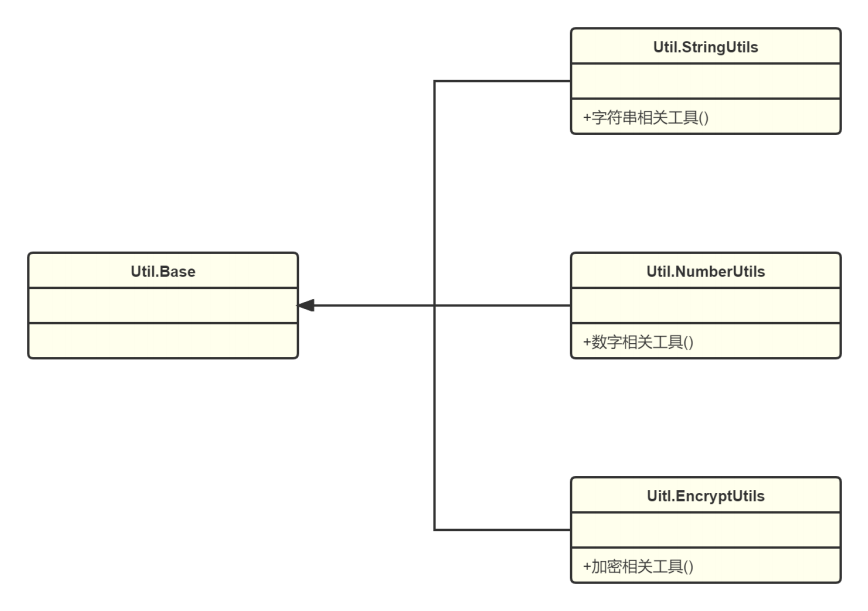
线性回归是有监督学习中的经典问题，其核心在于找到样本的多个特征与标签值之间的线性关系。样本集中的第j个样本可被表示为：

特征向量： $X_j=\begin{bmatrix} x_{j1} &x_{j2} & \hdots & x_{jn} \end{bmatrix}$
标签值： $u_j$

而线性回归系统给出权重向量：

$w=\begin{bmatrix} w_0 & w_1 & w_2 & \hdots & w_n \end{bmatrix}^T$

使得该样本的预测值为：

$y_j=w_0+X_jw=w_0+\sum^n_{i=1}x_{ji}w_i$

当所有样本的预测值与标签值的误差最小时，即代表该线性回归系统找到了最优的拟合曲线

本文采用了梯度下降法以解决线性回归问题。梯度下降法与现代控制系统相似，现代控制系统实现的梯度下降法如下：

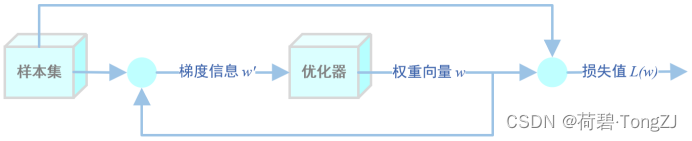
该系统将线性回归问题的权重向量 $w$ 作为状态变量，以损失函数 $L(w)$ 反向传播的梯度 $-\frac{dL(w)}{dw}$ 作为 $\frac{dw}{dt}$ ，并通过 $w= w +\frac{dw}{dt} dt$ 对权重向量进行更新(其中的 $dt$ 可视为学习率)，使得所有样本的误差越来越小

状态空间描述

在前文的讨论中，样本的预测值表示为“特征向量×权重向量+偏置”的形式。为了后续计算的整洁，将样本的特征向量表示为:

$X_j=\begin{bmatrix} 1 & x_{j1} &x_{j2} & \hdots & x_{jn} \end{bmatrix}$

则样本的预测值可被重写为：

$y_j=X_jw$

以样本的预测值与标签值的差值作为误差 $e$ ：

$e=y-u=\begin{bmatrix} 1& x_{11} & x_{12} & \hdots & x_{1n}\\ 1& x_{21}&x_{22} & \hdots & x_{2n}\\ \vdots &\vdots &\vdots & \ddots &\vdots \\ 1& x_{m1}& x_{m2}& \hdots & x_{mn}\end{bmatrix} w - \begin{bmatrix} u_1\\ u_2\\ \hdots\\ u_m \end{bmatrix}$

误差e的值域为 $(- \infty, \infty)$ ，最优值为 0，显然不可直接作为梯度下降法的损失函数。故以其原函数 (MSE) 作为损失函数：

$L(w)=\frac{\overline{e^2}}{2} \in [0, \infty)$

$\frac{\partial L(w)}{\partial w_i}=\overline{(e\frac{\partial e}{\partial w_i})} = \overline{(x_{.i}X)}w - \overline{(x_{.i}u)},\ x_{.0}=1$

$\frac{dL(w)}{dw}=\begin{bmatrix} 1 & \overline{x_{.1}} & \overline{x_{.2}} & \hdots&\overline{x_{.n}} \\ \overline{x_{.1}} & \overline{x_{.1}^2} & \overline{x_{.1}x_{.2}} & \hdots & \overline{x_{.1}x_{.n}}\\ \vdots &\vdots & \vdots &\ddots &\vdots \\ \overline{x_{.n}} & \overline{x_{.n}x_{.1}} & \overline{x_{.n}x_{.2}} & \hdots & \overline{x_{.n}^2} \end{bmatrix} w - \begin{bmatrix} \overline{u}\\ \overline{(x_{.1}u)}\\ \vdots\\ \overline{(x_{.n}u)} \end{bmatrix}$

由梯度下降法可知，以 $w = w - \frac{dL(w)}{dw} p$ 的方式对权重向量进行更新，将使得损失函数 $L(w)$ 逐渐减小。故令 $\frac{dw}{dt}=-\frac{dL(w)}{dw},\ dt=p$ ，以 $w=w+\frac{dw}{dt}dt$ 对权重向量进行更新。综上所述，该系统的状态空间描述为：

状态方程： $\dot{w}=-\begin{bmatrix} 1 & \overline{x_{.1}} & \overline{x_{.2}} & \hdots&\overline{x_{.n}} \\ \overline{x_{.1}} & \overline{x_{.1}^2} & \overline{x_{.1}x_{.2}} & \hdots & \overline{x_{.1}x_{.n}}\\ \vdots &\vdots & \vdots &\ddots &\vdots \\ \overline{x_{.n}} & \overline{x_{.n}x_{.1}} & \overline{x_{.n}x_{.2}} & \hdots & \overline{x_{.n}^2} \end{bmatrix} w + \begin{bmatrix} \overline{u}\\ \overline{(x_{.1}u)}\\ \vdots\\ \overline{(x_{.n}u)} \end{bmatrix} 1(t)$
输出方程： $e=\begin{bmatrix} 1& x_{11} & x_{12} & \hdots & x_{1n}\\ 1& x_{21}&x_{22} & \hdots & x_{2n}\\ \vdots &\vdots &\vdots & \ddots &\vdots \\ 1& x_{m1}& x_{m2}& \hdots & x_{mn}\end{bmatrix} w - \begin{bmatrix} u_1\\ u_2\\ \hdots\\ u_m \end{bmatrix} 1(t)$

其中，状态方程描述了权重向量 $w$ 随时间变化的速度，输出方程描述了该线性回归系统对每一个样本的误差

实验案例

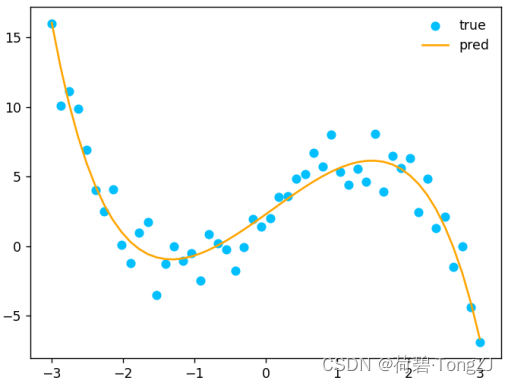
给定定义域 $x \in [-3, 3]$ ，在下式所示的曲线上均匀地选取样本点 (上图中蓝色散点)，并在纵坐标 (标签值) 上添加噪声：

$y=2+x+0.3x^2-0.5x^3+4\sin{x}$

横坐标为 $x_j$ 的样本的特征向量被定义为：

$X_j = \begin{bmatrix} 1 &x_j & e^{-x_j} & e^{x_j} \end{bmatrix}$

将样本的特征向量与标签值输入线性回归系统，该系统将用曲线 $y=w_0 + w_1x +w_2 e^{-x} + w_3 e^x$ 对样本进行拟合。运行Python程序（见附录)后，还得到状态空间表达式中的四个矩阵

最终拟合曲线为上图中的橙色曲线，该拟合曲线的权重向量为：

$w=\begin{bmatrix} 2.02 & 6.86 & 1.73 & -1.46 \end{bmatrix}^T$

该拟合曲线的方程为：

$y=2.02 + 6.86 x +1.73 e^{-x} - 1.46 e^x$

代码实现

上述系统主要通过 Auto_Ctrl_System 类实现，该类的实例属性有：

A, B, C, D：系统矩阵 A，输入矩阵 B，输出矩阵 C，直接传递矩阵 D
w：权重向量
dstate, output：状态方程、输出方程的结果

实例方法有：

adjust：根据状态方程，调整权重向量
predict：利用当前的权重向量，对样本 (可另给定) 给出预测值
ns_tran：系统非奇异变换，给定转换矩阵 $T$ 使得 $\hat{w}=Tw$ ，对系统的矩阵 A, B, C 进行原地更新
ctrl_2：转换系统为能控标准Ⅱ型， $T=\begin{bmatrix} B & AB & \hdots & A^{n-1}B \end{bmatrix}$
jordan：转换系统为 Jordan 标准型 (该系统中的矩阵 A 为对称矩阵，可对角化)， $T$ 由矩阵 A 的特征向量构成
state_tran：利用矩阵 A 可被对角化这一点，对该系统的状态转移矩阵进行求解

import numpy as np
import sympy as sp
from tqdm import trange

np.set_printoptions(precision=3, suppress=True)
INFO = lambda *args: print(*args, sep='\n')


def simplify(x, eps=1e-5):
    ''' 针对 exp 多项式的简化函数, 不一定普适'''
    if isinstance(x, sp.Add):
        x = list(x.args)
        for i in range(len(x)):
            coef, exp = x[i].args
            coef, exp = map(float, [coef, exp.args[0].args[0]])
            # exp 系数小于阈值, exp 指数项为负数
            if abs(coef) < eps and exp < 0: x[i] = 0
        x = sum(x)
    return x


class Auto_Ctrl_System:
    n = property(fget=lambda self: self.w.size)
    # 状态方程, 输出方程
    dstate = property(fget=lambda self: self.A @ self.w + self.B)
    output = property(fget=lambda self: self.C @ self.w + self.D)
    # 对输入的矩阵预处理 (添加偏置)
    _process = lambda self, x: np.concatenate([np.ones([x.shape[0], 1]), x], axis=1) if self.bias else x

    def __init__(self, x, y, bias=True):
        x, y = map(lambda i: np.float16(i), [x, y])
        n = x.shape[1] + bias
        self.bias = bias
        # 输出方程的矩阵 C, D
        self.C = self._process(x)
        self.D = - y[:, None]
        # 状态方程的矩阵 A, B
        self.A = - (self.C[..., None] * self.C[:, None]).mean(axis=0)
        self.B = - (self.C * self.D).mean(axis=0, keepdims=True).T
        # 初始化权重向量
        self.w = np.random.random([n, 1])

    def adjust(self, epochs=2e4, dt=1e-3):
        qbar = trange(round(epochs))
        for _ in qbar:
            loss = np.square(self.output).mean()
            qbar.set_description(f'MSE {loss:.2f}')
            self.w += self.dstate * dt

    def predict(self, x=None):
        x = self._process(x) if isinstance(x, np.ndarray) else self.C
        return (x @ self.w).flatten()

    def ns_tran(self, tran):
        tran_inv = np.linalg.inv(tran)
        assert np.all(np.isfinite(tran_inv))
        INFO('非奇异变换矩阵:', tran)
        self.A = tran_inv @ self.A @ tran
        self.B = tran_inv @ self.B
        self.C = self.C @ tran

    def ctrl_2(self):
        tran = [self.B]
        for i in range(self.n - 1): tran.append(self.A @ tran[-1])
        tran = np.concatenate(tran, axis=1)
        # 不能控的状态数
        print(f'不能控状态数: {self.n - sp.Matrix(tran).T.rank()}')
        self.ns_tran(tran)
        INFO('能控标准Ⅱ型:', self)

    def jordan(self):
        tran = np.linalg.eig(self.A)[1]
        self.ns_tran(tran)
        INFO('Jordan 标准型:', self)

    def state_tran(self, response=False):
        t = sp.symbols('t')
        # 对角化的变换矩阵
        tran = np.linalg.eig(self.A)[1]
        tran_inv = np.linalg.inv(tran)
        assert np.all(np.isfinite(tran_inv))
        # 状态转移矩阵
        diag = sp.Matrix(np.eye(self.n) * (tran_inv @ self.A @ tran) * t).exp()
        state_tran = tran @ diag @ tran_inv
        # 对 exp 多项式进行简化
        for i in range(self.n):
            for j in range(self.n):
                state_tran[i, j] = simplify(state_tran[i, j])
        INFO('状态转移矩阵:', np.array(state_tran))
        # fixme: 阶跃响应 (针对性求解, 勿用, 需根据状态转移矩阵设计)
        if response:
            fc, f, gc, g, a, b = sp.symbols('f_c, f, g_c, g, a, b')
            # 利用新变量替代状态转移矩阵中的 exp 多项式
            state_tran = sp.Matrix([[fc, 0, f, f],
                                    [0, gc, -g, g],
                                    [f, -g, a + b, a - b],
                                    [f, g, a - b, a + b]])
            # 零输入响应, 零状态响应
            zero_input = state_tran @ self.w
            zero_state = np.linalg.inv(self.A) @ (state_tran - sp.eye(self.n)) @ self.B
            return zero_input, zero_state
        return state_tran

    def __str__(self):
        return str(np.concatenate([self.A, self.B], axis=1))

    __repr__ = __str__


if __name__ == '__main__':
    import matplotlib.pyplot as plt

    x = np.linspace(-3, 3, 50)
    z = np.stack([x, np.exp(-x), np.exp(x)], axis=1)

    np.random.seed(10)
    # 原函数: x + 0.3 x^2 - 0.5 x^3 + 4 sin(x) + 噪声
    y = 2 + x + 0.3 * np.power(x, 2) - 0.5 * np.power(x, 3) + 4 * np.sin(x) + 5 * (np.random.random(len(x)) - 0.5)
    plt.scatter(x, y, c='deepskyblue', label='true')

    acs = Auto_Ctrl_System(z, y, bias=True)
    # 转化为 Jordan 标准型
    acs.jordan()
    acs.adjust(2e4)

    plt.plot(x, acs.predict(), c='orange', label='pred')
    plt.legend(frameon=False)
    plt.show()