论文阅读笔记及代码整理
《Extracting cyclo-stationarity of repetitive transients from envelope
spectrum based on prior-unknown blind deconvolution technique》
代码有优化整理过，需要请下载：https://mbd.pub/o/bread/ZZaTl5ht

贡献：
1.文提出一种基于包络谱定义准则的盲反卷积（BD）技术。
2.所提出的方法不需要任何先验参数，并且对脉冲噪声具有鲁棒性。
3.所提方法优于传统的时域BD方法，包括MED和SF-SLSN
摘要：
传统盲反卷积方法的目标是从时域恢复脉冲信号。针对重复瞬态的循环平稳性，提出了一种新的盲反卷积（BD）技术，就是未知先验的盲反卷积技术，用于提取重复瞬态信号的循环平稳性。该方法通过最小化基于包络谱(ES)定义的最优准则来寻找反滤波器。此外，该方法不需要初始化BD的先验知识。基于该方法和广义Lp/Lq范数，介绍了如何设计一种提取重复瞬态循环平稳性（cyclo-stationarity）的BD算法。（主题就是通过使用ES定义的最优准则提供了一个反卷积的算法框架）

说明
盲反卷积（BD）旨在构建一个逆滤波器，BD得到的逆滤波器抵消了各种外部信号传输路径的影响。
根据不同的优化准则，盲反卷积包括最小熵反卷积(MED)[12]、广义MED[13]、最优最小熵反卷积(OMED)、单层单节点结构稀疏滤波(SF-SLSN)[15]、最大相关峭度反卷积(MCKD)、多点最佳最小熵解卷积调整卷积 (MOMEDA)[17]和基于循环平稳的盲反卷积(CYCBD)应用与脉冲特征检测。
MED的原理是利用峰度最大化的策略来实现逆滤波器
广义MED是通过最大化去卷积信号的 Gary 可变范数来恢复脉冲特征。
OMED使用最大化D范数的策略来获得逆滤波器。
然而，峰度、Gary 变模和 D 模对异常值极为敏感，因此往往会过度突出输入信号的主峰。

提出的SF-SLSN是一种BD方法，通过采用广义Lp/Lq范数（G-Lp/Lq）来恢复稀疏
了克服这些最优准则的局限性，提出了一些基于故障周期信息的最优准则，包括相关峰度（CK）、多D范数multi D-norm（MDN）和循环平稳性指标（ICS）。MCKD、MOMEDA和CYCBD分别是基于CK、MDN和ICS的典型BD技术。
另一种基于信号平方包络(SE)的最优判据是表征非平稳信号尤其是轴承故障信号冲量的有效判据，包括谱峭度(SK)[8]、谱L2/L1范数[24]、谱Lp/Lq范数[24]、谱平滑指数[25]、谱Gini指数。
为了充分利用ES在表征环平稳性信号方面的优势，本研究开展了以下工作。首先，本研究提出了一种新的BD技术，用于从ES中提取重复瞬态的循环平稳性。新方法通过最小化由ES定义的最优标准来搜索滤波器，而不是最小化由时域波形或SE定义的最优标准。（就是通过使用ES定义的最优准则提供了一个反卷积的算法框架），本文的内容还有介绍了所提出的以G-Lp/Lq范数为最优准则的BD方法。它展示了如何设计BD算法来从ES中提取重复瞬态的循环平稳性。这种基于G-Lp/Lq范数的BD方法是一种非参数方法，对异常值具有良好的鲁棒性。

理论
试图通过使滤波信号的最优准则最大化或最小化来追求一个反滤波器来抵消传输路径的影响，可以表示为:

y表示测量信号，f是期望的反滤波器，x是由反滤波器f获得的滤波信号，∗表示卷积算子。为了便于数值计算，将Eq.(1)的卷积过程重构为矩阵乘法的形式:

其中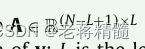

是由y导出的Hankel矩阵;N是y的长度;L是反滤波器f的长度。为了利用ES判据实现BD，需要将滤波后的信号x转换成ES。平方包络线e可以定义为:

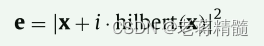
hilbert (x)表示滤波后信号的hilbert变换(HT);|·|为模算子。对于向量x， | x |的模是通过使用恒等式
得到的，其中圆圈点表示元素积，conj (x)是x的复共轭。

G- Lp/Lq范数代表了一大类稀疏测度，包括峰度、L2/L1范数[5]、偏态[35]、Gary变量范数(p > 2和q = 2)[20]和pq均值范数(0 < p < 1和q > 1)[21]。G- Lp/Lq范数具有很强的灵活性，其特性完全由变量p和q决定。G- Lp/Lq范数Lp,q的定义为:

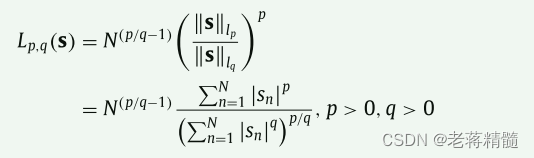
中s为输入信号;N是s的长度。将项N (p/ q−1)加入式(14)的目的是得到归一化GLp/Lq范数。G- Lp / Lq具有很强的灵活性，可以表示许多常用的稀疏准则。

械设备的几种常用健康指标

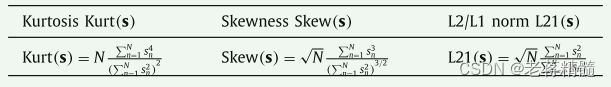
提出方法的流程

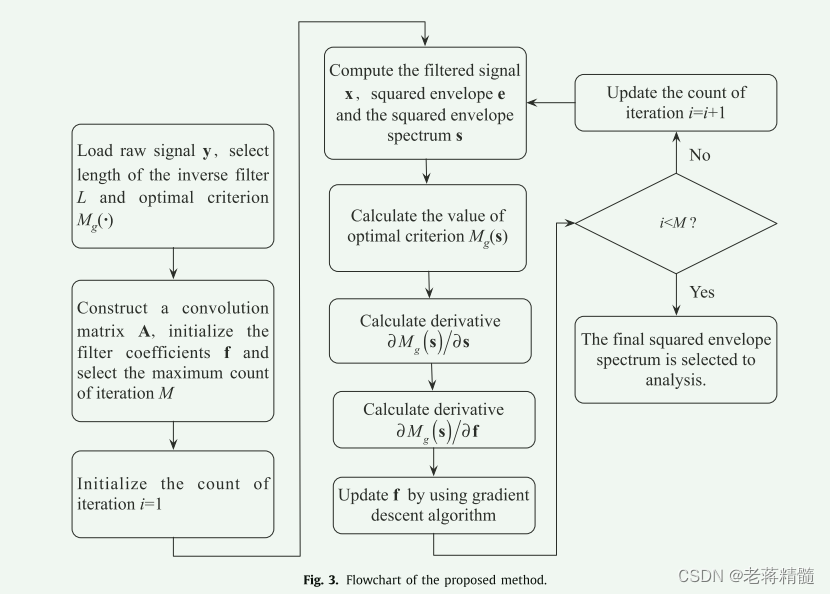
案例：
引入一个模拟的轴承故障信号来说明所提方法的有效性。为了突出该方法的优点，将其结果与传统的基于MED和SF-SLSN的时域BD进行了比较。MED和SF-SLSN在MATLAB中的实现可以在外部资源部分中找到。模拟信号：

a(t)是故障阐述的故障脉冲信号，

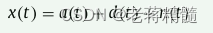
d(t)是随机脉冲

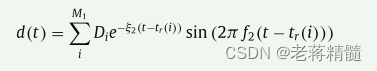
n(t)是随机噪声
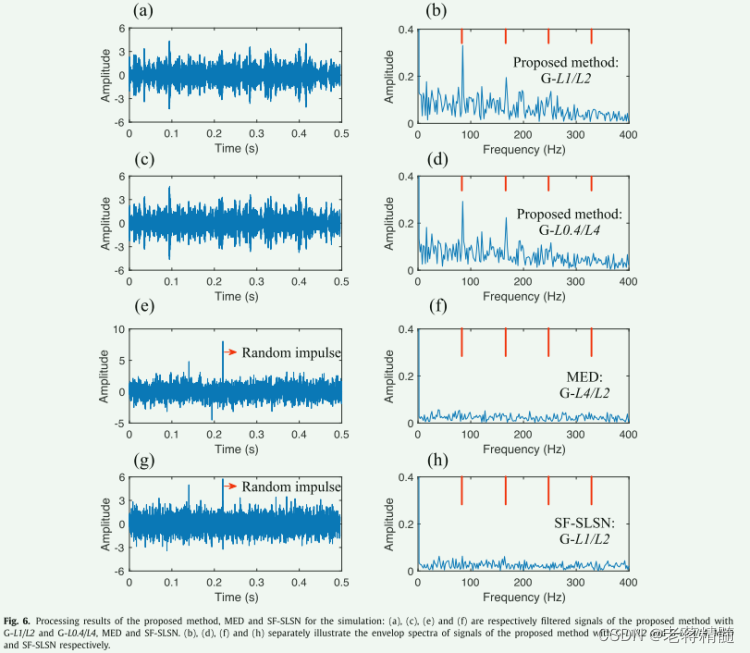
将模拟脉冲信号、随机脉冲信号、噪声信号和混合信号分别绘制在图4 (a)至(d)中，从图4 (d)的观察可以看出，重复脉冲信号完全淹没在噪声背景中，混合信号中的随机脉冲明显。图5为混合信号的ES。ES中的红线对应故障特征频率及其谐波。从图5可以看出，故障特征频率很难识别。

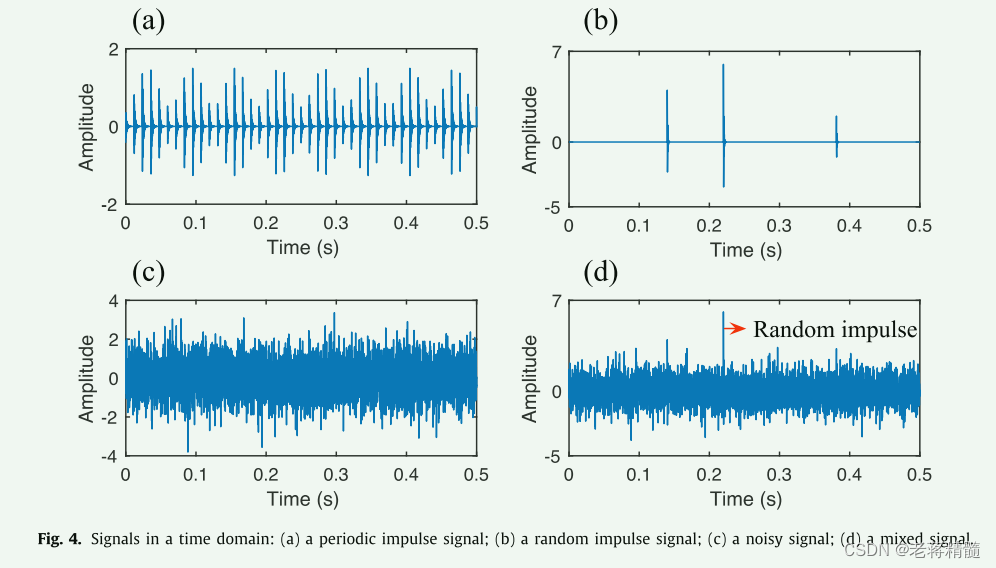
处理结果分别如图6（a）、（b）、（c）和（d）所示。在这种情况下，所提出的方法选择了G-L1/L2范数（p=1，q=2）和G-L0.4/L4范数（p=0.4，q=4）。 过滤器长度设置为 L=40。事实上，其他 p、q 值仍然是可选的。关于p和q的选择策略，请参考文献[15]。为了验证所提方法的优越性，采用基于MED和SF-SLSN的时域BD方法对混合信号进行处理。然后，滤波器长度 L 也设置为 40。MED和SF-SLSN得到的处理结果分别如图6（e）、（f）、（g）和（h）所示。从图6（a）、（c）、（e）和（g）可以看出，图6（a）和（c）具有明显的脉冲特性。然而，图6（e）和（g）中出现了一个大振幅的单脉冲。这些结果表明，MED和SF-SLSN对单个脉冲很敏感，这往往会过度突出输入信号中的主峰。相比之下，所提出的方法对随机脉冲具有鲁棒性。所提方法MED和SF-SLSN得到的信号包络谱分别绘制在图6（b）、（d）、（f）和（h）中。图6（b）和（d）中通过所提方法得到的包络谱表明了不同的故障谐波。该结果清楚地揭示了模拟的轴承故障。然而，MED和SF-SLSN得到的包络谱中的谱线非常混乱，很难观察到与故障特征频率相关的谐波，如图6（f）和（h）所示。正因为如此，时域中随机脉冲（异常值）的频谱类似于谱线分布均匀的“均匀谱”，因此基于ES定义的最优准则的BD不会收敛到时域随机脉冲。对图6（b）和（d）的结果进行比较，可以看出G-L1/L2范数和G-L0.4/L4范数的结果相似。这意味着结果的稀疏性受 p/q 比的影响较小。

测试主函数代码

%% demo 
clc
clear all
close all
addpath('./minFunc');
N=5000;
Fs=10000;  % sampling frequency
fts=[0:1:N-1]*Fs/N;
t=[0:1:N-1]/Fs;
load('sim_fault.mat');
load('sim_outlier.mat');
load('sim_noise.mat');
sx1=sim_fault+sim_outlier+sim_noise;
%%
close all
aa=300;bb=150;
figure(1)
plot(t,sim_fault,'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Time (s)','fontsize',12)
title("sim_fault");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);
ylim([-2,2])

figure(2)
plot(t,sim_outlier,'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Time (s)','fontsize',12)
title("sim_outlier");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);
ylim([-5,7])
yticks([-5,0,7])

figure(3)
plot(t,sim_noise,'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Time (s)','fontsize',12)
title("sim_noise");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);

figure(4);
plot(t,sx1,'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Time (s)','fontsize',12)
title("sim_fault+sim_outlier+sim_noise");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);
ylim([-5,7])
yticks([-5,0,7])
%%
figure(5)
plot(fts,abs(fft(sx1))*2/N,'LineWidth',1)
xlabel('Frequency (Hz)','fontsize',12)
ylabel('Amplitude','fontsize',12)
title("FFT");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,300,150]);
% ylim([0,0.3])
xlim([0,5000])
figure(6)
plot(fts,abs(fft(abs(hilbert(sx1))))*2/N,'LineWidth',1)
xlabel('Frequency (Hz)','fontsize',12)
ylabel('Amplitude','fontsize',12)
title("hilbert_trans");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
%set(gcf,'position',[200,300,300,150]);
ylim([0,0.1])
xlim([0,800])
set(gcf,'position',[200,300,600,200]);

%%
[~,rec1]=min_blp_lplq(sx1,40,0,1,2);
fts1=(0:length(rec1)-1)*Fs/length(rec1);
NN=length(rec1);
figure(7)
plot(t(1:NN),rec1,'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Time (s)','fontsize',12)
title("min_blp_lplq(rec1)");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);
ylim([-6,6])
yticks([-6:3:6])

figure(8)
plot(fts1,abs(fft(abs(hilbert(rec1))))*2/length(rec1),'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Frequency (Hz)','fontsize',12)
title("hilbert(rec1))");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);
xlim([0,400]);
ylim([0,0.4])
%%
[~,rec2]=min_blp_lplq(sx1,40,0,0.4,4);
fts1=(0:length(rec2)-1)*Fs/length(rec2);
NN=length(rec2);
figure(9)
plot(t(1:NN),rec2,'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Time (s)','fontsize',12)
title("min_blp_lplq(rec2)");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);
ylim([-6,6])
yticks([-6:3:6])

figure(10)
plot(fts1,abs(fft(abs(hilbert(rec2))))*2/length(rec2),'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Frequency (Hz)','fontsize',12)
title("hilbert(rec2))");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);
xlim([0,400]);
ylim([0,0.4])
%%
[y_final] =med2d(sx1,40,400,0.0001,0);
fts1=(0:length(y_final)-1)*Fs/length(y_final);
NN=length(y_final);
figure(11)
plot(t(1:NN),y_final,'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Time (s)','fontsize',12)
title("med2d(y_final))");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);
ylim([-5,10])
yticks([-5:5:10])

figure(12)
plot(fts1,abs(fft(abs(hilbert(y_final))))*2/length(y_final),'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Frequency (Hz)','fontsize',12)
title("(hilbert(y_final)");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);
xlim([0,400]);
ylim([0,0.4])

%%
[~,rec3]=min_lplq(sx1,40,0,1,2);
fts1=(0:length(rec3)-1)*Fs/length(rec3);
NN=length(rec3);
figure(13)
plot(t(1:NN),rec3,'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Time (s)','fontsize',12)
title("min_lplq(rec3)");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);
ylim([-6,6])
yticks([-6:3:6])

figure(14)
plot(fts1,abs(fft(abs(hilbert(rec3))))*2/length(rec3),'LineWidth',1)
ylabel('Amplitude','fontsize',12)
xlabel('Frequency (Hz)','fontsize',12)
title("hilbert(rec3)");
set(gca,'linewidth',1);
set(gca,'FontSize',12);
set(gcf,'position',[200,300,aa,bb]);
xlim([0,400]);
ylim([0,0.4])