第二章线性表【数据结构与算法】【精致版】

前言
版权
第二章线性表
- 2.1 应用实例
- - 应用实例一约瑟夫环问题(Josephus problem)
  - 应用实例二一元多项式运算器
- 2.2 线性表的概念及运算
- - 2.2.1线性表的逻辑结构
  - 2.2.2 线性表的运算
- 2.3 线性表的顺序存储
- - 2.3.1 顺序表
  - 2.3.2 顺序表的基本运算
  - - **1-顺序表.h**
    - [例 2-1] 两个顺序表合并
    - [算法2-5] 两个顺序表合并
- 2.4 线性表的链式存储
- - 2.4.1 单链表
  - 2.4.2 单链表基本运算
  - - **2-单链表.h**
    - [例2-2]单链表的逆置
    - [例2-3]单链表中删除重复结点
    - [例2-4]两个集合的差集
    - [例] 两个单链表的合并
  - 2.4.3 循环链表(自学）
  - - **3-循环链表.c**
  - 2.4.4 双向链表(自学）
  - - **4-双向链表.c**
  - 2.4.5 静态链表(自学）
  - - **5-静态链表**
- 2.5 顺序表和链表的比较
- 2.6 实例分析与实现
- - 约瑟夫环
  - 一元多项式运算器
实验
- - 约瑟夫环
  - - **约瑟夫环.c**
  - 一元多项式运算器
  - - **多项式.c**
习题2
- 1.单项选择题
- 2.算法设计题
- - (1) 设有一线性表e=(e1,e2,...,e[n-1],en,其逆线性表定义为e'=(en,e[n-1],...,e2,e1)。请设计一个算法,将线性逆置,要求逆线性表仍占用原线性表的空间,并且用顺序表和单链表两种方法来表示,写出不同的处理函数。
  - (3) 已知线性表A的长度为n,并且采用顺序存储结构。请编写算法，删除线性表中所有值为x的元素。
  - (5) 假设有一个循环链表的长度大于1,且表中既无头结点也无头指针。已知s为指向链表中某结点的指针，试编写算法,在链表中删除指针s所指结点的前驱结点。
  - (8)设指针la和lb分别指向两个无头结点单链表中的首元结点,试设计算法,从表la中删除自第i个元素起共len个元素,并将它们插入表lb的第j个元素之后。
  - (9)设带头结点的线性单链表A=(a1,a2,...,am),B=(b1,b2,...bn)。试编写算法按下列规则合并A、B为线性单链表C,使得
最后

前言

2023-11-2 14:33:08
以下内容源自《【数据结构与算法】【精致版】》
仅供学习交流使用

版权

禁止其他平台发布时删除以下此话
本文首次发布于CSDN平台
作者是CSDN@日星月云
博客主页是https://jsss-1.blog.csdn.net
禁止其他平台发布时删除以上此话

第二章线性表

2.1 应用实例

应用实例一约瑟夫环问题(Josephus problem)

约瑟夫环问题是由古罗马的史学家约瑟夫提出的。问题描述为:编号为1,2.,n的n个人按顺时针方向围坐在一张圆桌周围,每人持有一个密码(正整数)。一开始任选一个正整数作为报数上限值m,从第一个人开始按顺时针方向自1开始报数,报到m时停止报数,报m的那个人出列,将其密码作为新的m值,并从其顺时针方向的下一个人开始重新从1报数,数到m的那个人又出列;如此下去,直至圆桌周围的人全部出列为止。这个游戏的实现只需将每个人的信息什为一个结点,结点中存放每个人的编号和密码。由于要反复做删除操作,所以采用单向循环链表实现比较方便,详见本章2.6节。

应用实例二一元多项式运算器

要实现一元多项式运算器,首先要设计表示一元多项式P=p0+p1x+p2x^2+…+pn x^n"的合适的数据结构,并支持多项式的下列运算。

建立多项式。
输出多项式。
+,两个多项式相加,建立并输出和多项式。
-,两个多项式相减,建立并输出差多项式。
*,多项式乘法。
(),求多项式的值。
derivative(),求多项式导数。

这个问题看起来很复张,但只要用本章将要学习的带头结点的单链表来存储多项式，头结点中存放多项式的参数(如项数等),问题就可以迎刃而解。详细的实现分析及算法见本章2.6节。

2.2 线性表的概念及运算

2.2.1线性表的逻辑结构

线性表是n(n>=0)个数据元素的有限序列。在表中，元素存在线性的逻辑关系：表中有且仅有一个开始结点;有且仅有一个终端结点；除开始结点外，表中的每个结点均只有一个前驱结点(predecessor);除终端结点外，表中的每个结点均只有一个后继结点(successor)。根据它们之间的关系可以排成一个线性序列,记作（a1,a2,…,an）

2.2.2 线性表的运算

基本操作

① InitList(L) 			线性表初始化,构造一个空的线性表L。
② ListLength(L)			求线性表的长度,返回线性表L中数据元素的个数 
③ GetElem(L,i,x)		用x返回线性表中的第i个数据元素的值。
④ locaionElem(L,x)		按值查找,确定数据元素x在表中的位置。  
⑤ ListInsert(L,i,x)		插入操作,在线性表L中第i个位置之前插入一个新元素。L的长度加1。
⑥ ListDelete(L,i)		删除操作,删除线性表L中的第i个元素,L的长度减1。  
⑦ ListEmpty(L)			判断线性表L是否为空,空表返回TRUE,非空表返回FALSE。  
⑧ ClearList(L)			将已知的线性表L置为空表。
⑨ DestroyList(L)			销毁线性表L。

其他操作：合并、分拆、复制、排序等等。

2.3 线性表的顺序存储

2.3.1 顺序表

顺序存储是指在内存中用一块地址连续的存储空间按顺序存储线性表的各个数据元素。采用顺序存储结构的线性表称为“顺序表”顺序表中逻辑上相邻的数据元素在物理存储位置上也是相邻的。

#define MAXSIZE <线性表可能达到的最大长度>  
typedef int ElemType;
typedef struct
{ 	ElemType elem[MAXSIZE];
	int length;//线性表长度
} SeqList;

2.3.2 顺序表的基本运算

1-顺序表.h

# include <stdio.h>
# include <stdlib.h>
# include <string.h>
//函数结果状态代码 
#define TRUE 1 
#define FALSE 0
#define OK 1 
#define ERROR 0
#define INFEASIBLE -1 
#define OVERFLOW -2 


typedef int Status;
typedef int Boolean; 

#define MAXSIZE 255
typedef int ElemType;

typedef struct{
	ElemType elem[MAXSIZE];//下标从1开始，0没有值 
	int length;//线性表长度 
} SeqList; 

//1.顺序表的初始化
//【算法2-1】 顺序表的初始化
void Init(SeqList *L){
	L->length=0;

} 


//创建顺序表函数 初始化前n个数据
int CreateList(SeqList *L, int n)
{
	printf("创建顺序表\n");
	printf("依次输入%d个值\n",n);
	int i;
	if (n<0 || n>MAXSIZE) return FALSE;//n非法
	for ( i = 1; i<=n; i++)
	{
		scanf("%d",&(L->elem[i]));
		L->length++;
	}
	return TRUE;
}



//2.顺序表的插入 
//【算法2-2】顺序表的插入 
int Insert(SeqList * L,int i,ElemType x){
	
	int j;
	if(L->length==MAXSIZE-1){		//表空间已满,不能插入 
		printf("表满");
		return OVERFLOW;
	}
	if(i<1||i>L->length+1){		//检查插入位置的正确性
		printf("位置错");
		return ERROR;
	}
	
	//使得后一个的值覆盖为前一个的值 
	for(j=L->length;j>=i;j--){
		L->elem[j+1]=L->elem[j];
	}
	L->elem[i]=x;
	L->length++;
	return TRUE;//插入成功,返回
}

//3.顺序表的删除
//【算法2-3】 顺序表的删除
//删除表中第i个元素，若表空或不存在指定元素，则返回ERROR

int Delete(SeqList* L, int i, ElemType *e){
		
	int j; 
	
	if(i<1||i>L->length){	//检查空表及删除位置的合法性
		printf("不存在第i个元素");  
		return ERROR;
	
	}
	*e=L->elem[i];//存储待删除的元素值
	for (j=i;j<=L->length-1;j++){
		L->elem[j]=L->elem[j+1];//向上移动 
	}
	
	L->length--;
	return TRUE;//删除成功,返回
}
//4.顺序表中的按值查找 
//【算法2-4】顺序表中的按值查找 
int Location( SeqList * L, ElemType x){
	int i=1;
	while(i<=L->length && L->elem[i]!=x)
		i++;
	if(i>L->length)  return FALSE;	//错误 
	else return i;//返回x的存储位置
} 
//5.另外
//按序号查询 ,结果返回由x实现 
int GetElem(SeqList *L,int i,ElemType *x) {
	
	if(i<1||i>L->length)  return ERROR;	//查找失败
	else{
		*x=L->elem[i];
		return TRUE;
	} 
}
//求表长 
int ListLength(SeqList *L){
	return L->length;
}
//遍历输出 
void Output(SeqList* L){
	int i=1;
	for(i;i<=L->length;i++){
		printf("%d ",L->elem[i]);
	}
	printf("\n") ;
}

1-顺序表测试.c

#include "1-顺序表.h"

int main(){

	SeqList _L;
	SeqList *L=&_L;

	//初始化 
	Init(&_L);
	
	int n=0; 
	printf("输入创建的元素个数:");
	scanf("%d",&n);
	
	//创建 
	CreateList(L,n);
	
	printf("输出顺序表:");
	Output(L);
	
	//插入 
	printf("在1处插入1\n"); 
	Insert(L,1,1);
	printf("在2处插入2\n"); 
	Insert(L,2,2);
	printf("插入之后"); 
	Output(L);
	printf("表长:%d\n",ListLength(L));
	
	//删除
	printf("删除1\n"); 
	ElemType d=-1;
	Delete(L,1,&d);
	printf("删除之后"); 
	Output(L);
	
	//查询
	printf("查询1\n"); 
	ElemType x=1;
	int i=Location(L,x);
	printf("序号%d\n",i);
	
	printf("按索引i查询\n"); 
	ElemType y;
	GetElem(L,i,&y);
	printf("值%d",y); 
}

运行结果如下

在这里插入图片描述

[例 2-1] 两个顺序表合并

有两个顺序表LA和LB，其元素均为非递减有序排列, 编写一个算法，将它们合并成一个顺序表LC，要求LC也是非递减有序排列。

算法思路:依次扫描A和B的元素，比较当前元素的值，将较小值的元素赋给C,如此直到一个线性表扫描完毕,然后将未外理完的顺序表的余下部分元麦连在表C的后面即可。表C的容量要能够容纳A、B两个线性表中的所有元素。

[算法2-5] 两个顺序表合并

2-5顺序表的合并.c

#include "1-顺序表.h"

// [例 2-1] 两个顺序表合并 
//【算法2-5】两个顺序表的合并
void merge(SeqList* A, SeqList* B,SeqList* C)
{	int i,j,k;
	i=1;j=1;k=1;
	while (i<=A->length && j<= B->length)
		if (A->elem[i]<=B->elem[j])
			C->elem[k++]=A->elem[i++];
		else C->elem[k++]=B->elem[j++];
	while (i<=A->length)
		C->elem[k++]=A->elem[i++];
	while (j<=B->length)
		C->elem[k++]=B->elem[j++];
	C->length=A->length+B->length;
}



int main(){
	SeqList _L1;
	SeqList *L1=&_L1;

	//初始化L1
	Init(&_L1);
	
	SeqList _L2;
	SeqList *L2=&_L2;

	//初始化L2
	Init(&_L2);
	
	int n=0; 
	
	printf("输入创建L1的元素个数:");
	scanf("%d",&n);
	//创建L1
	printf("创建非递减的L1"); 
	CreateList(L1,n);


	printf("输入创建L2的元素个数:");
	scanf("%d",&n);	
	//创建L2
	printf("创建非递减的L2"); 
	CreateList(L2,n);
	
	printf("输出顺序表L1:");
	Output(L1);		
	
	printf("输出顺序表L2:");
	Output(L2);		
	
	
	SeqList _L3;
	SeqList *L3=&_L3;
	//初始化L3
	Init(&_L3);
	
	//L1和L2合并为L3 
	printf("L1和L2合并为L3\n");
	merge(L1,L2,L3);
	
	printf("输出顺序表L3:");
	Output(L3);		 
}

算法的时间复杂度是0(m+n),其中m是A的表长,n是B的表长。

在这里插入图片描述

2.4 线性表的链式存储

链式存储，通过“链”建立起数据元素之间的逻辑关系，这种用链接方式存储的线性表简称链表（link list）。

2.4.1 单链表

链表中的每一个结点都至少包括两个与，一个域存储数据元素信息，称为“数据域”；另一个域存储之间后继元素的地址，称为“指针域”。
结点定义如下：

typedef struct code 
{	DataType data;//数据域
	struct node * next;//指针域
}LNode,*LinkList;

n个元素的线性表通过每个结点的指针域连接成了一条“链子”,故形象地称之为“链表”。因为每个结点中只有一个指向其直接后继的指针所以称其为单链表。

2.4.2 单链表基本运算

2-单链表.h

#include<stdio.h>
#include<stdlib.h>
#include<string.h> 
#define DataType int
#define ERROR 0
#define TRUE 1

typedef struct node{
	DataType data;
	struct node *next;
}LNode,*LinkList;
//初始化单链表 
//LinkList InitList(){
//	LinkList head;
//	head=(Node*)malloc(sizeof(Node)); 
//	head->next=NULL;
//	return head; 
//}
//1.建立单链表
//【算法2-6】头插法建立单链表 
LinkList CreatByHead() {
	LinkList H=(LinkList)malloc(sizeof(LNode)); //生成头结点 
	H->next=NULL;		//空表 
	LNode *s;
	printf("输入（-1结束）"); 
	int x;	
	scanf("%d",&x);
	while(x!=-1){
		s=(LinkList)malloc(sizeof(LNode));
		s->data=x;
		s->next=H->next;
		H->next=s;
		printf("输入（-1结束）"); 
		scanf("%d",&x);
	}
	 return H;
}
//【算法2-7】尾插法建立单链表 
LinkList CreatByBear(){
	LinkList H=(LinkList)malloc(sizeof(LNode)); //生成头结点 
	H->next=NULL;		//空表 
	LNode *s, *r=H;
	int x;
	printf("输入（-1结束）"); 
	scanf("%d",&x);
	while(x!=-1){
		s=(LinkList)malloc(sizeof(LNode));
		s->data=x;
		
		r->next=s;
		r=s;		//r指向新的尾结点 
		printf("输入（-1结束）"); 
		scanf("%d",&x);
	}
	 r->next=NULL;   
	 return H;
}
//2.求表长
//【算法2-8】 求单链表的表长
int Length(LinkList H){
	LNode *p=H;   //p指向头结点
	int j=0;
	while(p->next!=NULL)  {
		p=p->next;
		j++;
	} 
	return j;
} 

//3.查找操作 
//(1) 按序号查找  Get(H,k)
//【算法2-9】单链中按序号查找 
LinkList Get(LinkList H,int k){
	LNode *p=H;
	int j=0;
	while(p->next!=NULL&&j<k){
		p=p->next;
		j++;
	}

	if(j==k )return p;
	else return NULL;
	
}
//(2) 按值x查找 
//【算法2-10】单链中按值查找 
LNode *Locate(LinkList H,DataType x){
	LNode *p=H->next;
	while(p!=NULL&&p->data!=x){
		p=p->next;		
	}
	return p;	
}
//4.插入操作 
//后插 
//*s插入到*p后 
/*
s->next=p->next;
p->next=s;
*/ 
//前插
//*s插入到*p前
/*
q=H;
while(q->next!=p)	//找*p的直接前驱q
	q=q->next;
s->next=p;
q->next=s;	//插入 
*/ 
//【算法2-11】单链表的插入 
//在单链表H的第i个位置上插入值为x的元素 
int Insert(LinkList H,int i,DataType x){
	LNode *p,*s;
	p=Get(H,i-1);  //查找第i-1个结点
	if(p==NULL) {   //第i-1个结点不存在，不能插入 
		printf("插入位置i错") ;
		return ERROR; 
	} else{
		s=(LinkList)malloc(sizeof(LNode));//申请新结点 
		s->data=x; 
		s->next=p->next;   //新结点插入 第i-1个结点 后 
		p->next=s;
		return TRUE;
	}
	


}
//删除操作 
//【算法2-12】  单链表的删除 
int Delete(LinkList H,int i){//删除单链表H上的第i个数据结点 
	LinkList p,q;
	p=Get(H,i-1);
	if(p==NULL) {   //第i-1个结点不存在，不能插入 
		printf("第i-1个结点不存在"); 
		return ERROR; 
	}
	else{
		if(p->next==NULL){
			printf("第i个结点不存在"); 
			return ERROR; 
		}
		else{
			q=p->next;    //指向第i个结点 
			p->next=q->next;	//从链表中删除 
			free(q);		//释放*q 
			return TRUE;
		}
	} 

} 

//遍历输出 
void OutPut(LinkList head){
	LNode *p;
	p=head->next;
	while(p){		
		printf("(%d)\n",p->data);
		p=p->next;
	}
}

#include"2-单链表.h" 


void main(){
	//建立 
	LinkList h=CreatByBear();
	OutPut(h);
	//插入 
	printf("在1处插入1\n"); 
	Insert(h,1,1);
	printf("在2处插入2\n"); 
	Insert(h,2,2); 
	printf("插入之后\n"); 
	OutPut(h);
	
	//删除 
	printf("删除2\n"); 
	Delete(h,2);
	printf("删除之后\n"); 
	OutPut(h);
	
	//按序号查询 
	LNode *p;
	p=Get(h,1);
	printf("按序号查找到的信息如下：\n");
	printf("%d\n",p->data);
	//按值查询
	LNode *s;
	s=Locate(h,1);
	printf("按值查找到的信息如下：\n");
	printf("%d\n",s->data);
}

运行结果如下
在这里插入图片描述

[例2-2]单链表的逆置

2-13单链表的逆置.c

#include"2-单链表.h"

//补充 
//【算法2-13】 单链表的逆置
void Reverse(LinkList H){  
	LNode * p,*q;
	p=H->next;		//p指向第一个数据结点
	H->next= NULL;		//将原链表置为空表H
	while(p){
		q=p;
		p=p->next;
		q->next=H->next;	//将当前结点插到头结点的后面(头插)
		H->next=q;
	}

} 


int main(){
	//建立 
	printf("单链表的建立:\n");
	LinkList h=CreatByBear();
	OutPut(h);
	//逆序 
	printf("单链表的逆置:\n");
	Reverse(h);
	OutPut(h);		
}

运行结果
在这里插入图片描述

[例2-3]单链表中删除重复结点

2-14单链表中删除重复结点.c

书上有一处错误
while(p->next)此处应该为whlie(p)

#include"2-单链表.h"

// [例2-3]单链表中删除重复结点
//【算法2-14】单链表中删除重复结点
void pur_LinkList(LinkList H){
	LNode *p,*q,*r;
	p=H->next;//p 指向第一个结点
	if(p!=NULL){
		while(p){
			q=p;
			while(q->next){//从*p的后继开始找重复结点
				if(q->next->data==p->data){
					r=q->next;//找到重复结点,用r指向,删除*r
					q->next=r->next;
					free(r);
				}else{
					q=q->next;
				}
			}//while(q->next)
			p=p->next;//p指向下一个结点,继续
		}//while(p->next)
	}
	
}

int main(){
	printf("单链表的建立:\n");
	//建立 
	LinkList h=CreatByBear();
	OutPut(h);
	printf("单链表中删除重复结点:\n");
	pur_LinkList(h);
	OutPut(h);	
}

运行结果
在这里插入图片描述

[例2-4]两个集合的差集

#include"2-单链表.h"

//  [例2-4]两个集合的差集
// 【算法2-15】两个集合的差集

void Difference(LinkList LA,LinkList LB){//此算法求两个集合的差集
	LNode* pre,*p,*r;
	pre=LA;
	p=LA->next;//p向表中的某一结点,pre 始终指向 p的前驱
	while(p!=NULL){	
		LNode* q=LB->next; //扫描 LB 中的结点,寻找与 LA中*p结点相同的结点
		while(q!=NULL&&q->data!=p->data){	
			q=q->next;
		}
		if(q!=NULL){
			r=p;
			pre->next=p->next;
			p=p->next;
			free(r);
		}else{
			pre=p;
			p=p->next;
		}
	}
}

int main(){
	//建立 
	printf("单链表h1的建立:\n");
	LinkList h1=CreatByBear();
	OutPut(h1);	
	
	printf("单链表h2的建立:\n");
	LinkList h2=CreatByBear();	
	OutPut(h2);
	
	printf("h1和h2的差集:\n");
	Difference(h1,h2);
	OutPut(h1);	
}

运行结果
在这里插入图片描述

[例] 两个单链表的合并

有两个单链表LA和LB，其元素均为非递减有序排列, 编写一个算法，将它们合并成一个单链表LC，要求LC也是非递减有序排列。
要求:新表LC利用原表的存储空间。

#include"2-单链表.h"

// [例] 两个单链表的合并
// 两个单链表的合并
LinkList MergeLinkList(LinkList LA,LinkList LB)
{
	LNode *pa,*pb;
	LinkList LC;
	pa=LA->next;
	pb=LB->next;
	LC=LA;
	LC->next=NULL;
	LNode* r=LC;
	while(pa&&pb)
	{  
		if(pa->data<=pb->data)
		{	
			r->next=pa;
			r=pa;
			pa=pa->next;  
		}
		else
		{  
			r->next=pb;
			r=pb;
			pb=pb->next; 
		}
	}
	if(pa) r->next=pa;
	else  r->next=pb;
	free(LB);
	return(LC);
}

int main(){
	//建立 
	printf("单链表h1的建立:\n");
	LinkList h1=CreatByBear();
	OutPut(h1);
	
	printf("单链表h2的建立:\n");
	LinkList h2=CreatByBear();
	OutPut(h2);	
	
	//合并
	printf("h1和h2合并为h3:\n");
	LinkList h3=MergeLinkList(h1,h2);
	OutPut(h3);	
}

在这里插入图片描述

2.4.3 循环链表(自学）

循环单链表的操作与单列表基本一致，不同之处在于单链表的循环结束条件是p或p->next为空，而循环单链表的判断条件是它们是否等于头指针。

3-循环链表.c

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct node{				//链表结点结构体定义 
	int number;			//数字 
	struct node *next;	//*next的类型是指向本结构体类型的指针 
	
}Node,*LinkList; 

LinkList InitList(){      			//单链表初始化函数   
	LinkList head;
	head=(Node*)malloc(sizeof(Node));	//分配头结点的内存空间 
	head->next=NULL;					//头结点的指针域为空 
	return head;						//返回头结点的地址，即头指针	 
}

void CreatByRear(LinkList head){      //尾插法创建单链表  
	Node *r,*s; 
	int number;
	r=head;				//r指向头结点 
	while(1){
		printf("请输入数字(0停止)：\n");
		
		scanf("%d",&number);
		if(number==0)
		break;
		s=(Node*)malloc(sizeof(Node));//分配结点的内存空间
		
		s->number=number;
		r->next=s;			//原来的结点指向新结点 
		r=s;				//r指向新结点 
	} 
	r->next=head;			//链表的尾结点指针指向头结点 
} 

void OutPut(LinkList head) 	{						//输出单链表   284页 
	Node *p;			//循环所用的临时指针
	p=head->next;       //*p指向链表的首元结点
	printf("\n*******打印*******\n");
	while(p!=head){
		printf("数字：%d\n",p->number);   //输出学号
		p=p->next;  		//移动临时指针到下一个结点 
	}
	
}	 


void main(){
	LinkList ha;   			//定义单链表头指针		
	ha=InitList();			//初始化单链表
	CreatByRear(ha);        //尾插法创建单链表
	OutPut(ha);				//输出单链表	
}

运行结果如下
在这里插入图片描述

2.4.4 双向链表(自学）

结点定义如下

typedef struct dlnode{
	DataType data;
	Struct dlnode *prior,*next;
}DLNode,*DLinkList;

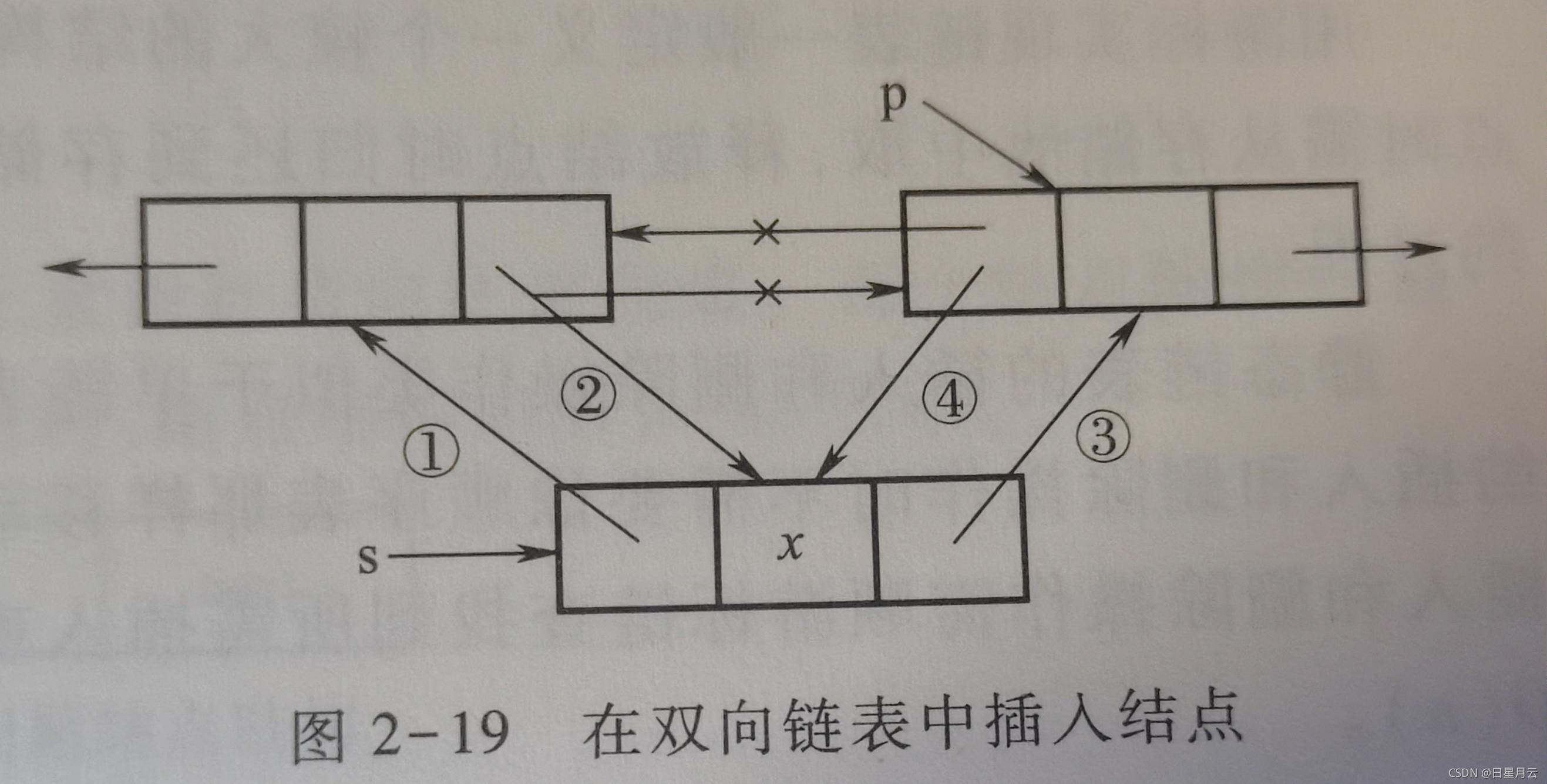
1.双向链表中结点的插入操作
设p指向链表中的某结点,s指向待插入的新结点,将s插在p的前面,尤其要注意操作顺序,操作过程如下。

①s->prior=p->prior;
② p->prior->next=s;
③s->next=p;
④p->prior=s;

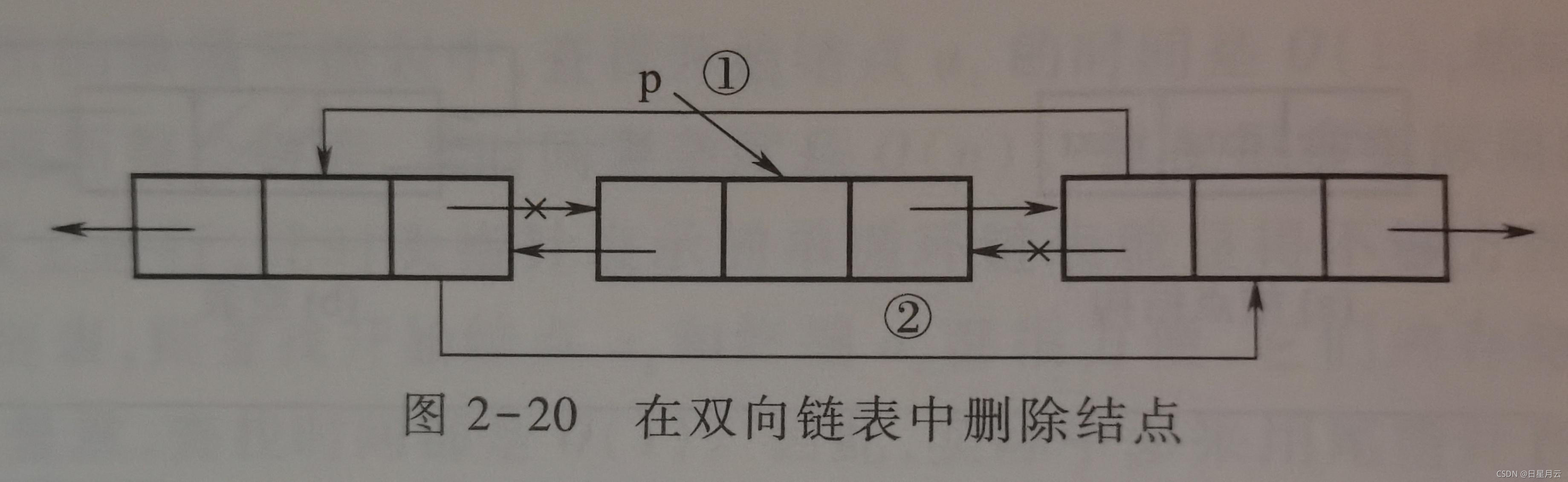
请添加图片描述

2.双向链表中结点的删除操作
设p指向双向链表中待删除的结点,操作过
程如图所示。具体如下。

①p->prior->next=p->next;
②p->next->prior-p->prior;
③free(p);

请添加图片描述

4-双向链表.c

增删插

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct node{				//链表结点结构体定义 
	int number;			//数字 
	struct node *prior;
	struct node *next;	//*next的类型是指向本结构体类型的指针 
	
}Node,*LinkList; 

LinkList InitList(){      			//单链表初始化函数   
	LinkList head;
	head=(Node*)malloc(sizeof(Node));	//分配头结点的内存空间 
	head->next=NULL;					//头结点的指针域为空 
	return head;						//返回头结点的地址，即头指针	 
}

void CreatByRear(LinkList head){      //尾插法创建单链表  
	Node *r,*s;
	int number;
	r=head;				//r指向头结点 
	
	while(1){
		printf("请输入数字（0结束）：\n");
		scanf("%d",&number);
		if(number==0)
		break;
		s=(Node*)malloc(sizeof(Node));//分配结点的内存空间
		s->number=number;
		r->next=s;			//原来的结点指向新结点 
		s->prior=r; 		//新结点的上一个结点是r 
		r=s;				//r指向新结点 
	} 
	r->next=NULL;			//链表的尾结点指针置为空 
} 

void OutPut(LinkList head) 	{						//输出单链表   
	Node *p;			//循环所用的临时指针
	p=head->next;       //*p指向链表的首元结点
	printf("\n*******打印*******\n");
	while(p){
		printf("数字：%d\n",p->number);   //输出学号
		p=p->next;  		//移动临时指针到下一个结点 
	}
	
}	 

void Insert(LinkList head,int i){
	Node *s;
	Node *p=head;
	int j=0;
	while(p->next!=NULL&&j<i){
		p=p->next;
		j++;
	}
	if(j!=i){
		p=NULL;
	}
	if(p==NULL){
		printf("插入位置错误\n");
		return;
	}else{
		
		int number;
		s=(Node*)malloc(sizeof(Node));
		printf("输入插入结点的数字：");
		scanf("%d",&number);
		s->number=number;
		
		s->prior=p->prior;
		p->prior->next=s;
		s->next=p;
		p->prior=s;
		 
	}
} 

void Delete(LinkList head,int pos){
	Node *s;
	Node *p=head;
	int j=0;
	while(p->next!=NULL&&j<pos){
		p=p->next;
		j++;
	}
	if(j!=pos){
		p=NULL;
	}
	if(p==NULL){
		printf("删除位置错误\n");
		return;
	}else{
		
		p->prior->next=p->next;
		p->next->prior=p->prior;
	
		free(p);
		 
	}
} 

void main(){
	LinkList ha;   			//定义单链表头指针			
	ha=InitList();			//初始化单链表
	CreatByRear(ha);        //尾插法创建单链表
	OutPut(ha);				//输出单链表	
	
	printf("在第2个位置上插入\n"); 
	Insert(ha,2);
	OutPut(ha);				//输出单链表	

	printf("在第2个位置上删除\n"); 
	Delete(ha,2);
	OutPut(ha);				//输出单链表	

}

运行结果如下
在这里插入图片描述

2.4.5 静态链表(自学）

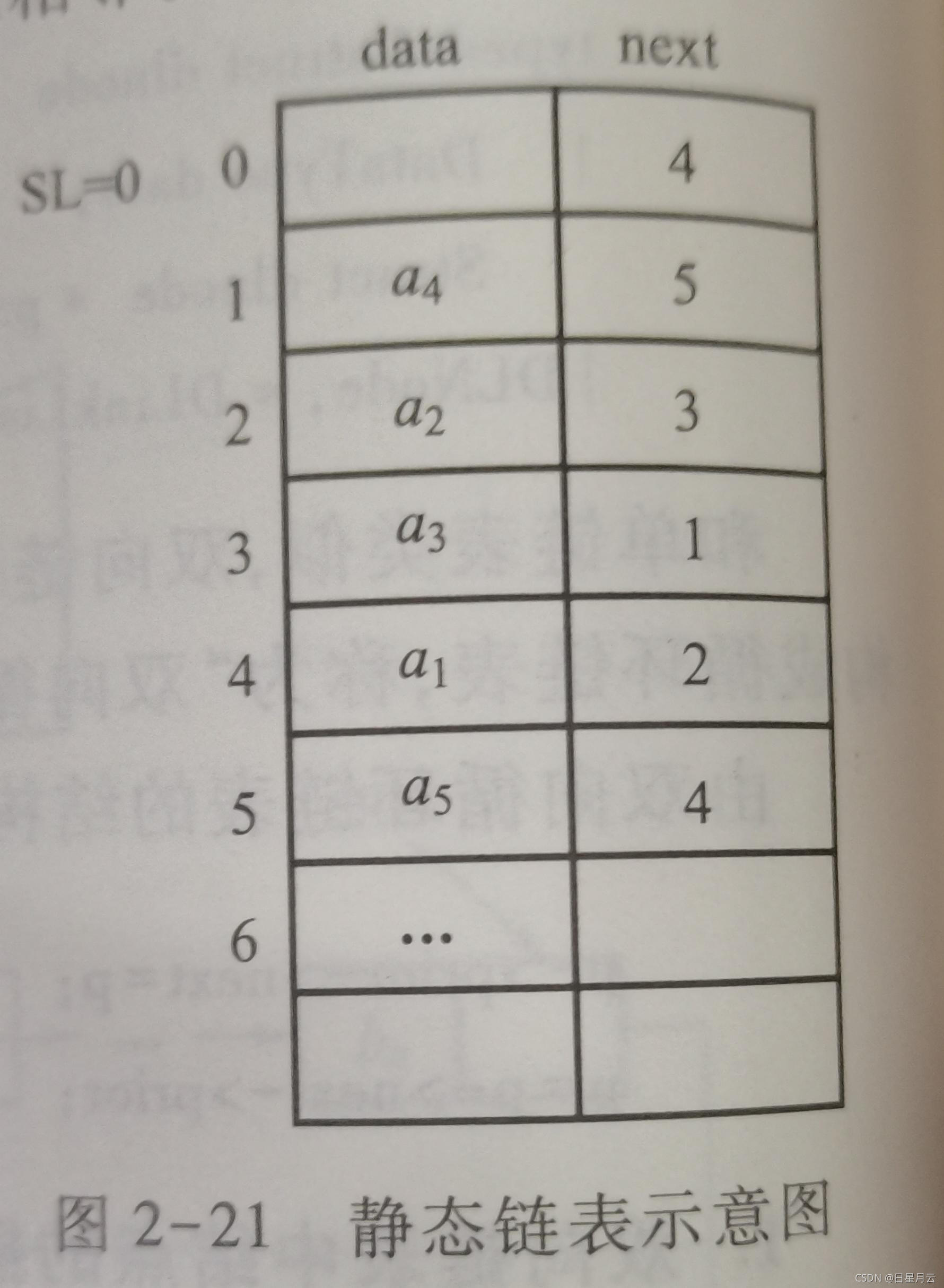
静态链表是用数组实现的，每个数据元素除了存储数据信息外,还要存储逻辑相邻的下一个数据元素在数组中的位置。可见,静态链表是用数组实现的,但是逻辑相邻的数据元素不一定在物理位置上也相邻。

图2-21所示是一个静态链表的例子,SL是一个带头结点的单链表,表示了线性表
(a1,a2,,a3,a4,a5)的存储结构。
从头结点的next域得到4,找到结点a1的位置,再从a1的next域得到2,找到a2的位置
,如此可依次访问此链表中的所有结点。
对于图2-21,最后一个结点a5的下一个元素位置为4,即a1所在的位置,
这又构成一个循环静态链表。

请添加图片描述

静态链表描述如下。  
typedef struct{
	DataType data;  
	int next;
} SNode;  //结点类型  
SNode sd[ MAXSIZE];  
int SL;  //头指针变量

这种链表的结点中也有数据域data和指针域next,与前面所讲链表中的指针不同的是,这里的指针next(整型)是结点在数组中的下标,称为“静态指针”,所以称这种链表为静态链表。通常将静态链表的next域称为“游标”(cursor),也就是用游标来模拟指针。

5-静态链表

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10 


typedef int DataType ;
typedef struct{ 
	DataType data;  
	int next;
} SNode;  //结点类型  


void Create (SNode *sd,int SL){
	int r=SL;
	SNode *s; 
	int data;
	int next=-1;
	while(next!=0){//next!=SL 即为循环 
		s=(SNode*)malloc(sizeof(SNode));
		printf("输入data：");
		scanf("%d",&data);
		printf("输入next：");
		scanf("%d",&next);	
		
		s->data=data;
		s->next=next;
		
		sd[r]=*s;
		r=s->next;
	}


} 

void CreateX (SNode *sd,int SL){
	int r=SL;
	SNode *s; 
	int data;
	int next;
	int begin=1; 
	while(next!=SL||begin==1){//next!=SL 即为循环 
		if(begin==1){
			begin=0;
		}
		s=(SNode*)malloc(sizeof(SNode));
		printf("输入data：");
		scanf("%d",&data);
		printf("输入next：");
		scanf("%d",&next);	
		
		s->data=data;
		s->next=next;
		
		sd[r]=*s;
		r=s->next;
	}


} 
void OutPutX (SNode *sd,int SL){
	SNode *s; 
	int next=SL;
	int begin=1; 

	while(next!=SL||begin==1){//next!=SL 即为循环 
		if(begin==1){
			begin=0;
		}
		*s=sd[next]; 
		printf("输出data：");
		printf("%d\n",s->data); 
		next=s->next;
	}
} 

void OutPut (SNode *sd,int SL){
	SNode *s; 
	int next=SL;

	while(next!=0){//next!=SL 即为循环 
	
		*s=sd[next]; 
		printf("输出data：");
		printf("%d\n",s->data); 
		next=s->next;
	}
} 
int main(){
	printf("非循环\n");
	SNode sd[MAXSIZE];

	int SL=4;

	sd[0].data=0;
	sd[0].next=SL;
	
	Create(sd,SL);	//2 2 3 3 1 1 5 5 4 0
	//物理位置 
	int i=0;
	for(i;i<6;i++){
		printf("%d\n",sd[i].data);
	}
	//0 5 3 1 2 4
	//逻辑位置 
	OutPut(sd,SL);//2  3  1   5   4
	
	printf("循环\n");

	SNode sdX[MAXSIZE];
	int SLX=4;

	sdX[0].data=0;
	sdX[0].next=SLX;
	CreateX(sdX,SLX);//2 2 3 3 1 1 5 5 4 4(SLX) 

	//物理位置 
	int j=0;
	for(j;j<6;j++){
		printf("%d\n",sdX[j].data);
	}
	//0 5 3 1 2 4

	//逻辑位置 
	OutPutX(sdX,SLX);//2  3  1   5   4

}

运行结果如下
在这里插入图片描述

2.5 顺序表和链表的比较

顺序表查找、遍历简单
链表插入、删除简单

2.6 实例分析与实现

约瑟夫环

一元多项式运算器

实验

约瑟夫环

约瑟夫环.c

//【算法2-16】约瑟夫环
#include<stdio.h>
#include<stdlib.h>

#define MAX 100

typedef struct NodeType{
	int id;
	int password;
	struct NodeType *next;
}NodeType; 
		 
void CreaList(NodeType**,int);//创建单问循环链表

NodeType * GetNode(int, int);//得到一个结点

void PrntList( NodeType *);//打印循环链表

int IsEmptyList( NodeType *);//测试链表是否为空

void JosephusOperate(NodeType **,int);//运行约瑟夫环问题
	 
int main(void){
	
	int n=0;
	int m=0;
	NodeType * pHead = NULL;
	do{
		//人数n超过最大人数,重新输人人数n直至满足条件为止
		if(n> MAX){ 
			printf("人数太多,请重新输入!\n");
		}
			
		printf("请输人人数n(最多%d个):",MAX);
		scanf( "%d",&n);
		
		
	}while(n > MAX);
	printf("请输入初始密码m:");
	scanf("%d", &m);
	CreaList(&pHead,n);//创建单向循环链表
	printf("\n---------打印循环链表--------\n");
	PrntList(pHead);//打印循环链表
	printf( "\n打印出队情况--\n");
	JosephusOperate(&pHead,m);//运行约瑟夫环问题  
	return 1;
}


//创建有n个结点的循环链表ppHead
void CreaList( NodeType * * ppHead, int n){
	int i=0;
	int iPassword =0;
	NodeType * pNew= NULL;
	NodeType * pCur= NULL;
	
	for(i=1;i<=n;i++){
		printf("输人第%d个人的密码:",i);
		scanf("%d", &iPassword);
		pNew = GetNode(i, iPassword);
		if (* ppHead == NULL){
			* ppHead=pCur=pNew;
			pCur->next=*ppHead;
		}
		else{ 
			pNew->next=pCur->next;
			pCur->next=pNew;
			pCur=pNew;
		}
	}
	
	printf("完成单向循环链表的创建!\n");

} 

//创建结点 
NodeType * GetNode(int id, int iPassword){//向结点中传送编号和密码
	NodeType * pNew= NULL;//建立指针
	pNew = ( NodeType * )malloc(sizeof( NodeType));//为当前结点开辟新空间
	if(!pNew){
		printf("Error, the memory is not enough!\n"); 
		exit(-1);
	}
	pNew->id=id;
	pNew->password =iPassword;
	pNew->next=NULL;//pNew的next指向空,置空表尾  
	return pNew;	
}




//依次输出至为个人,且输出密码,完成原始链表的打印 
void PrntList( NodeType * pHead){
	NodeType *pCur=pHead;
	//调用EmptyList()函数来判断f语句是否执行,若pHead为空则执行  
	if(!IsEmptyList(pHead)){
		printf("--ID-- --PASSWORD --\n");
		do{
			printf("%3d %7d\n",pCur->id,pCur->password); 
		 	pCur=pCur->next;//让指针变量pCur改为指向后继结点 
		}while (pCur!=pHead);
	}

}

int IsEmptyList( NodeType * pHead){

	if(!pHead){		
		//若pHead为空,提示“空”,返回值
		printf( " The list is empty! \n");
		return 1;
	}
	return 0;//否则返回
}



void JosephusOperate( NodeType ** ppHead, int iPassword){

	int iCounter= 0;
	int iFlag=1;
	NodeType * pPrv=NULL;
	NodeType * pCur= NULL;
	NodeType * pDel= NULL;
	pPrv= pCur=* ppHead;
	//将pPrv初始为指向尾结点,为删除做好准备
	while(pPrv->next!=*ppHead)
		pPrv = pPrv->next;
		
		
	while (iFlag){
		for (iCounter=1; iCounter < iPassword; iCounter++){		
			pPrv=pCur;
			pCur= pCur->next;
		}
	
	
		if (pPrv==pCur) iFlag=0;
		pDel= pCur;//删除pCur指向的结点,即有人出列
		
		//使得pPrv指向结点与下下一个结点相连,让pCur从链表中脱节 
		pPrv->next=pCur->next;
		//让指针pCur改为指向后继结点,后移一个结点
		pCur= pCur->next;
		iPassword =pDel->password;//记录出列的人手中的密码
		printf("第%d个人出列(密码:%d)\n",pDel->id,pDel->password);  
		free(pDel);//释放删除pDel指向的结点
	}
	*ppHead=NULL;  
	getchar();
}

运行结果如下
在这里插入图片描述

一元多项式运算器

多项式.c

#include<stdio.h>
#include<stdlib.h>
#include<string.h> 
#include<math.h>
#define DataType int
#define ERROR 0
#define TRUE 1

typedef struct node{
	float coef;//系数 
	int expn;//指数 
	struct node *next;
}LNode,*LinkList;


//【算法2-7】尾插法建立单链表 
LinkList CreatByBear(){
	LinkList H=(LinkList)malloc(sizeof(LNode)); //生成头结点 
	H->next=NULL;		//空表 
	LNode *s, *r=H;
	float c;
	int e; 
	printf("输入系数（0结束）"); 
	scanf("%f",&c);
	printf("输入指数 "); 
	scanf("%d",&e);
	while(c!=0){
		s=(LinkList)malloc(sizeof(LNode));
		s->coef=c;
		s->expn=e;
		r->next=s;
		r=s;		//r指向新的尾结点 
		printf("输入系数（0结束）"); 
		scanf("%f",&c);
		printf("输入指数 "); 
		scanf("%d",&e);
	}
	 r->next=NULL;   
	 return H;
}


//输出 

void OutPut(LinkList H){
	LNode *p=H->next;
	if (p==NULL){
		printf("0");
		return;
	}
	while(p){
		printf("%+.2fX^%d",p->coef,p->expn);
		p=p->next;
	}
	
}
double result(LinkList h,double x){
	double s=0;
	LNode *p=h->next;
	if (p==NULL){
		printf("0");
		return 0;
	}
	while(p){
		s+=p->coef*pow(x,p->expn);
		p=p->next;
	}
	return s;
} 
//相加
LinkList add(LinkList pa,LinkList pb){
	LinkList pc=(LinkList)malloc(sizeof(LNode)); //生成头结点 
	pc->next=NULL;		//空表 
	LNode *qc;
	
	LNode* qa=pa->next;
	LNode* qb=pb->next;
	LNode *headc=pc;
	
	while(qa&&qb){
		qc=(LNode*)malloc(sizeof(LNode));
		if(qa->expn<qb->expn){
			qc->coef=qa->coef;
			qc->expn=qa->expn;
			
			qa=qa->next;
		}else if(qa->expn==qb->expn){
			
			qc->expn=qa->expn;
			qc->coef=qa->coef+qb->coef;
			qa=qa->next;
			qb=qb->next;
			
		}else{
			qc->coef=pb->coef;
			qc->expn=pb->expn;
			
			qb=qb->next;
		}
		
		if(qc->coef!=0){
			qc->next=pc->next;
			pc->next=qc;
			pc=qc;	
		} else{
			free(qc);
		}
		
	}
	while(qa){
		qc=(LNode*)malloc(sizeof(LNode));
		qc->coef=qa->coef;
		qc->expn=qa->expn;
		qa=qa->next;
		qc->next=pc->next;
	
		pc->next=qc;
		pc=qc;
	}
	while(qb){
		qc=(LNode*)malloc(sizeof(LNode));
		qc->coef=qb->coef;
		qc->expn=qb->expn;
		qb=qb->next;
		qc->next=pc->next;
	
		pc->next=qc;
		pc=qc;
	}
	return headc;
} 
//相减
LinkList sub(LinkList pa,LinkList pb){
	LinkList h=pb;
	LNode *p=pb->next;
	LNode *pd;
	while(p){
		p->coef*=-1;
		
		p=p->next;
	}
	
	pd= add(pa,h);
	
	for(p=h->next;p;p=p->next){
		p->coef*=-1;
		
	}
	
	return pd;
}
//乘法
LinkList mul(LinkList pa,LinkList pb){
	LinkList H=(LinkList)malloc(sizeof(LNode)); //生成头结点 
	H->next=NULL;		//空表 
	
	LNode *as;
	LNode *bs;
	for(as=pa->next;as;as=as->next){
		LinkList h=(LinkList)malloc(sizeof(LNode));;
		h->next=NULL;
		LNode *r=h;
		for(bs=pb->next;bs;bs=bs->next){
			LNode *s=(LNode*)malloc(sizeof(LNode));
			s->coef=as->coef*bs->coef;
			s->expn=as->expn+bs->expn;
			r->next=s;
			r=s;
		}
		r->next=NULL;
		H=add(H,h);
	}
	return H;
}
//导数
LinkList der(LinkList h){
	LinkList H=(LinkList)malloc(sizeof(LNode)); //生成头结点 
	H->next=NULL;		//空表 
	LNode *r=H;
	LNode *s;

	LNode *p=h->next;
	
	while(p){
		if(p->expn!=0){
			s=(LNode*)malloc(sizeof(LNode));
			s->expn=p->expn-1;
			
			s->coef=p->coef*p->expn;
			r->next=s;
			r=s;
		}
		
		p=p->next;
	}
	
	r->next=NULL;
	return H;
} 

void main(){
	//默认指数递增排序 
	printf("输入h1\n");
	//建立 
	LinkList h1=CreatByBear();
	printf("输出h1\n");
	OutPut(h1);
	printf("\n");
	
	printf("求值\n");
	double x;
	printf("输入x：");
	scanf("%lf",&x);
	double r=result(h1,x);
	printf("%lf\n",r);


	printf("der\n");
	LinkList hder=der(h1);
	OutPut(hder);
	printf("\n");
	
	printf("输入h2\n");
	//建立 
	LinkList h2=CreatByBear();
	printf("输出h2\n");
	OutPut(h2);
	printf("\n");
	
	printf("add\n");
	LinkList hadd=add(h1,h2);
	OutPut(hadd);
	printf("\n");
//	
	printf("sub\n");
	LinkList hsub=sub(h1,h2);
	OutPut(hsub);
	printf("\n");

	printf("mul\n");
	LinkList hmul=mul(h1,h2);
	OutPut(hmul);

}

在这里插入图片描述

习题2

1.单项选择题

(1)链表不具有的特点是 ____。 B
A. 插入、删除不需要移动元素
B. 可随机访问任一元素
C. 不必事先估计存储空间
D. 所需空间与线性长度成正比

(2) 设单链表中结点的结构为(data.next)。若在指针p所指结点后插入由指针s指向的结点,则应执行____操作。 B
A.p->next=s; s->next=p;
B. s->next=p->next;p->next=s;
C.s->next=p;s=p
D. p->next=s;s->next=p->next;

(3)在双向链表指针p的指针前插入一个指针q的结点,操作是 ____。 C
注:双向链表的结点结构为(prior,data,next)。
A. p->prior=q;q->next=p;p->prior->next=q;q->prior=q;
B. p->prior=g;p->prior->next=q;q->next=p;q->prior=p->prior;
C. q->next=p;q->prior=p->prior;p->prior->next=q;p->prior=q;
D.q->prior=p->prior;q->next=q;p->prior=q;p->prior=q;

(4)对于一个具有n个结点的单链表,在已知的结点*p后插入一个新结点的时间复杂度，和在给定值为x的结点后插入一个新结点的时间复杂度分别为 ____。 B
A. O(n),O(n)
B.O(1),0(n)
C.O(1),O(1)
D.O(n),O(1)

(5)以下错误的是 ____。 A
① 静态链表既有顺序存储的优点,又有动态链表的优点。所以,它存取表中第i个元素的时间与i无关。
② 静态链表中能容纳的元素个数在表定义时就确定了,以后不能增加。

③ 静态链表与动态链表在元素的插入、删除上类似,不需做元素的移动。
A. ①②
B. ①
C. ①②③
D. ②

2.算法设计题

(1) 设有一线性表e=(e1,e2,…,e[n-1],en,其逆线性表定义为e’=(en,e[n-1],…,e2,e1)。请设计一个算法,将线性逆置,要求逆线性表仍占用原线性表的空间,并且用顺序表和单链表两种方法来表示,写出不同的处理函数。

顺序表
(1)_1.c

/*
（1）设有一线性表e=(e1,e2,...,e[n-1],en,其逆线性表定义为e'=(en,e[n-1],...,e2,e1)。
请设计一个算法,将线性逆置,
要求逆线性表仍占用原线性表的空间,
并且用顺序表和单链表两种方法来表示,写出不同的处理函数。
*/
# include <stdio.h>
# include <stdlib.h>
# include <string.h>
//函数结果状态代码 
#define TRUE 1 
#define FALSE 0
#define OK 1 
#define ERROR 0
#define INFEASIBLE -1 
#define OVERFLOW -2 


typedef int Status;
typedef int Boolean; 

#define MAXSIZE 10
typedef int ElemType;

typedef struct{
	ElemType elem[MAXSIZE];//下标从1开始，0没有值 
	int length;//线性表长度 
} SeqList; 

//1.顺序表的初始化
//【算法2-1】 顺序表的初始化
void Init(SeqList *L){
	L->length=0;

} 


//创建顺序表函数 初始化前n个数据
int CreateList(SeqList *L, int n)
{
	int i;
	if (n<0 || n>MAXSIZE) return FALSE;//n非法
	for ( i = 1; i<=n; i++)
	{
		printf("输入:"); 
		scanf("%d",&(L->elem[i]));
		L->length++;
	}
	return TRUE;
}

void Reverse(SeqList* L){
	int len=L->length+1;//数组实际长度因为有索引【0】 
	int i=1;
	for(i=1;i<=len/2;i++){
		int t=L->elem[i];
		L->elem[i]=L->elem[len-i];
		L->elem[len-i]=t;
	}
} 

void Output(SeqList* L){
	int i=1;
	for(i;i<=L->length;i++){
		printf("%d ",L->elem[i]);
	}
	printf("\n") ;
}

int main(){
	SeqList _L;
	SeqList *L=&_L;

	//初始化 
	Init(&_L);
	
	//创建 
	int n=0;
	printf("输入线性表的长度："); 
	scanf("%d",&n);
	CreateList(L,n);
	Output(L);
	
	//倒置
	Reverse(L);
	printf("倒置\n");
	Output(L);

}

运行结果如下
在这里插入图片描述

单链表
(1)_2.c

/*
（1）设有一线性表e=(e1,e2,...,e[n-1],en,其逆线性表定义为e'=(en,e[n-1],...,e2,e1)。
请设计一个算法,将线性逆置,
要求逆线性表仍占用原线性表的空间,
并且用顺序表和单链表两种方法来表示,写出不同的处理函数。
*/
#include<stdio.h>
#include<stdlib.h>
#include<string.h> 
#define DataType int
#define ERROR 0
#define TRUE 1

typedef struct node{
	DataType data;
	struct node *next;
}LNode,*LinkList;

//1.建立单链表
//尾插法建立单链表 
LinkList CreatByBear(){
	LinkList H=(LinkList)malloc(sizeof(LNode)); //生成头结点 
	H->next=NULL;		//空表 
	LNode *s, *r=H;
	int x;
	printf("输入（-1结束）"); 
	scanf("%d",&x);
	while(x!=-1){
		s=(LinkList)malloc(sizeof(LNode));
		s->data=x;
		
		r->next=s;
		r=s;		//r指向新的尾结点 
		printf("输入（-1结束）"); 
		scanf("%d",&x);
	}
	 r->next=NULL;   
	 return H;
}


// 单链表的逆置
void Reverse(LinkList H){  
	LNode * p,*q;
	p=H->next;		//p指向第一个数据结点
	H->next= NULL;		//将原链表置为空表H
	while(p){
		q=p;
		p=p->next;
		q->next=H->next;	//将当前结点插到头结点的后面(头插)
		H->next=q;
	}

} 

//遍历输出 
void OutPut(LinkList head){
	LNode *p;
	p=head->next;
	while(p){		
		printf("(%d)\n",p->data);
		p=p->next;
	}
} 


void main(){
	//建立 
	LinkList h=CreatByBear();
	OutPut(h);
	//逆置 
	Reverse(h);
	printf("逆置\n");
	OutPut(h);

}

运行结果如下
在这里插入图片描述

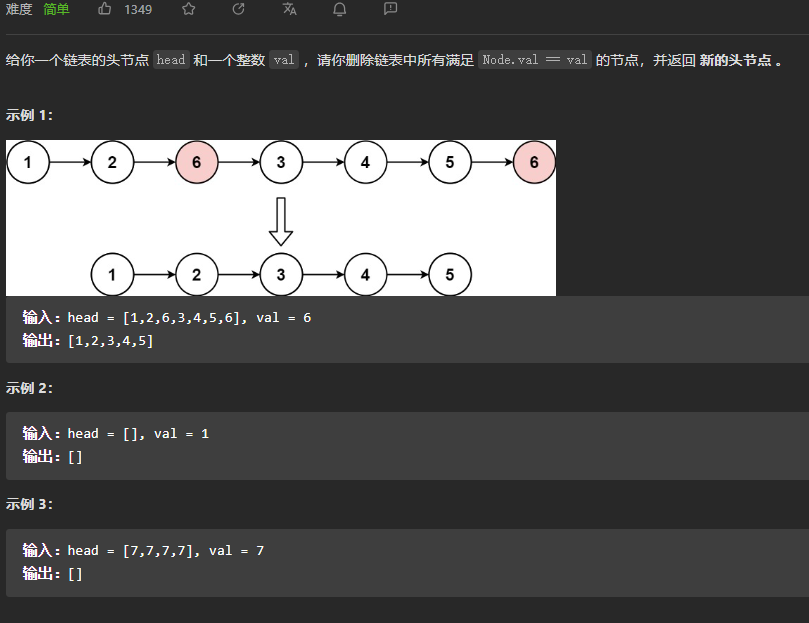
(3) 已知线性表A的长度为n,并且采用顺序存储结构。请编写算法，删除线性表中所有值为x的元素。

(3).c

/*
3）已知线性表A的长度为n,并且采用顺序存储结构。
请编写算法，删除线性表中所有值为x的元素。
*/
#include<stdio.h>

//函数结果状态代码 
#define TRUE 1 
#define FALSE 0

#define MAXSIZE 100
typedef int ElemType;

typedef struct{
	ElemType elem[MAXSIZE];//下标从1开始，0没有值 
	int length;//线性表长度 
} SeqList; 

//1.顺序表的初始化
//【算法2-1】 顺序表的初始化
void Init(SeqList *L){
	L->length=0;

} 


//创建顺序表函数 初始化前n个数据
int CreateList(SeqList *L, int n)
{
	int i;
	if (n<0 || n>MAXSIZE) return FALSE;//n非法
	for ( i = 1; i<=n; i++)
	{
		printf("输入:"); 
		scanf("%d",&(L->elem[i]));
		L->length++;
	}
	return TRUE;
}

int Delete(SeqList* L, ElemType e){
	int i=1;//存储索引 
	int find=0;//找到表值 
	for(i;i<=L->length;i++){
		if(L->elem[i]==e){
			find=1;
			break;		
		}
	
	}
	
	if(find==0){
		return 0;//删除失败 
	}
	int j;
	
	for (j=i;j<=L->length-1;j++){
		L->elem[j]=L->elem[j+1];//向上移动 
	}
	L->length--;
	return 1;//删除成功		

}

void DeleteValue(SeqList* L, ElemType e){
	int r=Delete(L,e);
	if(r==1){
		DeleteValue(L,e);
	}
	
}

void Output(SeqList* L){
	if(L->length==0){
		printf("无");  
	} 
	int i=1;
	for(i;i<=L->length;i++){
		printf("%d ",L->elem[i]);
	}
	printf("\n") ;
}

int main(){
	SeqList _L;
	SeqList *L=&_L;

	//初始化 
	Init(&_L);
	
	//创建 
	int n=0;
	printf("输入线性表的长度："); 
	scanf("%d",&n);
	CreateList(L,n);
	Output(L);
	
	//删出所有的给定值
	int x;
	printf("输入删除的值：");
	scanf("%d",&x); 
	DeleteValue(L,x); 
	Output(L);
}

运行结果如下
在这里插入图片描述

(5) 假设有一个循环链表的长度大于1,且表中既无头结点也无头指针。已知s为指向链表中某结点的指针，试编写算法,在链表中删除指针s所指结点的前驱结点。

/*
（5）假设有一个循环链表的长度大于1,且表中既无头结点也无头指针。
已知s为指向链表中某结点的指针，
试编写算法,在链表中删除指针s所指结点的前驱结点。
*/
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct node{				//链表结点结构体定义 
	int number;			//数字 
	struct node *next;	//*next的类型是指向本结构体类型的指针 
	
}Node,*LinkList; 

void Delete(Node*s){
	Node* q=s;
	while(q->next->next!=s){
		q=q->next;
	}
	Node* p=q->next;//此时q为s的 前驱结点p 的前驱结点
	q->next=s;//删除 
	free(p); //释放 
	 
} 
void main(){
	int n;
	printf("输入结点个数"); 
	scanf("%d",&n);
	int i;
	//构建循环链表
	//0->1->2->...->n-1->0 
	Node* s[n];
//	for(i=0;i<n;i++){
//		s[i]=NULL;					
//	}
	for(i=0;i<n;i++){
		s[i]=(Node*)malloc(sizeof(Node));	
		s[i]->number=i;				
	}
	for(i=0;i<n;i++){
		if(i==n-1){
			s[i]->next=s[0];
		}else{
			s[i]->next=s[i+1];
		}					
	}
	
	//输出 
	for(i=0;i<n;i++){
		printf("%d\t",s[i]->number);
	}
	printf("\n");
	//验证输出
	printf("%d",s[4]->next->number); 
	printf("\n");
	
	//删除s[3]的前驱结点
	//s[2] 
	Delete(s[3]);
	
	//输出 
	for(i=0;i<n;i++){
		if(i==2){
			;
		}else{
			printf("%d\t",s[i]->number);
		}
		
	}
	printf("\n");
	//验证
	LinkList h=s[0];
	Node *p=h->next; 
	while(p!=h){
		printf("%d\t",p->number);
		p=p->next;
	} 
}

运行结果
在这里插入图片描述

(8)设指针la和lb分别指向两个无头结点单链表中的首元结点,试设计算法,从表la中删除自第i个元素起共len个元素,并将它们插入表lb的第j个元素之后。

8.c

#include<stdio.h>
#include<stdlib.h>
#include<string.h> 
#define DataType int
#define ERROR 0
#define TRUE 1

typedef struct node{
	DataType data;
	struct node *next;
}LNode,*LinkList;

//1.建立单链表

//【算法2-7】尾插法建立单链表 
LinkList CreatByBear(){

	LinkList H=NULL;	//无头结点 
	
	LNode *s, *r;
	int x;
	printf("输入（-1结束）"); 
	scanf("%d",&x);
	while(x!=-1){
		s=(LinkList)malloc(sizeof(LNode));
		s->data=x;
		if(H==NULL){
			H=s;
			r=H;
		}else{
			
			r->next=s;
		}
		r=s;		//r指向新的尾结点 
		printf("输入（-1结束）"); 
		scanf("%d",&x);
	}
	 r->next=NULL;   
	 return H;
}
//遍历输出 
void OutPut(LinkList head){
	if(head==NULL){
		printf("NULL");
		return ;
	}
	LNode *p;
	p=head;
	while(p){		
		printf("(%d)\n",p->data);
		p=p->next;
	}
} 
//2.求表长
//【算法2-8】 求单链表的表长
int Length(LinkList H){
	LNode *p=H;   //p指向头结点
	int j=0;
	while(p!=NULL)  {
		p=p->next;
		j++;
	} 
	return j;
} 

LinkList Get(LinkList H,int k){
	LNode *p=H;
	int j=1;
	while(p!=NULL&&j<k){
		p=p->next;
		j++;
	}

	if(j==k )return p;
	else return NULL;
	
}

//算法 
int Fun(LinkList la,LinkList lb,int i,int len,int j,LinkList *an){
	
	
	LNode *b=Get(lb,j);  //查找第j个结点
	if(b==NULL){
		printf("插入位置j错") ;
		return ERROR; 
	}
	
	LNode *b_=b->next;  //保存原来b后面的结点 
	
	if(i==1){
		if(len>Length(la)){
			printf("删除长度len错") ;
			return ERROR; 
		}
		LinkList tem=la;
		la=NULL; 
		LNode *a=Get(tem,len);
		
		*an=a->next;
		
		a->next=NULL;
		b->next=tem;
		a->next=b_;
		
		la=*an;
	
		return TRUE;
	}
	LNode *a=Get(la,i-1);  //查找第i-1个结点

	
	if(a->next==NULL) {   //第i个结点不存在，不能删除 
		printf("删除位置i错") ;
		return ERROR; 
	} 
	
	if(i-1+len>Length(la)){
		printf("删除长度len错") ;
		return ERROR; 
	} 
	
	 
	int count=0;
	for(count=0;count<len;count++){
			 
	
		LNode *s=a->next;//第i个结点 
		a->next=s->next;//删除 
		
		b->next=s;//新结点插入 第j结点 后 
		b=s;	//尾插 
	
		
	}

	b->next=b_; 

	return TRUE;

}





void main(){
	printf("输入la:\n");
	//建立 
	LinkList la=CreatByBear();
	OutPut(la);

	//建立 
 	printf("\n输入lb:\n");
	LinkList lb=CreatByBear();
	OutPut(lb);
	
	int i;
	int len;
	int j;
	printf("输入i:");
	scanf("%d",&i); 
	while(i<=0){
		printf("重新输入i:");
		scanf("%d",&i);
	}
	
	printf("输入len:");
	scanf("%d",&len);
	while(len<=0){
		printf("重新输入len:");
		scanf("%d",&len);
	}
	
	printf("输入j:");
	scanf("%d",&j);
	while(j<=0){
		printf("重新输入j:");
		scanf("%d",&j);
	}
	printf("\n");	
	LinkList *an=(LinkList*)malloc(sizeof(LinkList));	
	int result=Fun(la,lb,i,len,j,an);
	if(result==1){
		printf("输出la:\n");
		if(i==1){
			la=*an;			
		}
		
		OutPut(la);
		
		printf("\n输出lb:\n");
		OutPut(lb);
	}
	
}

运行结果如下
在这里插入图片描述

(9)设带头结点的线性单链表A=(a1,a2,…,am),B=(b1,b2,…bn)。试编写算法按下列规则合并A、B为线性单链表C,使得

C=(a1,b1,…,am,bm,b_(m+1),…,bn),m<=n
或者
C=(b1,a1,…,bn,an,a_(n+1),…,am),m>n

9.c
function1和function2都可以用

#include<stdio.h>
#include<stdlib.h>
#include<string.h> 
#define DataType int
#define ERROR 0
#define TRUE 1

typedef struct node{
	DataType data;
	struct node *next;
}LNode,*LinkList;

//1.建立单链表

//【算法2-7】尾插法建立单链表 
LinkList CreatByBear(){
	LinkList H=(LinkList)malloc(sizeof(LNode)); //生成头结点 
	H->next=NULL;		//空表 
	LNode *s, *r=H;
	int x;
	printf("输入（-1结束）"); 
	scanf("%d",&x);
	while(x!=-1){
		s=(LinkList)malloc(sizeof(LNode));
		s->data=x;
		
		r->next=s;
		r=s;		//r指向新的尾结点 
		printf("输入（-1结束）"); 
		scanf("%d",&x);
	}
	 r->next=NULL;   
	 return H;
}
//2.求表长
//【算法2-8】 求单链表的表长
int Length(LinkList H){
	LNode *p=H;   //p指向头结点
	int j=0;
	while(p->next!=NULL)  {
		p=p->next;
		j++;
	} 
	return j;
} 

//3.查找操作 
//(1) 按序号查找  Get(H,k)
//【算法2-9】单链中按序号查找 
LinkList Get(LinkList H,int k){
	LNode *p=H;
	int j=0;
	while(p->next!=NULL&&j<k){
		p=p->next;
		j++;
	}

	if(j==k )return p;
	else return NULL;
	
}



//遍历输出 
void OutPut(LinkList head){
	if(head==NULL){
		printf("NULL");
		return;
	}
	LNode *p;

	p=head->next;
	
	while(p){		
		printf("(%d)\n",p->data);
		p=p->next;
	}
} 


LinkList function(LinkList A,LinkList B){
	LinkList C = (LinkList)malloc(sizeof(LNode));
    C->next = NULL;

	LinkList pa, pb, qa, qb;
    pa = A->next;  // pa 指向 A 的首元结点
    pb = B->next;
    C = A;        // 因为 C 中第一个元素是 A 中的元素，所以只需要 C 指向 A就行了
    while(pa && pb)
    {
        qa = pa;
        qb = pb;
        pa = pa->next;
        pb = pb->next;
        qb->next = qa->next;
        qa->next = qb;
    }
    if(!pa)  // 如果 A 链表的长度小于 B 链表的长度//默认小于等于 
        qb->next = pb; // 将 B 的后续节点连接到新链表的尾端
    pb = B;  // 准备删除 B 链表
    free(pb);
 
    return C;
}


LinkList function2(LinkList l,LinkList sh){
	LinkList H=(LinkList)malloc(sizeof(LNode)); //生成头结点 
	H->next=NULL;		//空表 
	LNode *s, *r=H;
	LNode *ls=l->next;
	LNode *ss=sh->next;
	
	int i;
	int n=Length(sh);
	
	for(i=0;i<2*n;i++){
		if(i%2==0){//插sh 
			s=ss;
			
			r->next=s;
			r=s;
			
			ss=ss->next;
		}else{
			s=ls;
			
			r->next=s;
			r=s;
			
			ls=ls->next;
		}
	
	}
	
	r->next=ls;
 
	
	return H;
}
void main(){
	//建立 
	printf("a\n");
	LinkList a=CreatByBear();
	OutPut(a);
	
	printf("\nb\n");
	LinkList b=CreatByBear();
	OutPut(b);
	LinkList c;
	printf("\n");
//	if(Length(a)<=Length(b)){
//		c=function(a,b);
//	}else{
//		c=function(b,a);
//
//	}		

	if(Length(a)>Length(b)){
		c=function2(a,b);
	}else{
		c=function2(b,a);

	}
	printf("c\n");
	OutPut(c);

}