1简介

MPU9250是一款9轴运动跟踪装置，在它3x3x1mm的封装中集成了3轴陀螺仪，3轴加速度计，3轴磁力计以及运动处理器（DMP）并且兼容 MPU6515。通过IIC，可以直接输出9轴的全部数据。因此它也是四轴姿态结算的基础，所以能够正确获取MPU9250的数据是十分重要的。这个芯片也为兼容其他传感器开放了辅助IIC接口，比如压力传感器。也就是所谓的10轴

MPU9250具有三个16位加速度AD输出，三个16位陀螺仪AD输出，三个6位磁力计AD输出。提供可编程陀螺仪参数选择（±250，±500,±1000,and±2000°/s(dps)），可编程加速度参数选择**(±2g,±4g,±8g,±16g)**。该装置提供IIC和SPI的接口，2.4-3.6v的供电电压，还有单独的数字IO口，支持1.7V到VDD。通信采用400KHz的IIC和1MHz的SPI，若需要更快的速度，可以用SPI在20MHz的模式下直接读取传感器和中断寄存器。

2 原理

2.1 加速度计

加速度计顾名思义是测量物体的加速度
引入一个模型

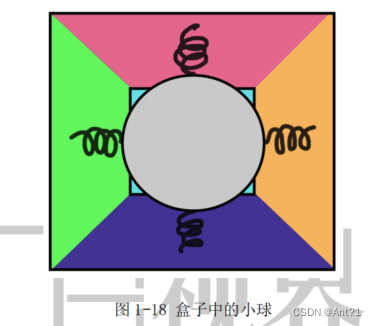
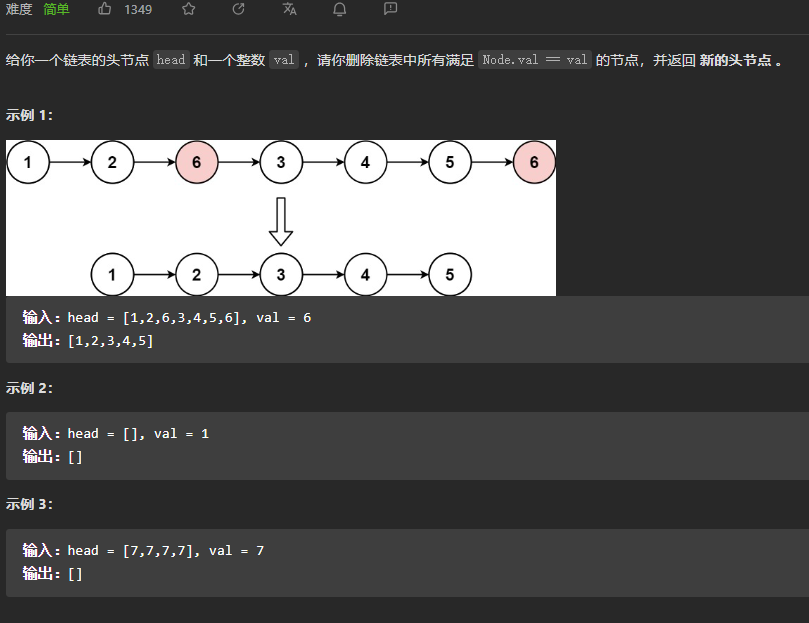
我们假设这里有一架四轴飞行器悬停在空中，而且在飞行器上固定了一个正方体的盒子。这个
盒子中有一个无重量的小球（在计算时可以不受重力的影响），它的对应盒子的
6 个面都被弹簧正好抵着（此时弹簧形变为 0）
此时我们让飞行器突然往左飞一下。那么能很明显的发现球会向右边的墙压
一点儿过去。

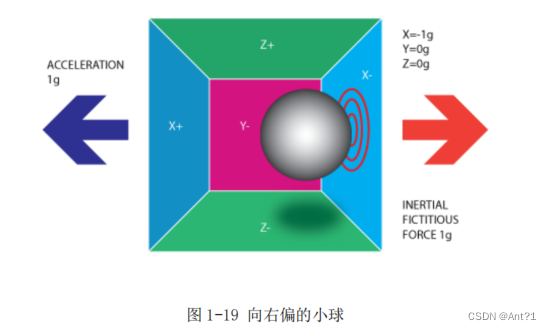
这种力我们称之为惯性力（其实是没有惯性力这种力的，我们也可以称之为假象力

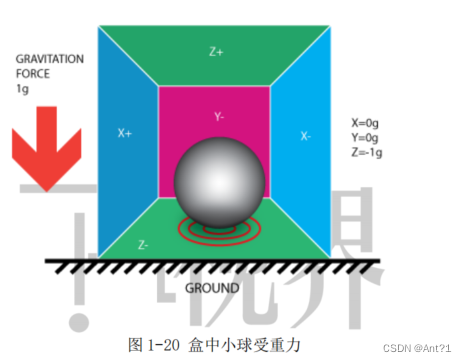
只要是在地球上运动的物体，在计算的时候还有个力是不可忽略的，所以我
们无论在哪都需要考虑进去，这个力就是重力。如图 1-20 所示，此时的小球有
重量了。那么，我们的传感器也迅速测出了 X=0g Y=0g Z=-1g 的数值。

如果以地球为参考系的话，就并不是有加速度就说明物体是在运动的。他此
时相对地球静止。那么我们此时让飞行器顺时针倾斜 45°看看会怎么样？如图
1-21 所示：

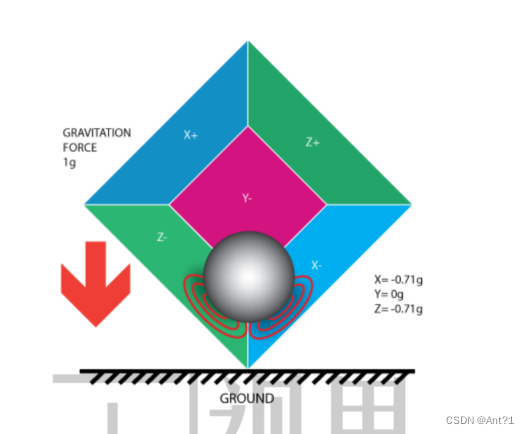
注意，此时小球并未与 Y 平面发生接触，我们可以从加速度计中读取到：
X=-0.71g Y=0g Z=-0.71g，此时飞行器是静止的，小球也是静止的，X 和 Z 方向
上的力把重力加速度分担开来了。加速度既是瞬时力，得到的加速度的值又能干
什么用呢？我们再来看
在上面的基础上此时把倾斜的飞行器前后方向倾斜 45°。得到如图 1-22 所
示，此时小球对我们模型的三个面都有相同的压力了

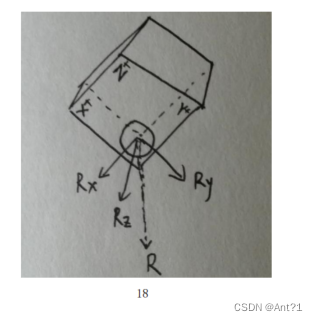
我们把这个模型受力换成直观的空间坐标图 1-23，原点即为小球中心点。
Rx，Ry 与 Rz 分别对应上图中的 Rx，Ry 与 Rz。R 为小球所受重力，也是 Rx，Ry
和 Rz 的合力。

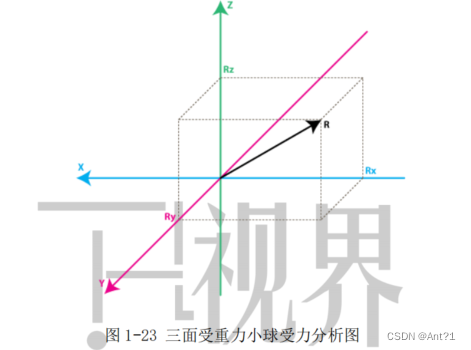
现在应该知道获得的加速度的力是用来计算什么的吧。没错，就是角度！
比如加速度计读到：（注意这里，为了计算出不同角度假设这里小球不再是
均匀的与三面受力，这里我们用模拟型传感器来举例，MPU9250 是数字型传感器，
但是原理相通）
RX=2.00V
RY=1.50V
RZ=0.75V
然后我们还需要减去加速度的偏移量才能得到实际的值，偏移量的大小是根
据芯片所处不同情况（温度、气压、材料、位置等）而产生的不同误差来决定的。
假设加速度计三轴的偏移量都是 0.50V（这里只是假设，真实值正常情况下可能
没有这么大偏移），此时可以得到：
RX=2.00V-0.50V=1.50V
RY=1.50V-0.50V=1.00V
RZ=0.75V-0.50V=0.25V
我们最终要得到是加速度的单位所以还需要把加速度的电压值转换成加速
度，这个值在芯片的加速度寄存器配置手册里面有写，配置的不同计算的数值不
同，那么此处为了方便计算假设传感器被设置的灵敏度为 0.5V/g，
此时便可得到：
RX=1.50V/0.5V/g=3g
RY=1.00V/0.5V/g=2g
RZ=0.25V/0.5V/g=0.5g
因此，就可以根据最初的公式 R
得到合力 R 的值为 3.64g。

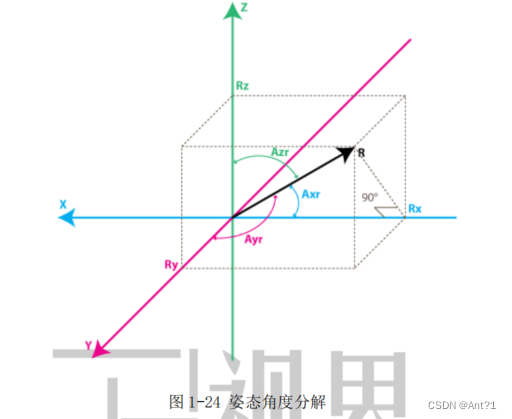
知道三角形两个边的数值了，那么此时姿态的角度的值根据三角函数也可以
很容易计算出来：
cos∠xr=（RX/R）=0.824
cos∠yr=（Ry/R）=0.549
cos∠zr=（Rz/R）=0.137
然后计算反三角函数得到角度：
∠xr=arccos（RX/R）=34.5°
∠yr=arccos（Ry/R）=56.7°
∠zr=arccos（Rz/R）=82.12°
过R做RX的垂线垂足交予RX的绝对值
此时，芯片此时姿态方向与每个轴的夹角度数就都知道了，这就是芯片的瞬时姿态。

2.2陀螺仪

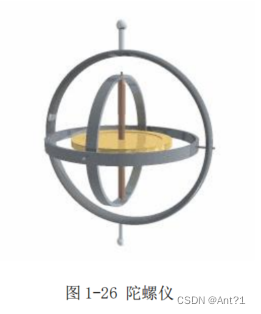
仔细观察陀螺仪的结构就不难发现陀螺仪在三个相互垂直的方向各有一根横梁。中间那根黄色的杆决定了黄色转子是围绕着它做高速旋转运动。这里面每一根杆都允许他所承载的载体在这个方向上做正反 360°旋转。而这三根杆刚好反映出了中心转子在 x 轴和 y 轴 z 轴方向上分别旋转的角度。就好像我们的芯片
分别围绕自身 x 轴，y 轴和 z 轴旋转的角度。

其实对于陀螺仪传感器我们还可以再分解成单轴，就像加速度分解成弹簧秤
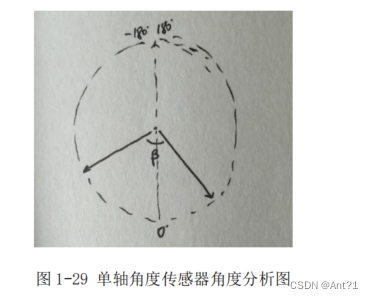
一样。分解出来最相近的也就是图 1-28 所示的单轴角度传感器。

单轴角度传感器是纪录传感器在一个单轴的角度倾斜的表现。也就是我们之前 XYZ 三轴，任取一轴做测量。比如图 1-29 所示，假如绕 x 轴旋转的话，就可以记录出传感器在绕 x 轴在-180°~+180°的角度的单独变化。

之前讲的传统陀螺仪其实主要是利用角动量守恒的原理，它是一个不停转动
的物体，它的转轴指向不随承载它的支架的旋转而变化。但是 MEMS 陀螺仪
（gyroscope）的不可能也这么设计，因为要用微机械技术在硅片衬底上加工出
一个可转动的结构可不是一件容易的事。所以工程师们在 MEMS 陀螺仪中利用的
科里奥利力（旋转物体在有径向运动时所受到的切向力）。简单科普一下科里奥
利力：

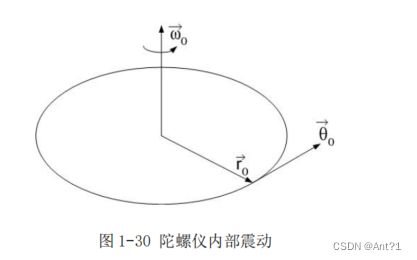
在空间设立动态坐标系（见图 1-30）。通过方程计算加速度可以得到三项速度值，分别来自径向加速、科里奥利加速度和向心加速度

假设我们此时在圆盘上放置一个小块，如图 1-31 所示。科里奥利力产生的条件就是物体在圆盘上做径向运动。因此，在 MEMS 陀螺仪的设计上，当这个物体被驱动，不停地来回做径向运动或者震荡，与此对应的科里奥利力就会不停地在横向来回变化，并有可能使物体在横向作微小震荡，相位正好与驱动力差 90度。（如图 1-31 所示）

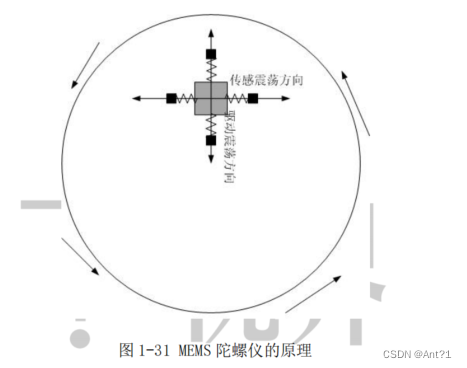
由于 MEMS 陀螺仪内部有两个方向的可移动电容板。通过径向的电容板加震荡电压迫使物体作径向运动（有点像加速度计传感器中的自测试模式），横向的电容板用来测量由于横向科里奥利运动带来的电容变化。**因为科里奥利力正比于角速度，所以我们可以由电容的变化来计算出角速度。**A3 交变科里奥利力在陀螺仪中的使用。

陀螺仪并不是测量角度的，而是测量角度变化量的传感器，也就是角速度。

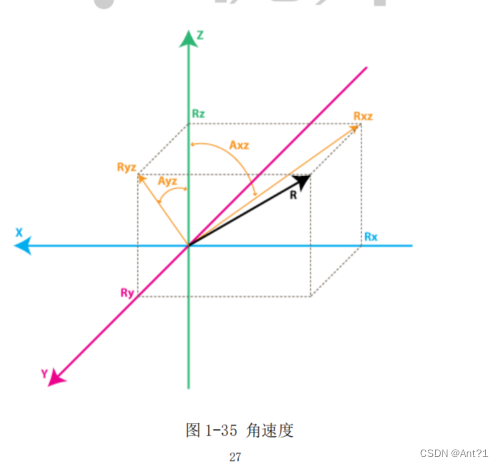
Rxz旋转Axz角度到Z轴（绕y轴旋转） Ryz旋转Ayz角度到Z轴（绕z轴旋转）
我们现在给这个模型加上两个角度。也就是图中的∠xz 和∠yz，此处 Rxz是惯性力矢量 R 在 XZ 平面上的投影 Ryz 是惯性力矢量 R 在 YZ 平面的上投影。此时，我们让这个模型（R）围绕 x 轴做逆时针旋转，然后（R）再围绕着 y 轴做逆时针旋转。从陀螺仪中可以得到（为了方便计算我们此处都用简单的数值，还是以模拟电压型传感器做例子）：
∠xz 速率 = 2.00V
∠yz 速率 = 0.50V
和加速度一样，陀螺仪也有偏移量，所以在这里也减去陀螺仪的偏移量。比
如这里是 1.00V，那么可以得到较真实电压数据：
∠xz 速率 = 2.00V-1.00V=1.00V
∠yz 速率 = 0.50V-1.00V=-0.50V
然后再根据陀螺仪的灵敏度转化为角速率，比如设置的陀螺仪的灵敏度是
0.1V/deg/s那么我们现在就可以得到：
∠xz 速率 = 1.00V/0.1V/deg/s=10°/s
∠yz 速率 = -0.50V/0.1V/deg/s=-5°/s
所以陀螺仪算出的数据就是角速度。这就可以解决了上一章快速转动无法得到平滑姿态的问题。那么∠yz 速率怎么会有带负号？举个例子，当一架飞行器在一秒钟内顺时针旋转 360°时，会测出来 360°/s。那么逆时针旋转自然就是-360°/s 了，所以-5°/s 就是逆时针的角速率了。

2.3磁力计

1.从地理课本中我们知道地球磁场的极点和地理的极点之间并不重合，他们之间有着大概 11°左右的偏差。
2.地磁和地理位置的关系刚好是相反的。也就是说地理南极附近的是地磁北
极（N），地理北极附近的是地磁南极（S）。现在的电子罗盘和以前的指南针的原理也大不一样。地球磁场的强度只有0.4-0.6Gauss，这其实是非常非常微弱的磁场。比手机内部扬声器工作时产生的磁场还小，所以电子设备的抗干扰还是一门技术活啊。而磁场传感器芯片需要探知的就是这个微小强度磁场。

我们以 LSM303 为例子来讲解一下磁力计的内部构造。LSM303 是一块磁力计的传感器。以前没有九轴传感器这样集成的芯片的时候，通常的做法是，姿态电路板上是六轴传感器再单独加上磁力计或者加上气压芯片。其实 MPU9250 也是这样的，只是在 MU6050 的基础上增加了一个磁力传感器罢了。LSM303 这种磁力计，里面还自带了加速度计。

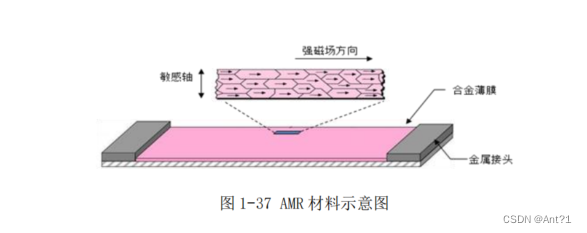
LSM303DLH 中磁力计采用各向异性磁致电阻材料来检测空间中磁感应强度的大小。这种具有晶体结构的合金材料对外界的磁场很敏感，磁场的强弱变化会导致 AMR 自身电阻值发生变化。在制造过程中，将一个强磁场加在 AMR 上使其在某一方向上磁化，建立起一个主磁域，与主磁域垂直的轴被称为该 AMR 的敏感轴，
如图 1-37 所示。

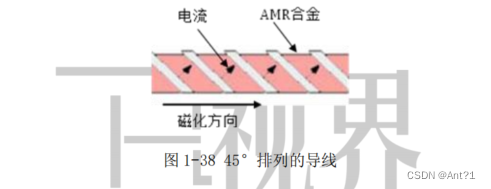
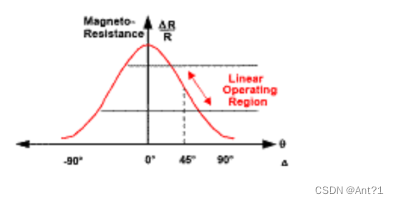
为了使测量结果以线性的方式变化，AMR 材料上的金属导线呈 45º角倾斜排列，电流从这些导线上流过，如图 1-38 所示。由初始的强磁场在 AMR 材料上建立起来的主磁域和电流的方向有 45º的夹角。

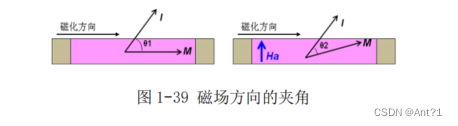
当有外界磁场 Ha 时，AMR 上主磁域方向就会发生变化而不再是初始的方向了，那么磁场方向和电流的夹角θ也会发生变化，如图 1-39 所示。

对于 AMR 材料来说，θ角的变化会引起 AMR 自身阻值的变化，并且呈线性关
系，如图 1-40 所示。

ST 则是利用惠斯通电桥检测 AMR 阻值的变化，如图 1-41 所示，R1/R2/R3/R4是初始状态相同的 AMR 电阻，但是 R1/R2 和 R3/R4 具有相反的磁化特性。

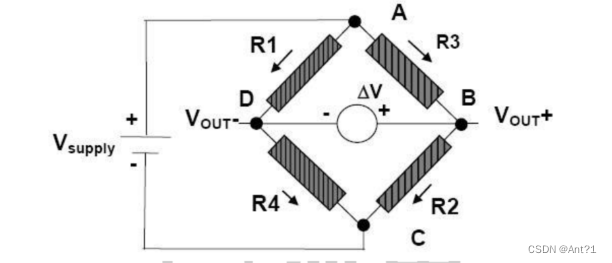
当检测到外界磁场的时候，R1/R2 阻值增加∆R 而 R3/R4 减少∆R。这样在没
有外界磁场的情况下，电桥的输出为零；而在有外界磁场时电桥的输出为一个微
小的电压∆V。当 R1=R2=R3=R4=R，在外界磁场的作用下电阻变化为∆R 时，电桥
输出∆V 正比于∆R。所以就根据电压的大小来判定磁场的大小

当然在使用磁力计传感器的时候，也是要做校准的。举个例子，水平放置磁
力计，我们可以得到数值：（为方便计算，此处也是假设数值）
X=233（和之前一样都是电压转换的对应值比如：2.3V 对应 233）
Y=248
Z=156
因为这个数值是带有磁场干扰的数值，所以我们必须要减去相应的偏移量。如图 1-45 所示可以看到我们现在测得圆心在 C（Xn，Yn）。但是不管我们怎么样，偏移量是差不多的。所以，我们测得的圆心 C 就是本地的偏移量。减去这个偏移量的一个办法就是在接下来测得的数据中直接减去这个圆心的数值。

将磁力计平放在桌子上，只需将传感器水平旋转一圈，就可以测量 Xy 轴的
数据（水平方向为磁力计的 Xy 轴）。此时的数据就会像图中那样形成一个圆一
样。比如我们此时得到 x 轴的值是 0.5V~2.7V 之间的数据，也就是对应数值为
50~270，那么此时只需要将最小值和最大值相加再除以 2，就可以得到偏移圆的
圆心坐标，即：
（50+270）/2=160=Xn
同理也可以得到 y 轴，假如是 Yn=120.再将之前得到的数据直接减去这个偏
移的值，就可以得到真正圆的圆心位置，即：
X=233-160=73
Y=248-120=128
因为磁力计此时是水平的，所以也可以得到方位角（指南针功能）：∠方位角=arctan（Y/X）=arctan（128/73）=60.255°至于西偏南还是东偏南还是什么的就取决于每个传感器具体的规定了。不过既然角度都已经知道了，那么方向也很好确定了。
z 轴的偏移值的计算要绕 x 轴旋转 90°（此时 z 轴水平），然后也是同样远离可以得到最大最小值，相加除 2 即可得到偏移数值。

文章引用《姿态传感器开发入门手册：基于 MPU9250范旭阳 编著》 如有侵权立删除