一、hash_table的介绍

hash_table可提供对任何键值对的存取和删除操作。由于操作对象是键值对，所以hash table也可被视为一种字典结构(dictionary)。这种结构的用意在于提供常数时间的基本操作，就像stack或queue那样。乍听之下这几乎是不可能的任务，因为约束制条件如此之少，而随着元素个数增加，搜寻操作必定耗费更多时间。

二、问题

举个例子，这里有一些元素，都是16-bits且不带正负号的整数，范围0-65535，如何存储这些整数，并快速的查找呢？
我们用一个array就可以满足上述期望。 首先配置一个array A，它拥有65536个元素，索引号码0-65535，初值全部为0，如下图5-21，每一个元素值代表相应元素的出现次数。如果插入元素i,我们就执行A[i]++,如果删除元素i，我们就执行A[i]--,如果搜寻元素i,我们就检查A[i]是否为0。以上的每一个操作都是常数时间.这种解法的额外负担的是array的空间和初始化时间。

三、分析

这个解法存在两个问题：

第一，如果元素是32-bits，而非16-bits,我们所准备的array A的大小就必须是2的32次方=4GB,这就大得不切实际了。

第二，如果元素型态是字符串而非整数，将无法被拿来作为array的索引。

第二个问题不难解决。就像数值1234是由阿拉伯数字1,2,3,4构成一样，字符串"jhou”是由字符·j',‘j',h','o,'u'构成。那么，既然数值1234是1*103+2*102+3*101+4*10°，我们也可以把字符编码，每个字符以一个7-bits数值来表示（也就是ASCII编码），从而将字符串"jjhou·表现为：
'j*128+·j1*1283+"h'*1282+"0'*1281+·u'*1280。于是先前的array实现法就可适用于“元素型别为字符串”的情况了。但这并不实用，因为这会产生出非常巨大的数值."jhou·的案引值将是：
106*1284+106*1283+104*1282+111*1282+117*128°=28678174709。这太不切合实际了。更长的字符串会导致更大的索引值！

这就回归到第一个问题：array的大小。如何避免使用一个大得荒谬的array呢？办法之一就是使用某种映射函数，将大数映射为小数。负责将某一元素映射为一个“大小可接受之索引”，这样的函数称为hash function(散列函数)。

例如，假设X是任意整数，Tablesize是array大小，则X%Tablesize会得到一个整数，范围在0-Tablesize-1之间，正好作为表格（也就是array)的索引，使用散列函数会带来一个问题：可能有不同的元素被映射到相同的位置(即有相同的索引)。这无法避免，因为元素个数大于array容量，这便是所谓的“碰撞(collision)”问题。解决碰撞问题的方法有许多种，包括线性探测(linear probing）、二次探测(quadratic probing)、开链(separate chaining)…等做法。

四、线性探测(linear probing)

当hash function计算出某个元素的插人位置，而该位置上的空间已不再可用时，我们应该怎么办？

最简单的办法依次向后探测，直到寻找到下一个空位置为止。（如果到达尾端，就绕到头部继续寻找)。只要表格（亦即array)足够大，总是能够找到一个安身立命的空间，但是要花多少时间就很难说了，进行元素搜寻操作时，道理也相同，如果hash function计算出来的位置上的元素值与我们的搜寻目标不符，就循序往下一一寻找，直到找到吻合者，或直到遇上空格元素。

 五、二次探测(quadratic probing)

二次探测法是指采用前后跳跃方式探测的方法，发生冲突时，向后 1 位探测，向前 1 位探测，向后 4 位探测，向前 4 位探测......以跳跃式探测，避免堆积。

二次探测的增量序列为 d=1，-1,4，-4,9，-9，16，-16，，，

若当前扫描的元素的地址已经有元素了，那么，当前元素就保存在该地址的后移偏量。

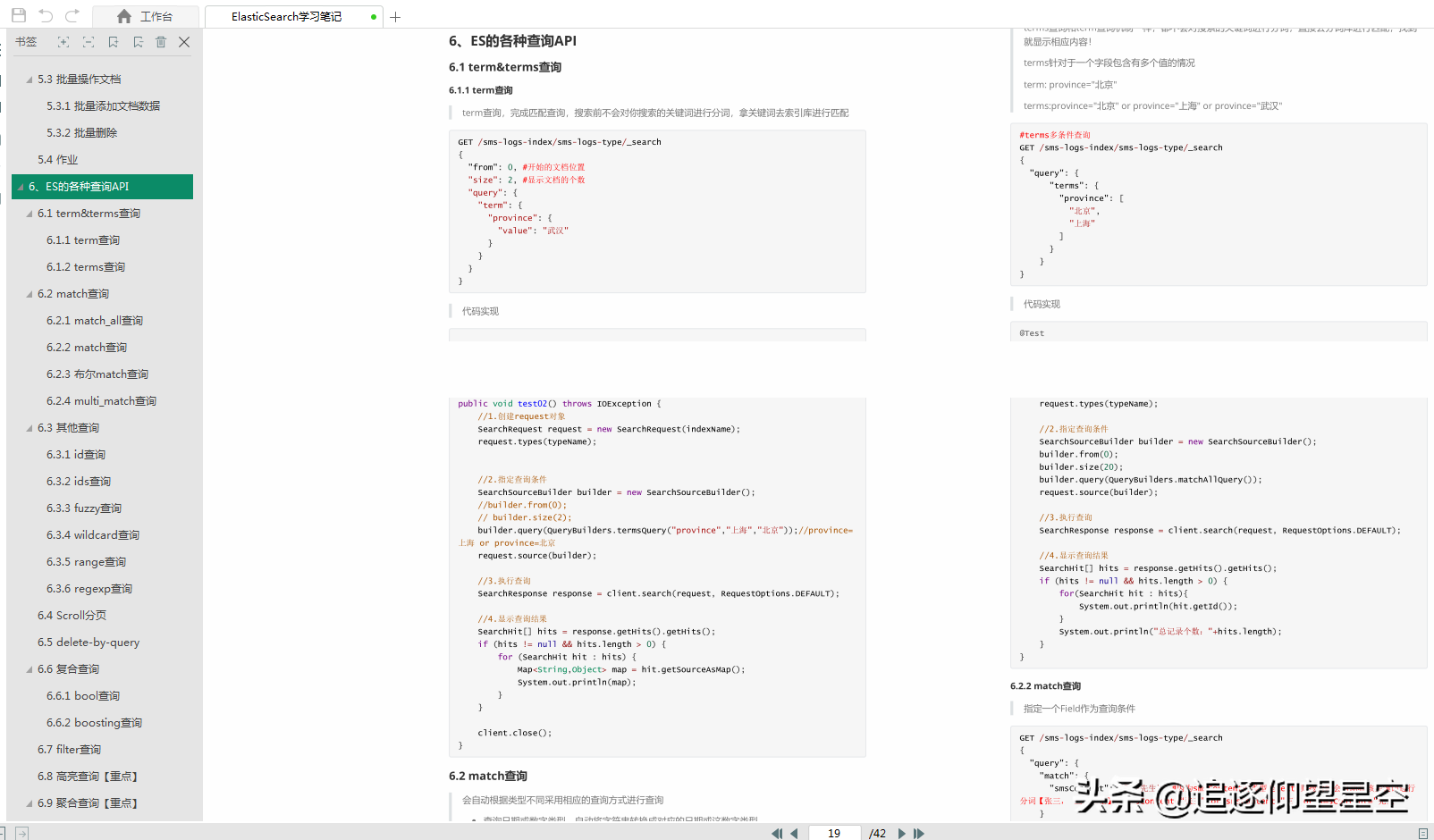
举个例子：有数组{47, 7, 29, 11, 16, 92, 22, 8, 3} ，接下来我们将所有元素对11取余，如下图所示。

 首先创建一个散列表，现在根据取余的值将元素放入散列表，如下图所示。

 其中47,7,11,16,92这些元素是根据取余的值直接放入散列表的。而29取余的值为7,7的位置上已经有元素了，那么我们放在7+1^2的位置上。3取余的值是3,3的位置上也已经有元素了，那么我们看3+1^2上也有元素，再看3-1^2的位置上没有元素，那么我们现在就放在这里。那么其他元素也是一样的道理。

 六、开链(separate chaining)

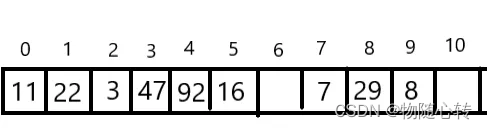
另一种与二次探测法分庭抗礼的，是所谓的开链(separate chaining)法。这种做法是在每一个表格元素中维护一个list。散列函数为我们分配某一个list,然后我们在那个list身上执行元素的插入，搜寻、删除等操作.虽然针对list而进行的搜寻只能是一种线性操作，但如果list够短，速度还是够快的

 

 

参考：

ixaC++ STL中哈希表 hash_map从头到尾详细介绍_yousss的博客-CSDN博客_std::hash_maph

线性探测-闭散列_小羊教你来编程的博客-CSDN博客_线性探测

开放地址法哈希实现——二次探测法_chengqiuming的博客-CSDN博客_二次探测法

【干货】C++哈希桶（开链法解决哈希冲突）类的实现_weixin_34206899的博客-CSDN博客