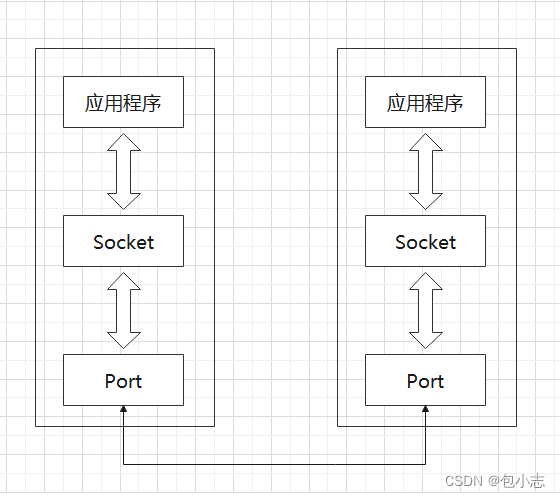
1.图像直方图概念
图像有很多基础概念,在我们学习的过程中因为一些原因无法涉及,但这并不代表它们不重要
今天,我们就来介绍一个概念——图像直方图
图像直方图,是图像处理中很重要的一个基础概念,
有很多的算法,比如传统的特征工程,跟它都有千丝万缕的关系
图像直方图是图像像素值的统计学特征。
由于其计算代价较小,且具有图像平移、旋转、缩放不变性等众多优点,广泛地应用于图像处理的各个领域,特别是灰度图像的阈值分割、基于颜色的图像检索以及图像分类、反响投影跟踪。
图像直方图常见的分为:
灰度直方图
颜色直方图
示例如下

图像直方图(Image Histogram)是用以表示数字图像中亮度分布的直方图,标绘了图像中每个亮度值的像素数。这种直方图中
横坐标的左侧为纯黑、较暗的区域,
右侧为较亮、纯白的区域。
因此一张较暗图片的直方图中的数据多集中于左侧和中间部分,而整体明亮、只有少量阴影的图像则相反。
CV 领域常借助图像直方图来实现图像的二值化。图像直方图中,也有直方图的两个概念
bin——bin是的X轴上每一组的长度,比如组长为1,就是bin中包含1个像素值。
bin由bins和取值范围决定
bins——binsX轴上的组数,对于像素值取值在0~255之间,如果bins = 256,则bin = 1
此外对于该取值范围来说,bins还可以有16、32、48、128等。
但一定要满足,256除以bin的大小应该是整数
简单来说,图像直方图就是对图像像素数据进行统计的一种方法
一幅灰度图像:图像直方图将0-255不同值分布在坐标系的X轴上,对应像素值的数量分布在Y轴上。
当bins=256时,此时(100,50),就表示值是100的像素有50个。
说明:
图像直方图可以唯一标识一张图像吗?
通常直方图的维数要低于原始数据,所以它的信息有缺,图像直方图并不能唯一表示一张图像。
那什么可以作为图像的"DNA",唯一标识一张图像呢?
特征工程就可以,这种真正的特征描述值会把图像变成一堆向量。
有很多种的法可以做特征工程,比如传统图像处理的特征提取
2.绘制彩色图像的一维直方图
API应用
calcHist
calcHist
计算一维数组的直方图(输入图像可以有多通道)
共10个参数
第1个参数 图像数组
第2个参数 输入图像数量
第3个参数 通道数组
第4个参数 可选mask
第5个参数 输出直方图数据(值与对应频次)的n维数组
第6个参数 直方图维数
当通道为1个时,我们选择维度为1维,此时直方图数据就为一维数组
当维度为2个时,我们选择维度为2维,此时直方图数据就为二维数组
………………
也就是说,n张图像 每张图像m个通道 也可以计算出相应的直方图数据
但对于绘制来说,一般都只绘制到2维,3维及以上就很复杂了
第7个参数 histSize( bins数组,x轴长度)
第8个参数 ranges(取值范围数组)
//以下参数暂时用不到
第9个参数 指示直方图bin间隔是否一致
默认为true,即等间隔取值
如果为false,则range不能写{0,255}这种,就要写{1,1,……,1}这种
第10个参数 累计标志(默认为false)
当多张图像的时候,
如果为true,则绘制直每张方图的时候,不会从头清空
会在前者直方图的基础上继续
cvRound
cvRound
将浮点数四舍五入到最近的整数
共1个参数
第1个参数 要处理的浮点数本课中计算的直方图维数为1维,采取方式为:
先把bgr三通道分离
然后进行每个通道的直方图数据计算,得到一维数组
再然后对直方图一维数组进行归一化处理
最后利用直方图一维数组绘制直方图
为什么这里要归一化呢?
因为一张图中,有些值的频次会过大,不方便绘制直方图
为什么还要要利用得到的数据数组绘制,而不是直接显示它?
因为计算的到直方图数据数组,是一个大小为256的一维数组,它的每个值对应一个频次
当我们用cout输出直方图数据,会得到256 * 1的列矩阵
直接显示这个数组的话就是如下。
实例代码:
//函数定义
void showHistogram_demo(Mat& image);
//函数实现
void QuickDemo::showHistogram_demo(Mat& image) {
//三通道分离
std::vector<Mat> bgr;
split(image, bgr);
//定义参数变量
const int channels[1] = { 0 };
Mat b_hist, g_hist, r_hist;
const int bins[1] = { 256 };
float xrange[2] = { 0,255 };
const float* ranges[1] = { xrange };
//计算Blue,Green,Red三通道各自的直方图
calcHist(&bgr[0], 1, channels, Mat(), b_hist, 1, bins, ranges);
calcHist(&bgr[1], 1, channels, Mat(), g_hist, 1, bins, ranges);
calcHist(&bgr[2], 1, channels, Mat(), r_hist, 1, bins, ranges);
//imshow("00", b_hist);
//std::cout << b_hist;
//显示直方图
int hist_w = 512;
int hist_h = 400;
int bin_w = cvRound((double)hist_w / bins[0]);
Mat histImage = Mat::zeros(Size(hist_w, hist_h), CV_8UC3);
//归一化直方图数据为指定范围
normalize(b_hist, b_hist, 0, hist_h, NORM_MINMAX, -1, Mat());
normalize(g_hist, g_hist, 0, hist_h, NORM_MINMAX, -1, Mat());
normalize(r_hist, r_hist, 0, hist_h, NORM_MINMAX, -1, Mat());
//绘制直方图曲线
for (int i = 0; i < 256; i++) {
Point p01(bin_w * i, hist_h - cvRound(b_hist.at<float>(i)));
/*
第一个点横向坐标:bin_w*i: 即 512/256 再 * i
第二个点纵向坐标:直方图纵高 - 根据直方图纵高归一化后的频次,即为纵向坐标
当频次很低时,减的少,就靠下,反之靠上
*/
//线段的下一个点
Point p02(bin_w * i + 1, hist_h - cvRound(b_hist.at<float>(i + 1)));
Point p11(bin_w * i, hist_h - cvRound(g_hist.at<float>(i)));
Point p12(bin_w * i + 1, hist_h - cvRound(g_hist.at<float>(i + 1)));
Point p21(bin_w * i, hist_h - cvRound(r_hist.at<float>(i)));
Point p22(bin_w * i + 1, hist_h - cvRound(r_hist.at<float>(i + 1)));
line(histImage, p01, p02, Scalar(255, 0, 0), 1, 8, 0);
line(histImage, p11, p12, Scalar(0, 255, 0), 1, 8, 0);
line(histImage, p21, p22, Scalar(0, 0, 255), 1, 8, 0);
}
imshow("直方图", histImage);
}


初印象.assets/image-20221116223203420.png)