欧拉图

• 在连通图G中，经过G的每条边一次且仅一次的通路，称为欧拉通路
• 若欧拉通路为回路，则称为欧拉回路
• 含有欧拉回路的图称为欧拉图
• 有欧拉通路则G可以一笔画出
• 有欧拉回路则G是连通的且无奇点（欧拉图无奇点）

哈密顿图

• 在连通图G中，经过G的每个顶点一次且仅一次的通路，称为哈密顿路，若哈密顿路为回路，则称为哈密顿回路。 含有哈密顿回路的图称为哈密顿图。
• 哈密顿图关注的是顶点

试题 

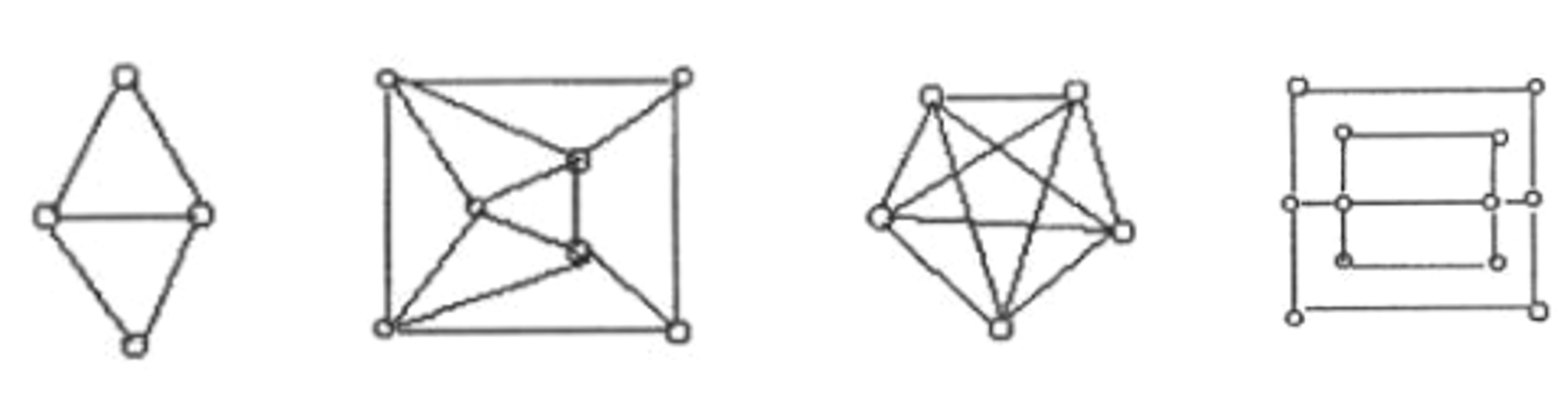
下列图中，是欧拉图的为（ ） 。

【答案】C，每个顶点都为偶数是欧拉图

下列关于欧拉图的描述正确的是（ ）。

A、完全图都是欧拉图

B、K4是欧拉图

C、K5是欧拉图

D、K6是欧拉图 

【答案】C，K5是顶点个数为5的完全图，每个顶点的度数都为4，都为偶数因此是欧拉图。

今有a，b，c，d，e，f，g 7人，已知下列事实：a会讲德语；b会讲法语和德语；c会讲俄语和英语；d会讲日语和汉语；e会讲德语和汉语；f会讲法语、日语和俄语；g会讲英语和汉语。 试问：这7人应如何排座位（按圆桌排），才能使每个人和他身边的人交谈？

【答案】

若两人有共同语言，在两人之间画一条边，则可得到如下连通图G 将这7人圆桌排座位，使得每个人都能和他身边的人交谈，就是在图G中找哈密顿回路 经观察，图G中有两条哈密顿回路： abfcgdea aedgcfba

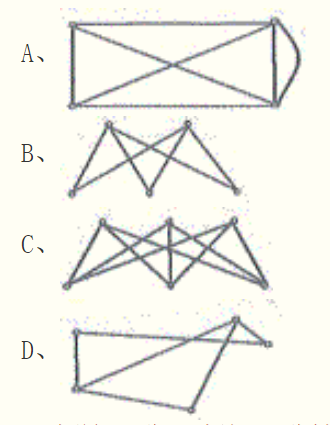
下列图中不是哈密顿图的是（）。 

【答案】B，给定无向图G，若存在一条路L，经过图中每个顶点一次且仅一次，则L称为哈密顿路；若存在一条回路C，经过图中的每个顶点一次且仅一次，C称作哈密顿回路。具有哈密顿回路的图称作哈密顿图。B选项不是哈密顿图。