树与二叉树（考研版）

news2024/11/6 7:19:07

文章目录

  • 树与二叉树
    • 树的基本概念
      • 结点、树属性的描述
      • 树的性质
    • 二叉树的概念
      • 二叉树的性质
      • 二叉树的构建
      • 二叉树的遍历
        • 先序遍历
        • 中序遍历
        • 后序遍历
        • 层次遍历
      • 递归算法和非递归算法的转换
        • 源代码
    • 线索二叉树
      • 二叉树的线索化
      • 线索二叉树 找前驱/后继
    • 树和森林
      • 树的存储
    • 树与二叉树的应用
      • 哈夫曼树和哈夫曼编码
      • 并查集
    • 习题总结

树与二叉树

树的基本概念

树的定义是递归的，即在树的定义中又用到了其自身，树是一种递归的数据结构。同时是一种分层结构，具有以下两个特点：

  • 树的根节点没有前驱，除根节点外所有结点有且只有一个前驱。
  • 树中所有结点都可以有零个或多个后继。

特点：树适合于表示具有层次结构的数据。

结点、树属性的描述

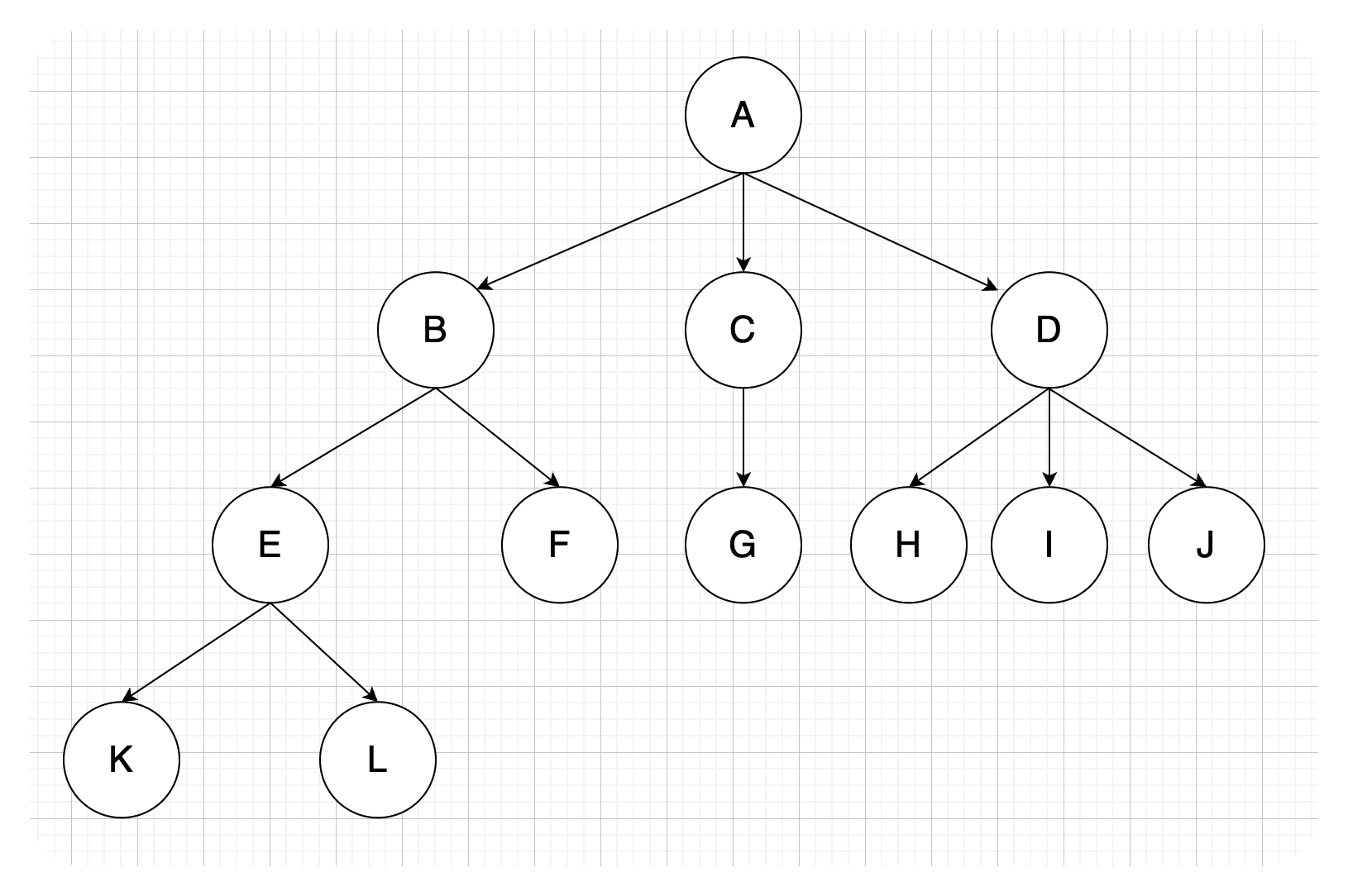
image-20230814105154507

  1. 树中一个结点的孩子个数称为该结点的度，树中结点的最大度数称为树的度。

    • 结点的度：有几个孩子（分支）
    • 树的度：各结点的度的最大值

    如结点B的度为 2，结点D的度为 3，树的度为 3，剩余结点的度数都小于3，因此这颗树的度为3。

  2. 结点的深度、高度和层次

    结点的深度：从上往下数（默认从 1 开始）

    结点的高度：从下往上数

    树的层次：总共多少层

树的性质

树具有如下最基本的性质：

  1. 结点数 = 总度数 + 1

    结点的度：结点有几个孩子（分支）

    eg:【2010统考真题】在一棵度为4的树 T T T中，若有20个度为4的结点，10个度为3的结点，1个度为2的结点，10个度为1的结点，则树 T T T的叶子结点个数是（ B B B ）

    A . 41 A.41 A.41 B . 82 B.82 B.82 C . 113 C.113 C.113 D . 122 D.122 D.122

    结点数：20 + 10 + 1 + 10 + X 叶子 X_{叶子} X叶子​ = 41 + X 叶子 X_{叶子} X叶子​

    总度数：20*4 + 10*3 + 1*2 + 10*1 = 122

    结点数 = 总度数 + 1 => 41 + X 叶子 X_{叶子} X叶子​ = 122 + 1 => X 叶子 X_{叶子} X叶子​ = 122 + 1 - 41 = 82

  2. 度为m的树和m叉树的区别

    • 树的度：各结点的度的最大值
    • m叉树：每个结点最多只能有m个孩子的树
    度为m的树m叉树
    任意结点的度≤m（最多m个孩子）任意结点的度≤m（最多m个孩子）
    至少有一个结点度=m（有m个孩子）允许所有结点的度都＜m
    一定是非空树，至少有m+1个结点可以是空树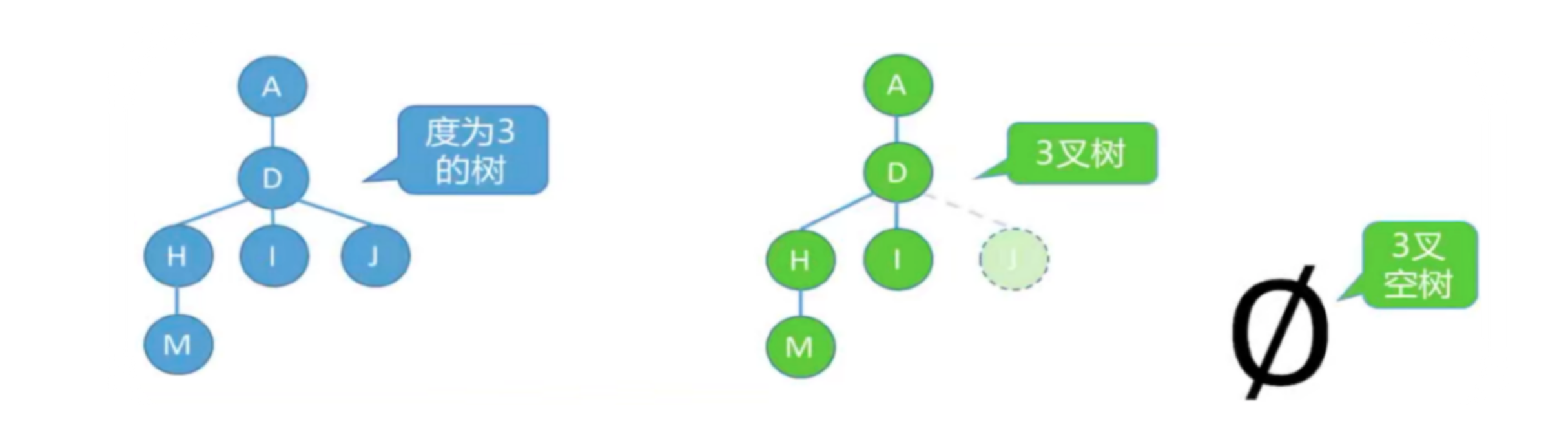

    image-20231018103748096

  3. 度为 m m m的树第 i i i层至多有 m i − 1 m^{i -1} mi−1个结点， m m m叉树第 i i i层至多有 m i − 1 m^{i - 1} mi−1个结点

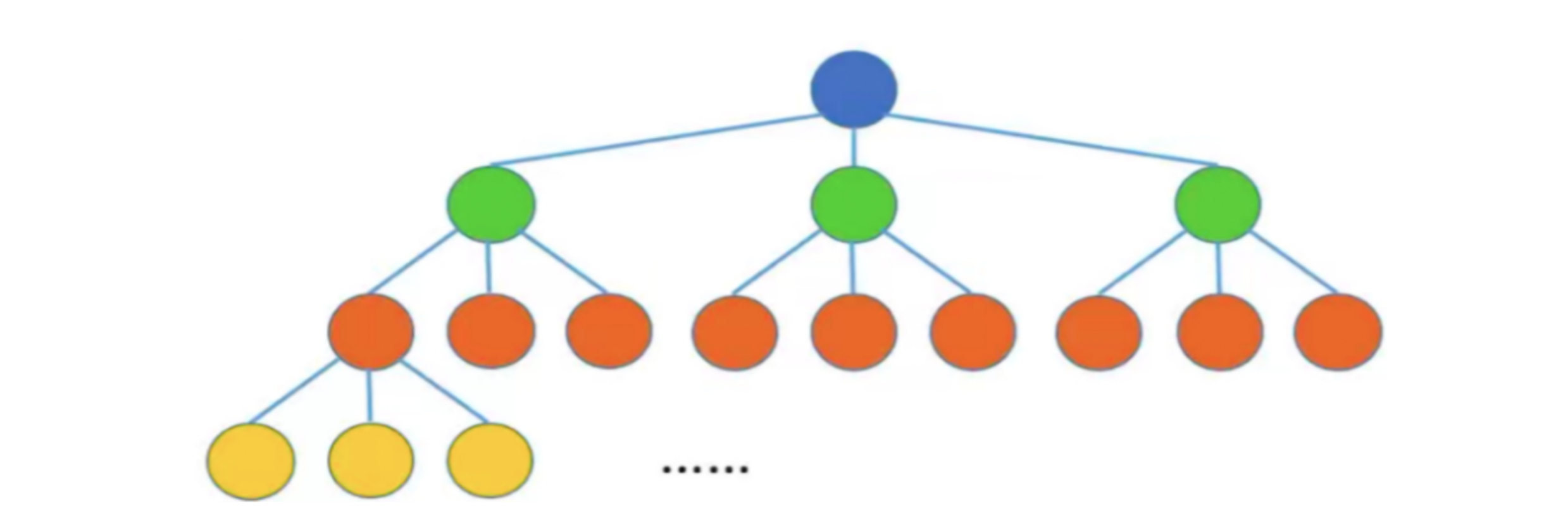
    image-20231018104043065

  4. 高度为 h h h的 m m m叉树至多有 m h − 1 m − 1 \frac {m^{h} - 1}{m -1} m−1mh−1​个结点

    等比数列求和公式：
    a + a q + a q 2 + ⋅ ⋅ ⋅ + a q n − 1 = a ( 1 − q n ) 1 − q a + aq + aq^2 + ··· + aq^{n - 1} = \frac{a(1-q^n)}{1-q} a+aq+aq2+⋅⋅⋅+aqn−1=1−qa(1−qn)​

    每层的结点求和即 m 0 + m 1 + m 2 + ⋅ ⋅ ⋅ ⋅ + m h − 1 m^0 + m^1 + m^2 + ····+ m^{h-1} m0+m1+m2+⋅⋅⋅⋅+mh−1，利用等比数列求和即可。

  5. 高度为 h h h的 m m m叉树至少有 h h h个结点，高度为 h h h、度为 m m m的树至少有 h + m − 1 h+m-1 h+m−1个结点。

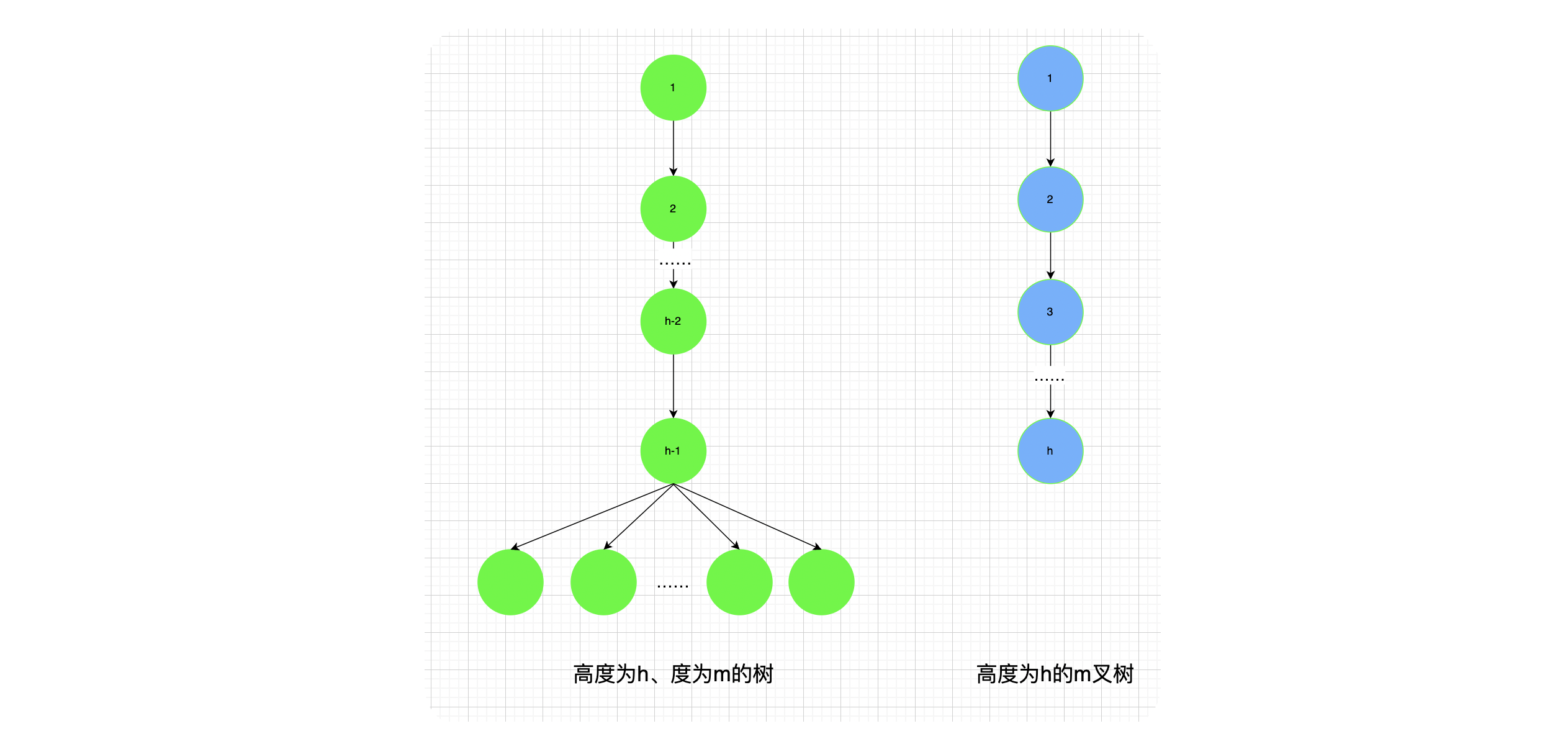
    image-20231023195851022

  6. 具有n个结点的m叉树的最小高度为 ⌈ l o g m ( n ( m − 1 ) + 1 ) ⌉ \lceil log_m(n(m -1) + 1) \rceil ⌈logm​(n(m−1)+1)⌉

    高度最小的情况：所有结点都有 m m m个孩子

    证明过程如下：前 h − 1 h-1 h−1层最多有$\frac {m^{h -1} - 1}{m - 1} 个结点，前 h 层最多有 个结点，前h层最多有 个结点，前h层最多有\frac {m^{h} - 1}{m - 1} $个结点
    m h − 1 − 1 m − 1 < n ≤ m h − 1 m − 1 m h − 1 < n ( m − 1 ) + 1 ≤ m h h − 1 < l o g m ( n ( m − 1 ) + 1 ) ≤ h h m i n = ⌈ l o g m ( n ( m − 1 ) + 1 ) ⌉ \frac {m^{h -1} - 1}{m - 1} < n ≤ \frac {m^{h} - 1}{m - 1}\\ m^{h-1} < n(m -1) + 1 ≤ mh\\ h - 1 < log_m(n(m - 1) + 1) ≤ h\\ h_{min} =\lceil log_m(n(m -1) + 1) \rceil m−1mh−1−1​<n≤m−1mh−1​mh−1<n(m−1)+1≤mhh−1<logm​(n(m−1)+1)≤hhmin​=⌈logm​(n(m−1)+1)⌉

二叉树的概念

本章需要着重讨论的是二叉树（Binary Tree）。

二叉树是一种特殊的树形结构，其特点是每个节点至多只有两棵子树（即二叉树中不存在度大于2的结点），并且二叉树的子树有左右之分，其次序不能任意颠倒。一棵二叉树大概长这样：

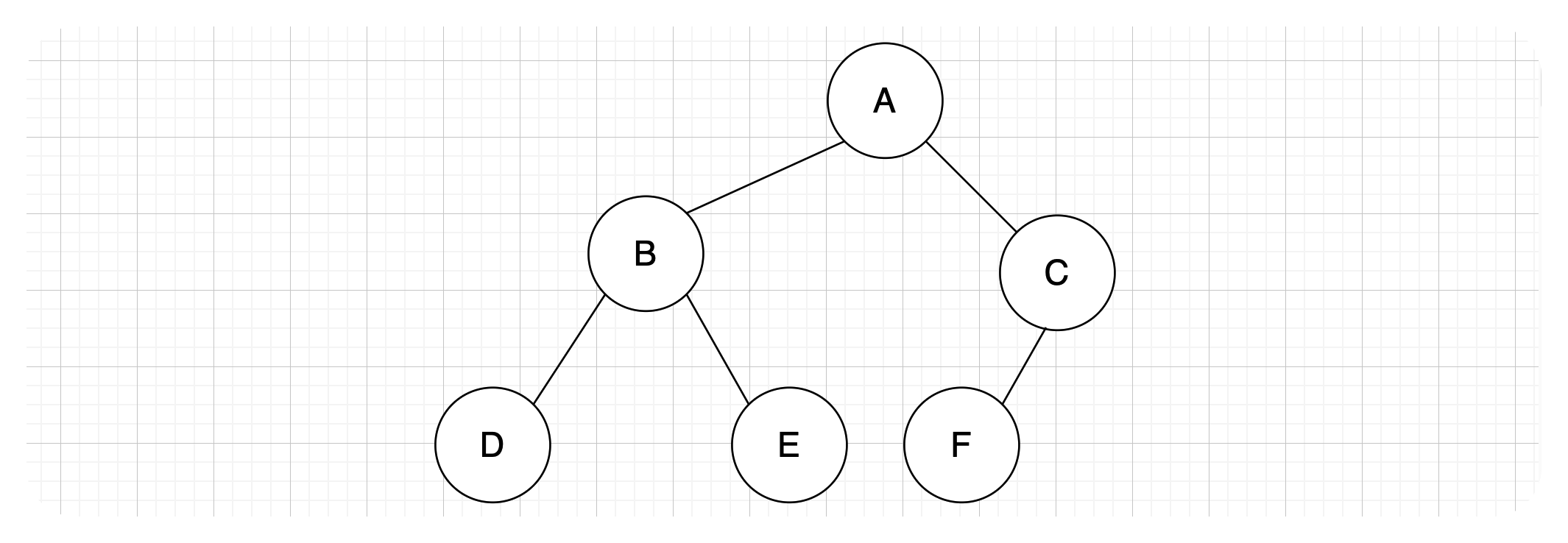
image-20230816215503084

并且二叉树任何结点的子树是有左右之分的，不能颠倒顺序，比如A结点左边的子树，称为左子树，右边的子树称为右子树。

二叉树有 5 中基本形态，分别是：

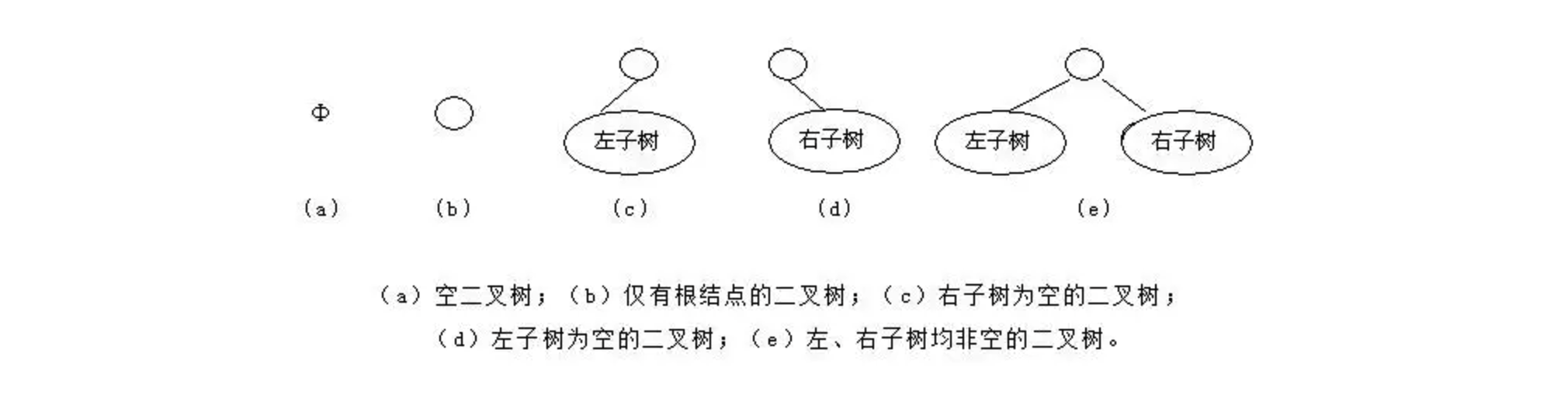
image-20230816215719603

几种特殊的二叉树

  1. 满二叉树：在一棵二叉树中，所有分支结点都存在左子树和右子树，且叶子结点都在同一层。

  2. 完全二叉树：只有最后一层有空缺，并且所有的叶子结点是按照从左往右的顺序排列的。所以，一棵满二叉树，一定是一棵完全二叉树。

  3. 二叉排序树：可用于元素的排序、搜索

    左子树上所有结点的关键字均小于根结点的关键字

    右子树上所有结点的关键字均大于根结点的关键字

    左子树和右子树又各是一颗二叉排序树

  4. 平衡二叉树：能更高的搜索效率

    树上任意一个结点的左子树和右子树的深度之差不超过 1。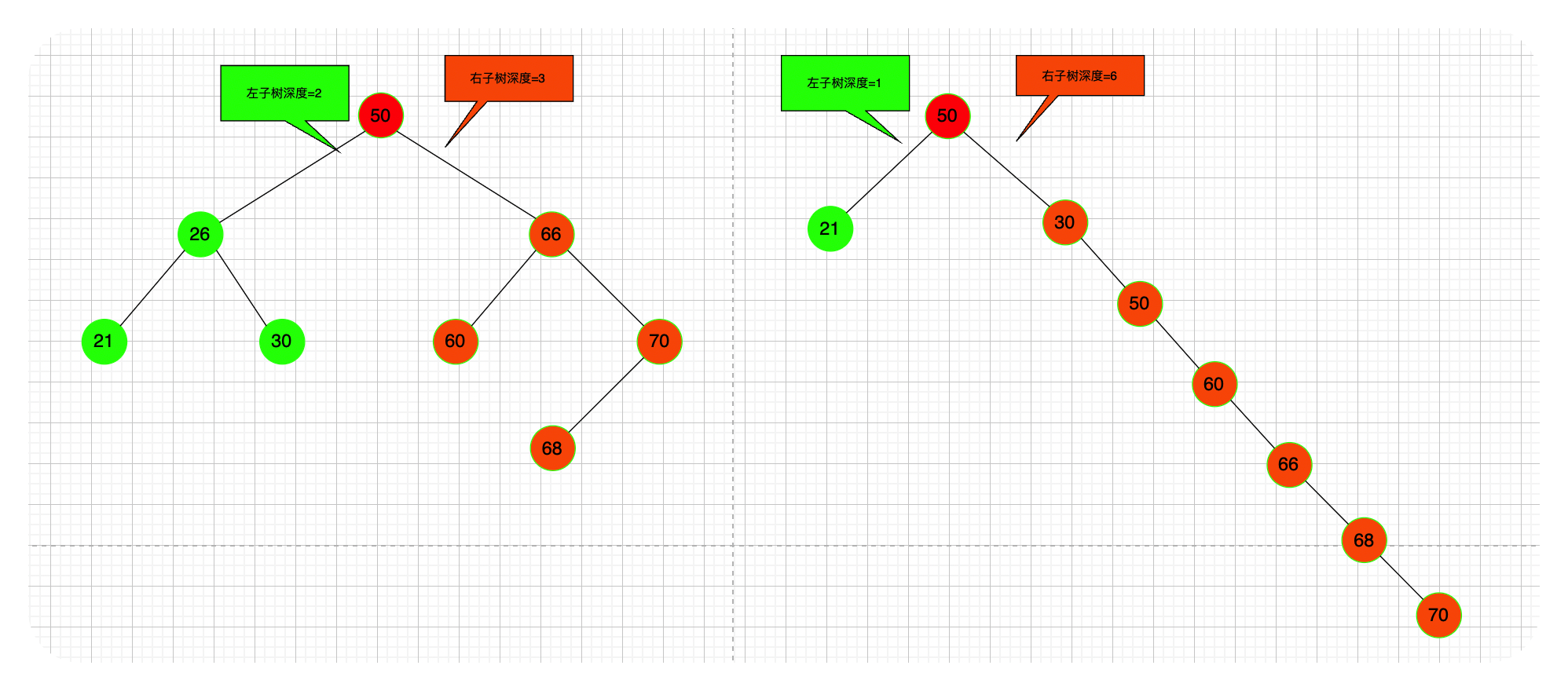

    image-20230817223558916

二叉树的性质

假设一棵二叉树中结点总数为 n n n，度为0、1、2的结点数量分别为 n 0 n_0 n0​、 n 1 n_1 n1​、 n 2 n_2 n2​，结点的边数为 E E E.

性质一：非空二叉树上的叶子节点数等于度为2的结点树加1，即 n 0 = n 2 + 1 n_0 = n_2 + 1 n0​=n2​+1。

由于一棵二叉树中只有这三种类型的结点，那么可以直接得到结点总数：
n = n 0 + n 1 + n 2 n = n_0 + n_1 + n_2 n=n0​+n1​+n2​
接下来换一个思路，从边的数量上考虑。因为每个结点有且仅有一条边与其父结点相连，那么边数之和就可以表示为：
E = n 1 + 2 n 2 E = n_1 + 2n_2 E=n1​+2n2​

度为 1 的结点有一条边，度为 2 的结点有两条边，度为 0 的结点没有边。

根据前面树的基本性质可知，结点的边数为 E = n − 1 E = n - 1 E=n−1。因此，可以得到另一个计算结点总数的方式（结合公式 (3)(4)）得：
E = n − 1 = n 1 + 2 n 2 ( 公式 4 ) n = n 1 + 2 n 2 + 1 n = n 1 + 2 n 2 + 1 = n 0 + n 1 + n 2 ( 公式 3 ) n 0 = n 2 + 1 E = n - 1 = n_1 + 2n_2(公式 4)\\ n = n_1 + 2n_2 + 1\\ n = n_1 + 2n_2 + 1 = n_0 + n_1 + n_2(公式 3)\\ n_0 = n_2 +1 E=n−1=n1​+2n2​(公式4)n=n1​+2n2​+1n=n1​+2n2​+1=n0​+n1​+n2​(公式3)n0​=n2​+1

性质二：非空二叉树上第k层上至多有 2 k − 1 ( k ≥ 1 ) 2^{k - 1}(k≥1) 2k−1(k≥1)个结点。

第一层至多有 2 1 − 1 2^{1-1} 21−1个结点，第二层至多有 2 2 − 1 = 2 2^{2-1} = 2 22−1=2个结点，以此类推，可以证明其为一个公比为 2 的等比数列 2 k − 1 2^{k-1} 2k−1。

性质三：高度为k的二叉树至多有 2 k − 1 2^k - 1 2k−1个结点 ( h ≥ 1 ) (h≥1) (h≥1)

对于一棵深度为k的二叉树，可以具有的最大结点数量为：
n = 2 0 + 2 1 + 2 2 + . . . + 2 k − 1 n = 2^0 + 2^1 + 2^2 + ...+ 2^{k - 1} n=20+21+22+...+2k−1
实际上每一层结点数量构成了一个以公比q = 2的等比数列，结合等比数列求和公式得：
S n = a 1 × ( 1 − q n ) 1 − q = 1 × ( 1 − 2 k ) 1 − 2 = − ( 1 − 2 k ) = 2 k − 1 S_n = \frac {a_1 × (1 - q_n)}{1 - q} = \frac{1×(1 - 2^k)}{1 - 2} = -(1 - 2^k) = 2^k - 1 Sn​=1−qa1​×(1−qn​)​=1−21×(1−2k)​=−(1−2k)=2k−1

性质四：

对一棵有n个结点、深度为k的完全二叉树按从上到下、从左到右的顺序依次编号 1,2，···，n，现在对于任意一个结点i有以下关系：

  1. 对于一个拥有左右孩子的结点i来说，其左孩子为2i，右孩子为2i+1。
  2. 如果i = 1，那么此结点为二叉树的根节点；如果i > 1，那么其父结点就是 ⌊ i / 2 ⌋ \lfloor i/2 \rfloor ⌊i/2⌋，比如第三个结点的父节点为第1个结点，也就是根节点。
  3. 如果2i > n，则结点i没有左孩子，比如下图中的二叉树，n为5，假设此时i = 3，那么2i = 6 > n = 5，说明第三个结点没有左孩子。
  4. 如果2i + 1 > n，则结点i没有右孩子。

image-20230817102327675

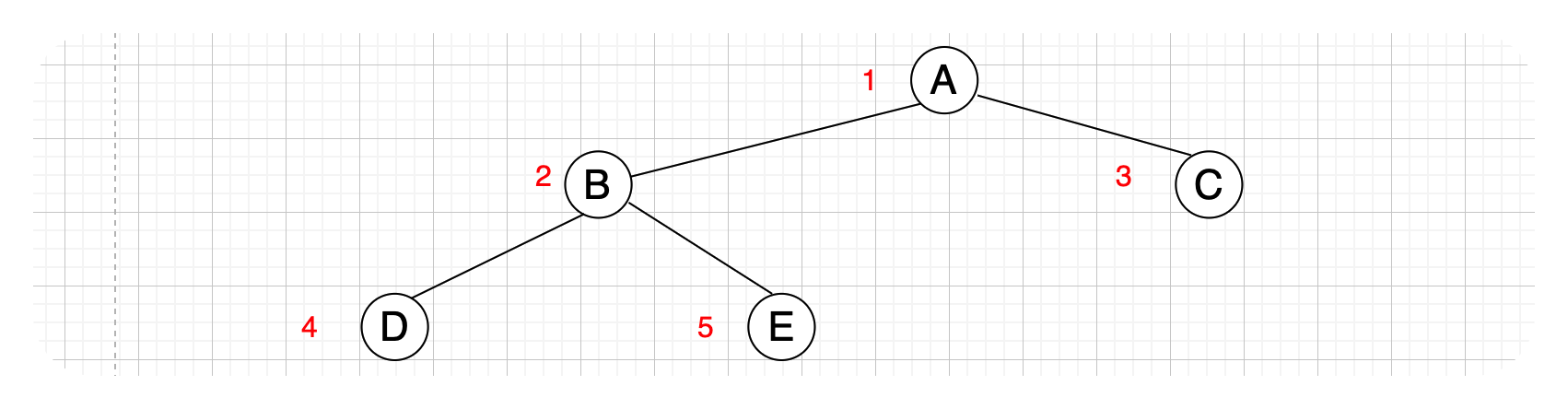
性质五：一棵具有n个结点的**完全二叉树**深度为 k = ⌊ l o g 2 n + 1 ⌋ k = \lfloor log_2n + 1 \rfloor k=⌊log2​n+1⌋。

完全二叉树除了最后一层有空缺外，其他层数都是饱满的。假设这棵二叉树为满二叉树，那么根据我们前面得到的性质，假设层数为k层，那么总结点数量为 n = 2 k − 1 n = 2^k - 1 n=2k−1；根据完全二叉树性质，最后一层可满可不满(1～k-1层为满二叉树的情况下，总结点数 2 k − 1 − 1 2^{k - 1} - 1 2k−1−1)，那么一棵完全二叉树结点的总结点数n满足：
2 k − 1 − 1 < n ≤ 2 k − 1 2^{k - 1} - 1 < n ≤ 2^k - 1 2k−1−1<n≤2k−1
因为n是一个整数，那么可以写成：
2 k − 1 ≤ n ≤ 2 k − 1 2^{k - 1} ≤ n ≤ 2^k - 1 2k−1≤n≤2k−1
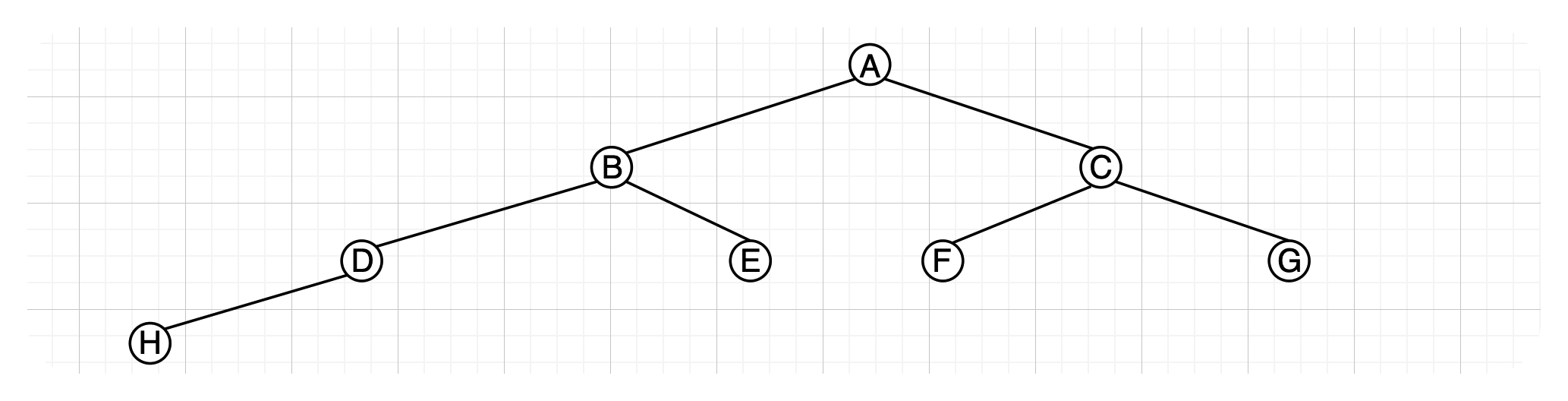
image-20230817105143997

这里左边可以取等号的情况如上图所示，该树为完全二叉树的极端情况。

现在只看左边的不等式，两边取对数得：
k − 1 ≤ l o g 2 n k - 1 ≤ log_2n k−1≤log2​n
综上所述，一棵具有n个结点的完全二叉树深度为 k = ⌊ l o g 2 n + 1 ⌋ k = \lfloor log_2n + 1\rfloor k=⌊log2​n+1⌋。

⚠️：性质五推导比较复杂，推荐直接记忆✌️。

二叉树练习题

  1. 由三个结点可以构造出多少种不同的二叉树？

    手画直接的到结果，一共是五种。但是，如果要求N个结点的话如何求解呢？可以利用动态规划，接下来我们分析一下：

    • 假设现在没有结点或者一个结点，那么只有一种情况 h ( 0 ) = h ( 1 ) = 1 h(0) = h(1) = 1 h(0)=h(1)=1

    • 假设现在有两个结点，其中一个为根节点，剩下的一个结点可以为左结点或右结点。如果为左结点，那么右边 0 个结点；如果为右结点，那么左边 0 个结点，则 h ( 2 ) = h ( 1 ) × h ( 0 ) + h ( 0 ) × h ( 1 ) = 2 h(2) = h(1)×h(0) + h(0)×h(1) = 2 h(2)=h(1)×h(0)+h(0)×h(1)=2

    • 假设现在有三个结点，其中一个为根节点，剩下的两个结点情况就有三种情况，两个都在左边或者右边，或者一边一个，则 h ( 3 ) = h ( 2 ) × h ( 0 ) + h ( 1 ) × h ( 1 ) + h ( 0 ) × h ( 0 ) = 2 + 1 + 2 = 5 h(3) = h(2) × h(0) + h(1) × h(1) + h(0) × h(0) = 2 + 1 + 2 = 5 h(3)=h(2)×h(0)+h(1)×h(1)+h(0)×h(0)=2+1+2=5

    • 总结：N每次加一，项数就会多一项，所以只需要按照规律把所有情况的结果相加即可。

    #include <stdio.h>

int main() {
    int n;
    scanf("%d", &n);
    int dp[n + 1];
    dp[0] = dp[1] = 1;
    for (int i = 2; i <= n; ++i) {
        dp[i] = 0;
        for (int j = 0; j < i; ++j) {
            dp[i] += dp[i - j - 1] * dp[j];
        }
    }
    printf("%d",dp[n]);
}

    image-20230817221736114

【2009年统考真题】已知一棵完全二叉树的第6层（设根为第1层）有8个叶结点，则该完全二叉树的结点个数最多是（C）

A . 39 A.39 A.39 B . 53 B.53 B.53 C . 111 C.111 C.111 D . 119 D.119 D.119

解：第6层最多 2 6 − 1 = 32 2^{6-1} = 32 26−1=32个结点，8个叶结点，则剩下的24个结点均有左右孩子（满足最多结点个数），即第7层有24*2=48个结点，前6层一共有 2 6 − 1 = 63 2^{6} - 1 = 63 26−1=63个结点，所有最多有 63 + 48 = 111 63 + 48 = 111 63+48=111个结点。

二叉树的构建

定义结构体

typedef char E;

typedef struct TreeNode {
    E element;
    struct TreeNode *left, *right;
} TreeNode, *Node;

假设我们要构建这个二叉树，首先我们要创建好这几个结点：

int main() {
    Node a = malloc(sizeof(TreeNode));
    Node b = malloc(sizeof(TreeNode));
    Node c = malloc(sizeof(TreeNode));
    Node d = malloc(sizeof(TreeNode));
    Node e = malloc(sizeof(TreeNode));
    a->element = 'A';
    b->element = 'B';
    c->element = 'C';
    d->element = 'D';
    e->element = 'E';
}

然后从上往下，依次连接每一个结点，并且测试是否连接成功：

int main() {
  	//创建结点代码....
    a->left = b;
    a->right = c;
    b->left = d;
    b->right = e;
    c->left = c->right = NULL;
    d->left = d->right = NULL;
    e->left = e->right = NULL;

    printf("%c", a->left->left->element);
}

注意：这里需要将叶子结点或者其他只有一个结点的另一个空结点设置为NULL。

image-20230818161314400

与此同时，我们在printf函数部分设置断点debug：

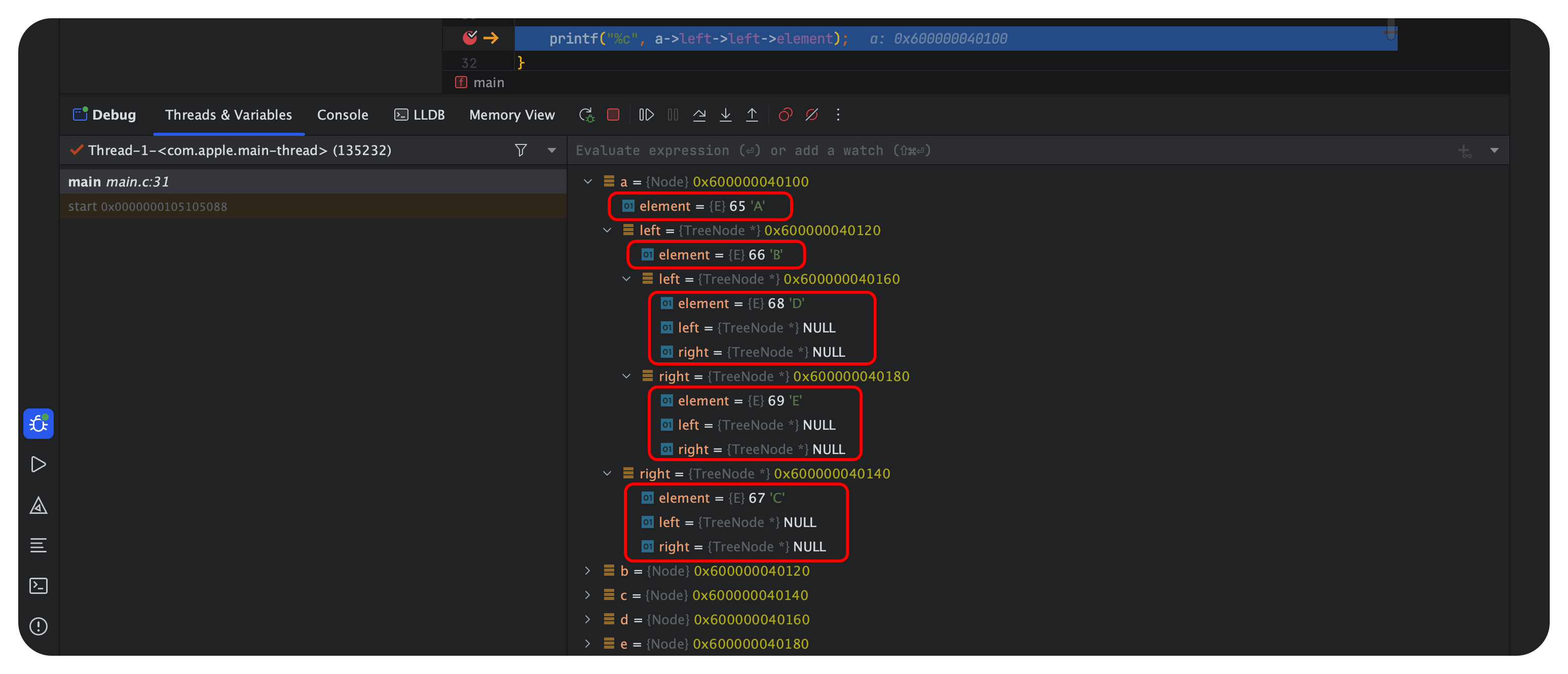
image-20230818161512585

二叉树的遍历

前面通过使用链式结构，成功构建出了一棵二叉树，接着我们来看看如何遍历一棵二叉树，也就是说想要访问二叉树的每一个结点。由于树形结构特殊，遍历顺序并不唯一，所以一共有四种访问方式：**先序遍历、中序遍历、后序遍历、层序遍历。**不同的访问方式输出都结点顺序也不同。

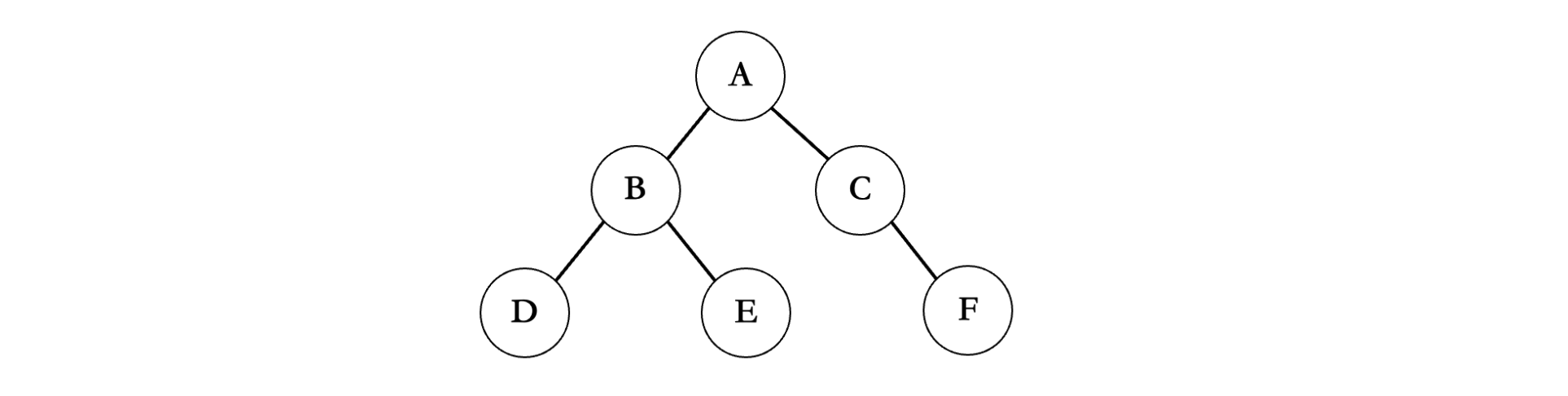
image-20230818163536147

首先需要将这棵二叉树组装好，这一步比较繁琐，无可避免🥺🥺🥺

int main() {
    Node a = malloc(sizeof(TreeNode));
    Node b = malloc(sizeof(TreeNode));
    Node c = malloc(sizeof(TreeNode));
    Node d = malloc(sizeof(TreeNode));
    Node e = malloc(sizeof(TreeNode));
    Node f = malloc(sizeof(TreeNode));
    a->element = 'A';
    b->element = 'B';
    c->element = 'C';
    d->element = 'D';
    e->element = 'E';
    f->element = 'F';

    a->left = b;
    a->right = c;
    b->left = d;
    b->right = e;
    c->right = f;
    c->left = NULL;
    d->left = d->right = NULL;
    e->left = e->right = NULL;
    f->left = f->right = NULL;
}
先序遍历

先序遍历是一种勇往直前的态度，走到哪就遍历到那里，先走左边再走右边，比如上面的这个图，首先会从根节点开始：从A开始，先左后右，那么下一个就是 B，然后继续走左边，左边为 D；现在 ABD 走完之后，B 的左边结束了，那么就要从 B 的右边开始了，因此下一个是 E；E 结束之后，现在 A 的左子树已经完全遍历完成了。然后就是 A 的右边，接着就是 C，C 没有左子树，直接走右边，最后输出 F；所以上面这个二叉树的前序遍历结果为：ABDECF。

先序遍历（preOrder）的操作过程如下：若二叉树为空，则什么也不做；否则

  1. 打印根节点
  2. 先序遍历左子树
  3. 先序遍历右子树

接下来就是编写实现先序遍历的函数了。我们传入的是根节点，根据先序遍历的特点，不难发现先序遍历中，根节点一直都是先沿着左子树“勇往直前”，直到走到了尽头，再走右子树，如此循环往复，递归函数就具有这个特点。当走到一个结点的时候，我们就打印对应的元素。那么如何结束这个递归函数呢？之前说过，递归函数有递归入口和终止条件，入口已经有了，那么终止条件是什么呢？二叉树走到尽头，即结点的左右孩子都为NULL，那就表示已经到头了，直接返回即可。

因此有了下面的函数：

void perOrder(Node root) {   //传入二叉树根节点
    if (root == NULL) return;	//终止条件
    printf("%c", root->element);
    perOrder(root->left);
    perOrder(root->right);
}

最后在main函数中调用即可

int main() {
  	//组装二叉树函数
  	//...
    perOrder(a);
}

image-20230818164902786

那么先序遍历我们了解完了，接着就是中序遍历了，中序遍历在顺序上与先序遍历不同，先序遍历是走到哪就打印到哪，而中序遍历需要先完成整个左子树的遍历后再打印，然后再遍历其右子树。

中序遍历

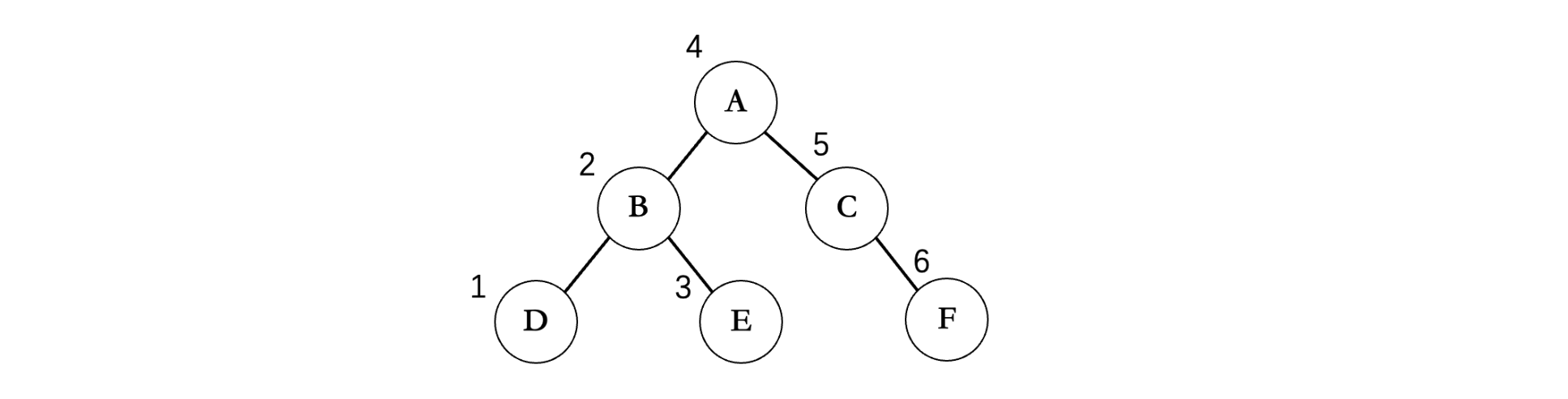
image-20230818170120172

还是以上面的二叉树为例，首先需要先不断遍历左子树，走到最底部，但是沿途并不进行打印，而是到底之后，再打印，所以第一个打印的是D，接着由于没有右子树，所以我们回到B，此时再打印B，然后再去看B的右结点E，由于没有左子树和右子树了，所以直接打印E；左边遍历完成，接着回到A，打印A，然后对A的右子树重复上述操作。所以说遍历的基本规则还是一样的，只是打印值的时机发生了改变。

中序遍历（inOrder）的操作过程如下：若二叉树为空，则什么也不做；否则，

  1. 中序遍历左子树
  2. 打印结点
  3. 中序遍历右子树

所以这棵二叉树的中序遍历结果为：DBEACF，我们可以发现一个规律，就是在某个结点的左子树中所有结点，其中序遍历结果也是按照这样的规律排列的，比如A的左子树中所有结点，中序遍历结果中全部都在A的左边，右子树中所有的结点，全部都在A的右边（这个规律很关键，后面在做一些算法题时会用到）。对应的递归算法如下：

void inOrder(Node root) {
    if (root == NULL) return;
    inOrder(root->left);
    printf("%c", root->element);
    inOrder(root->right);
}

image-20230818171833808

后序遍历

接着我们来看一下后序遍历，后序遍历继续将打印的时机延后，需要等待左右子树全部遍历完成，才会去进行打印。

首先还是一路向左，到达结点D，此时结点D没有左子树了，接着看结点D还有没有右子树，发现也没有，左右子树全部遍历完成，那么此时再打印D，同样的，D完事之后就回到B了，此时接着看B的右子树，发现有结点E，重复上述操作，E结点没有左子树，也没有右子树，E也打印出来了；接着B的左右子树全部OK，那么再打印B，接着A的左子树就完事了，现在回到A，看到A的右子树，继续重复上述步骤，当A的右子树也遍历结束后，最后再打印A结点。

后序遍历（postOrder）的操作过程如下：若二叉树为空，则什么也不做；否则，

  1. 后序遍历左子树
  2. 后序遍历右子树
  3. 打印结点

所以最后的遍历顺序为：DEBFCA，不难发现，整棵二叉树（包括子树）根结点一定是在后面的，比如A在所有的结点的后面，B在其子节点D、E的后面，这一点恰恰和前序遍历相反（注意不是得到的结果相反，是规律相反）

void postOrder(Node root) {
    if (root == NULL) return;
    postOrder(root->left);
    postOrder(root->right);
    printf("%c", root->element);
}

三种遍历算法中，递归遍历左、右子树的顺序都是固定的，只是访问根节点的顺序不同。不管采用哪种遍历算法，每个结点都访问一次，且仅访问一次，故时间复杂度都是 O ( n ) O(n) O(n)。在递归遍历中，递归工作栈的栈深恰好为树的深度，所以在最坏的情况下，二叉树是有 n n n个结点且深度为 n n n的单支树，遍历算法的空间复杂度为 O ( n ) O(n) O(n)。

层次遍历
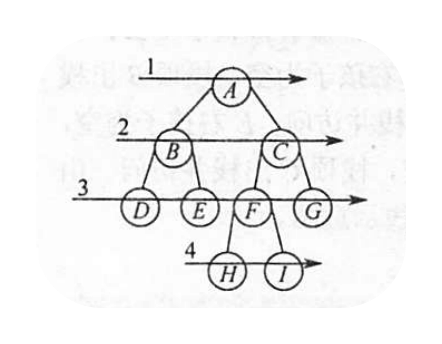图片描述   层次遍历如左图所示，即按照箭头所指方向，按照1,2,3,4 的层次顺序，对二叉树中的各个结点进行访问。
   要进行层次遍历，需要借助一个 队列。首先将二叉树根节点入队，然后出队，访问出队结点。若它右左子树，则将左子树根节点入队；若它有右子树，则将右子树根节点入队。完成入队后出队，访问出队结点……如此反复，直到队列为空。

二叉树的层次遍历算法如下：

void levelOrder(TNode root) {
    Queue queue;
    initQueue(&queue);
    EnQueue(&queue, root);  //根节点入队
    while (!isEmpty(&queue)) {      //不断重复，直到队列为空为止
        TNode node = DeQueue(&queue);//出队元素，并打印
        printf("%c", node->element);
        if (node->left)             //如果存在左还在，入队
            EnQueue(&queue, node->left);
        if (node->right)            //如果存在右孩子，入队
            EnQueue(&queue, node->right);
    }
}

image-20230820171456260

温故而知新，这里顺带复习了一下队列的相关内容，建议自己手写（或手敲）下列的所有内容，加以巩固练习。

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef char E;
typedef struct TreeNode {
    E element;
    struct TreeNode *left, *right;
} TreeNode, *TNode;

typedef TNode T;
typedef struct QueueNode {
    T element;
    struct QueueNode *next;
} QueueNode, *QNode;

typedef struct Queue {
    QNode front, rear;
} Queue, *LinkedQueue;

bool initQueue(LinkedQueue queue) {
    QNode node = malloc(sizeof(QueueNode));
    if (node == NULL) return 0;
    queue->front = queue->rear = node;
    return 1;
}

bool EnQueue(LinkedQueue queue, T element) {
    QNode node = malloc(sizeof(QueueNode));
    if (node == NULL) return 0;
    node->element = element;
    queue->rear->next = node;
    queue->rear = node;
    return 1;
}

bool isEmpty(LinkedQueue queue) {
    return queue->front == queue->rear;
}

T DeQueue(LinkedQueue queue) {
    T e = queue->front->next->element;
    QNode node = queue->front->next;
    queue->front->next = queue->front->next->next;
    if (queue->rear == node)
        queue->rear = queue->front;
    free(node);
    return e;
}

void levelOrder(TNode root) {
    Queue queue;
    initQueue(&queue);
    EnQueue(&queue, root);  //根节点入队
    while (!isEmpty(&queue)) {      //不断重复，直到队列为空为止
        TNode node = DeQueue(&queue);//出队元素，并打印
        printf("%c", node->element);
        if (node->left)             //如果存在左还在，入队
            EnQueue(&queue, node->left);
        if (node->right)            //如果存在右孩子，入队
            EnQueue(&queue, node->right);
    }
}

int main() {
    TNode a = malloc(sizeof(TreeNode));
    TNode b = malloc(sizeof(TreeNode));
    TNode c = malloc(sizeof(TreeNode));
    TNode d = malloc(sizeof(TreeNode));
    TNode e = malloc(sizeof(TreeNode));
    TNode f = malloc(sizeof(TreeNode));
    a->element = 'A';
    b->element = 'B';
    c->element = 'C';
    d->element = 'D';
    e->element = 'E';
    f->element = 'F';

    a->left = b;
    a->right = c;
    b->left = d;
    b->right = e;
    c->right = f;
    c->left = NULL;
    d->left = d->right = NULL;
    e->left = e->right = NULL;
    f->left = f->right = NULL;

    levelOrder(a);
}

递归算法和非递归算法的转换

非递归的写法，需要使用循环，但是就比较麻烦了。我们需要使用栈来帮助我们完成（实际上递归写法本质上也是在利用栈），我们依然是从第一个结点开始，先走左边，每向下走一步，先输出节点的值，然后将对应的结点丢到栈中，当走到尽头时，表示左子树已经遍历完成，接着就是从栈中依次取出栈顶节点，如果栈顶结点有右子树，那么再按照同样的方式遍历其右子树，重复执行上述操作，直到栈清空为止。

  • 一路向左，不断入栈，直到尽头
  • 到达尽头后，出栈，看看有没有右子树，如果没有就继续出栈，直到遇到有右子树的为止
  • 拿到右子树后，从右子树开始，重复上述步骤，直到栈清空

比如我们还是以上面的这棵树为例：

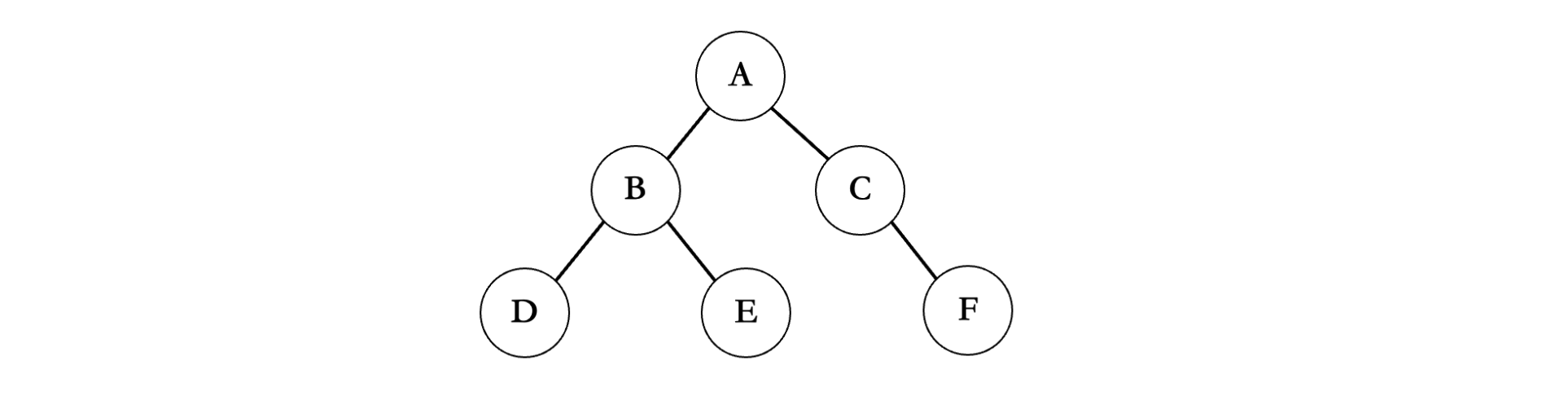
image-20230818163536147

首先我们需要自己创建栈和相对应的数据结构：

typedef char E;
typedef struct TreeNode {
    E element;
    struct TreeNode *left, *right;
} TreeNode, *TNode;

typedef TNode T;        //这里栈内元素类型定义为上面Node，也是二叉树结点指针
typedef struct StackNode {
    T element;
    struct StackNode *next;
} StackNode, *SNode;

//非递归操作
void initStack(SNode head) {
    head->next = NULL;
}

bool pushStack(SNode head, T element) {
    SNode node = malloc(sizeof(StackNode));
    if (node == NULL) return 0;
    node->element = element;
    node->next = head->next;
    head->next = node;
    return 1;
}

bool isEmpty(SNode head) {
    return head->next == NULL;
}

T popStack(SNode head) {
    SNode top = head->next;
    T e = head->next->element;
    head->next = head->next->next;
    free(top);
    return e;
}

创建完栈以后，接下来我们实现先序遍历的函数：

void perOrder(TNode root) {
    StackNode stack;
    initStack(&stack);
    while (root || !isEmpty(&stack)) {//栈为空且结点为 NULL 终止循环条件
        while (root) {//先不断遍历左子树，直到没有为止
            printf("%c", root->element);//打印当前结点元素值
            pushStack(&stack, root);//每经过一个结点，就将接待你放入栈中
            root = root->left;//继续遍历下一个左孩子结点
        }
        TNode node = popStack(&stack);//经过前面循环，左子树全部走完，接着走右子树
        root = node->right; //得到右孩子，重复上面的操作。
        // 如果没有右孩子，这里的 root 就被赋值为 NULL，下一轮循环直接跳过上面的 while，继续出站下一个结点找右子树
    }
}

注：在第一层 while 循环中调用isEmpty函数是因为防止到叶子结点的时候，其左右孩子都为空。当叶子结点的右孩子为空时，内层循环已经结束了，会调用外层的 while 循环，但是栈中可能还有其他元素，处于非空的状态。如果依然使用 root 判断，则会出错。

那么前序遍历我们了解完了，接着就是中序遍历了，中序遍历在顺序上与前序遍历不同，前序遍历是走到哪就打印到哪，而中序遍历需要先完成整个左子树的遍历后再打印，然后再遍历其右子树。

我们还是以上面的二叉树为例：首先需要先不断遍历左子树，走到最底部，但是沿途并不进行打印，而是到底之后，再打印，所以第一个打印的是D，接着由于没有右子树，所以我们回到B，此时再打印B，然后再去看B的右结点E，由于没有左子树和右子树了，所以直接打印E，左边遍历完成，接着回到A，打印A，然后对A的右子树重复上述操作。所以说遍历的基本规则还是一样的，只是打印值的时机发生了改变。

  1. 中序遍历左子树
  2. 打印结点
  3. 中序遍历右子树

所以这棵二叉树的中序遍历结果为：DBEACF，我们可以发现一个规律，就是在某个结点的左子树中所有结点，其中序遍历结果也是按照这样的规律排列的，比如A的左子树中所有结点，中序遍历结果中全部都在A的左边，右子树中所有的结点，全部都在A的右边（这个规律很关键，后面在做一些算法题时会用到）

void inOrder(TNode root){
    StackNode stack;
    initStack(&stack);
    while (root || !isEmpty(&stack)) {       //栈为空且结点为 NULL 终止循环条件
        while (root) {//先不断遍历左子树，直到没有为止
            pushStack(&stack, root);//每经过一个结点，就将接待你放入栈中
            root = root->left;//继续遍历下一个左孩子结点
        }
        TNode node = popStack(&stack);//经过前面循环，左子树全部走完，接着走右子树
        printf("%c", node->element);//打印当前结点元素值
        root = node->right; //得到右孩子，重复上面的操作。
        // 如果没有右孩子，这里的 root 就被赋值为 NULL，下一轮循环直接跳过上面的 while，继续出站下一个结点找右子树
    }
}
源代码
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef char E;
typedef struct TreeNode {
    E element;
    struct TreeNode *left, *right;
} TreeNode, *TNode;

typedef TNode T;        //这里栈内元素类型定义为上面Node，也是二叉树结点指针
typedef struct StackNode {
    T element;
    struct StackNode *next;
} StackNode, *SNode;

//非递归操作
void initStack(SNode head) {
    head->next = NULL;
}

bool pushStack(SNode head, T element) {
    SNode node = malloc(sizeof(StackNode));
    if (node == NULL) return 0;
    node->element = element;
    node->next = head->next;
    head->next = node;
    return 1;
}

bool isEmpty(SNode head) {
    return head->next == NULL;
}

T popStack(SNode head) {
    SNode top = head->next;
    T e = head->next->element;
    head->next = head->next->next;
    free(top);
    return e;
}

void perOrder(TNode root) {
    StackNode stack;
    initStack(&stack);
    while (root || !isEmpty(&stack)) {       //栈为空且结点为 NULL 终止循环条件
        while (root) {          //先不断遍历左子树，直到没有为止
            printf("%c", root->element);    //打印当前结点元素值
            pushStack(&stack, root);    //每经过一个结点，就将接待你放入栈中
            root = root->left;      //继续遍历下一个左孩子结点
        }
        TNode node = popStack(&stack);    //经过前面循环，左子树全部走完，接着走右子树
        root = node->right; //得到右孩子，重复上面的操作。
        // 如果没有右孩子，这里的 root 就被赋值为 NULL，下一轮循环直接跳过上面的 while，继续出站下一个结点找右子树
    }
}

void inOrder(TNode root){
    StackNode stack;
    initStack(&stack);
    while (root || !isEmpty(&stack)) {//栈为空且结点为 NULL 终止循环条件
        while (root) {//先不断遍历左子树，直到没有为止
            pushStack(&stack, root);//每经过一个结点，就将接待你放入栈中
            root = root->left;//继续遍历下一个左孩子结点
        }
        TNode node = popStack(&stack);//经过前面循环，左子树全部走完，接着走右子树
        printf("%c", node->element);//打印当前结点元素值
        root = node->right; //得到右孩子，重复上面的操作。
        // 如果没有右孩子，这里的 root 就被赋值为 NULL，下一轮循环直接跳过上面的 while，继续出站下一个结点找右子树
    }
}

int main() {
    TNode a = malloc(sizeof(TreeNode));
    TNode b = malloc(sizeof(TreeNode));
    TNode c = malloc(sizeof(TreeNode));
    TNode d = malloc(sizeof(TreeNode));
    TNode e = malloc(sizeof(TreeNode));
    TNode f = malloc(sizeof(TreeNode));
    a->element = 'A';
    b->element = 'B';
    c->element = 'C';
    d->element = 'D';
    e->element = 'E';
    f->element = 'F';

    a->left = b;
    a->right = c;
    b->left = d;
    b->right = e;
    c->right = f;
    c->left = NULL;
    d->left = d->right = NULL;
    e->left = e->right = NULL;
    f->left = f->right = NULL;

    perOrder(a);
    printf("\n");
    inOrder(a);
}

image-20230820110011129

注：源代码部分均可以运行，复制粘贴即可。

线索二叉树

目的：引入线索二叉树正是为了加快查找结点前驱和后继的速度。

普通二叉树如何查找前驱和后继结点呢？

  1. 确定需要找到的结点p。
  2. 申请两个结点q和pre，首先q指向第一个结点，而pre指向null，然后遍历二叉树，q指向下一个结点（根据先序、中序和后续的顺序），pre指向q刚刚指向的结点。如此循环往复，直到q指向p
  3. 当p和q指针重合时，pre指向p的前驱结点。当pre和p指针重合时，q指向p的后继结点。

实质上还是二叉树的遍历。当一个操作中需要反复寻找某个结点的前驱或者后继时，这样的操作明显效率比较低。因此我们需要一种可以加快查找结点前驱和后继的速度的方法，从而引入了线索二叉树。

二叉链表

typedef int Element;
//二叉树的结点（链式存储）
typedef struct BiTNode {
    Element data;
    struct BiTNode *lchild, *rchild;
} BiTNode, *BiTNode;

线索链表

typedef int Element;
//线索二叉树结点
typedef struct ThreadNode {
    Element data;
    struct BiTNode *lchild, *rchild;
    int ltag, rtag;     //左、右线索标志
} ThreadNode, *ThreadTree;

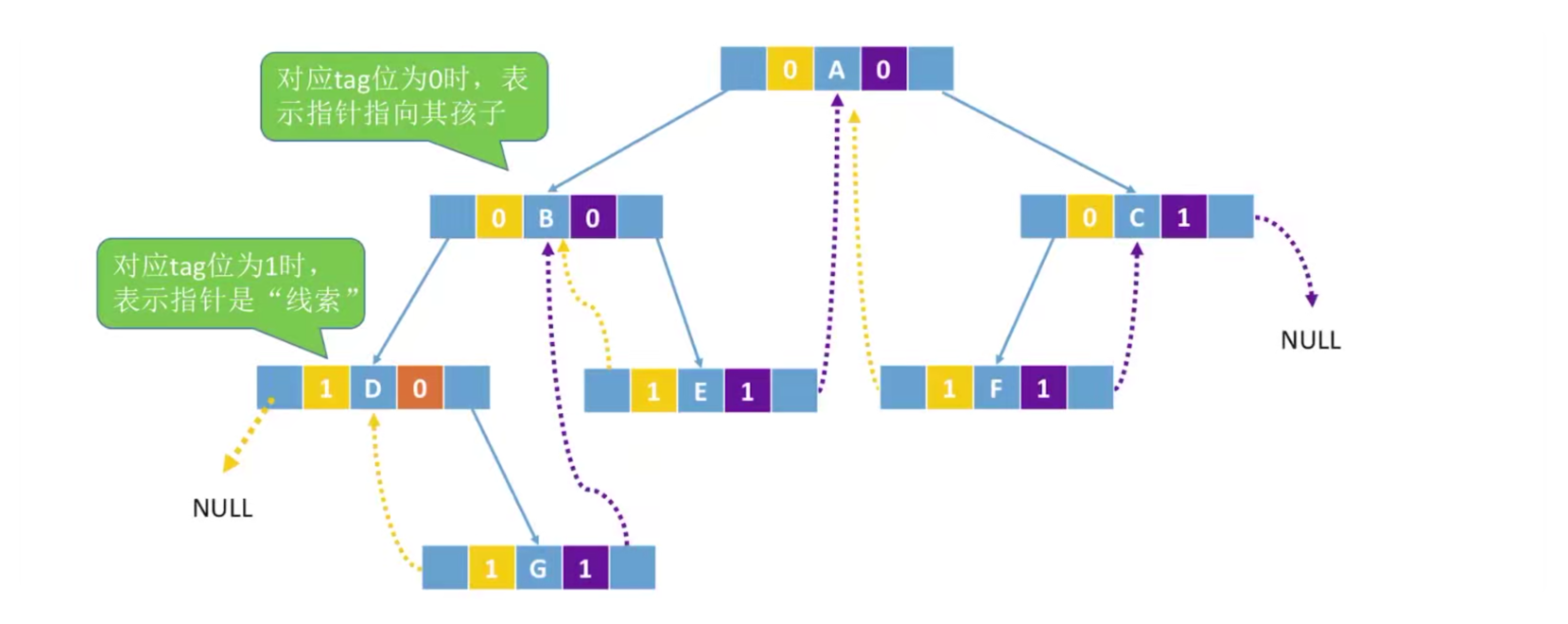
tag == 0：表示指针指向孩子

Tag == 1：表示指针是“线索”

中序线索二叉树的存储

image-20231020154713689

二叉树的线索化

王道教材版本

//中序线索化
void InThread(ThreadTree p, ThreadTree &pre){
    if(p != NULL){
        InThread(p->lchild, pre);     //递归，线索化左子树
        if(p->lchild == NULL){
            p->lchild = pre;
            p->ltag = 1;
        }
        if(pre != NULL && pre->rchild == NULL){
            pre->rchild = p;
            pre->rtag = 1;
        }
        pre = p;
        InThread(p->rchild, pre);
    }
}

//中序线索化二叉树T
void CreateInThread(ThreadTree T){
    ThreadTree pre = NULL;
    if(T != NULL){          //非空二叉树，线索化
        InThread(T, pre);     //线索二叉树
        pre->rchild = NULL; //处理遍历的最后一个结点
        pre->rtag = 1;
    }
}

课程版本

//中序线索化

typedef char Element;
//线索二叉树结点
typedef struct ThreadNode {
    Element data;
    struct ThreadNode *lchild, *rchild;
    int ltag, rtag;
} ThreadNode, *ThreadTree;

//全局变量 pre，指向当前访问结点的前驱
ThreadNode *pre = NULL;

void visit(ThreadNode *q) {
    if (q->lchild == NULL) { //左子树为空，建立前驱线索
        q->lchild = pre;
        q->ltag = 1;
    }
    if (pre != NULL && pre->rchild == NULL) {
        pre->rchild = q;    //建立前驱结点的后继线索
        pre->rtag = 1;
    }
    pre = q;
}

void  InThread(ThreadTree T){
    if(T != NULL){
        InThread(T->lchild);        //中序遍历左子树
        visit(T);                   //访问根结点
        InThread(T->rchild);        //中序遍历右子树
    }
}

void CreateInThread(ThreadTree T){
    pre = NULL;                 //pre初始为NULL
    if(T != NULL){              //非空二叉树才能线索化
        InThread(T);            //中序线索化二叉树
        if (pre->rchild == NULL){
            pre->rtag = 1;      //处理遍历的最后一个结点
        }
    }
}

线索二叉树 找前驱/后继

树和森林

树的存储

  1. 双亲表示法

    这种结构采用一组连续空间来存储每个结点，同时在每个结点中增设一个伪指针，指示其双亲结点在数组中的位置。

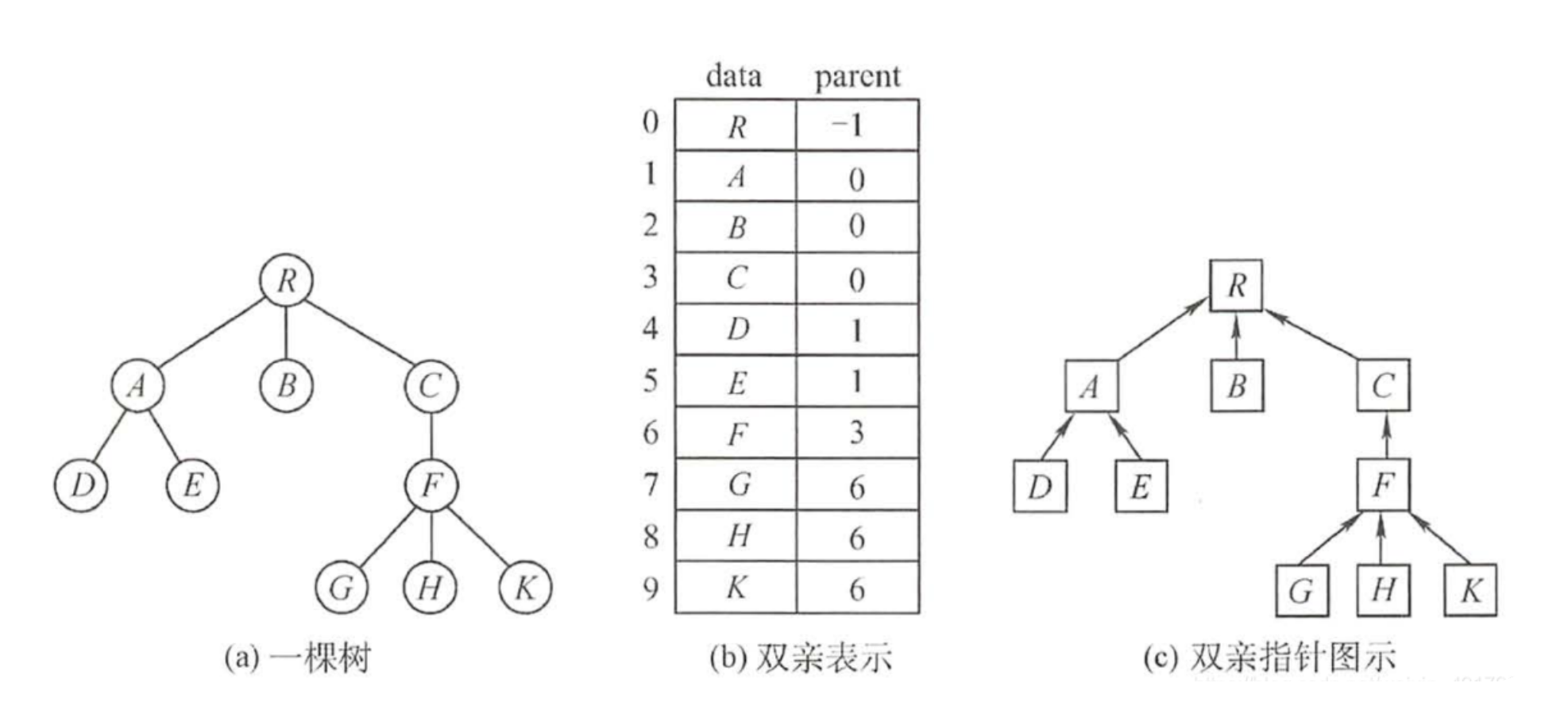
    image-20231023162730664

    双亲表示法的存储结构描述如下：

    #define MAX_TREE_SIZE 100      //树中最多结点数
typedef int element;

typedef struct {        //树的结点定义
    element data;       //数据元素
    int parent;         //双亲位置域
} PTNode;

typedef struct {        //树的类型定义
    PTNode nodes[MAX_TREE_SIZE];    //双亲表示
    int n;                          //结点数
} PTree;

    优点：可以很快地得每个结点的双亲结点。

    缺点：求结点的孩子时则需要遍历整个结构。

  2. 孩子表示法

    将每个结点的孩子结点都用单链表连接起来形成一个线性结构。

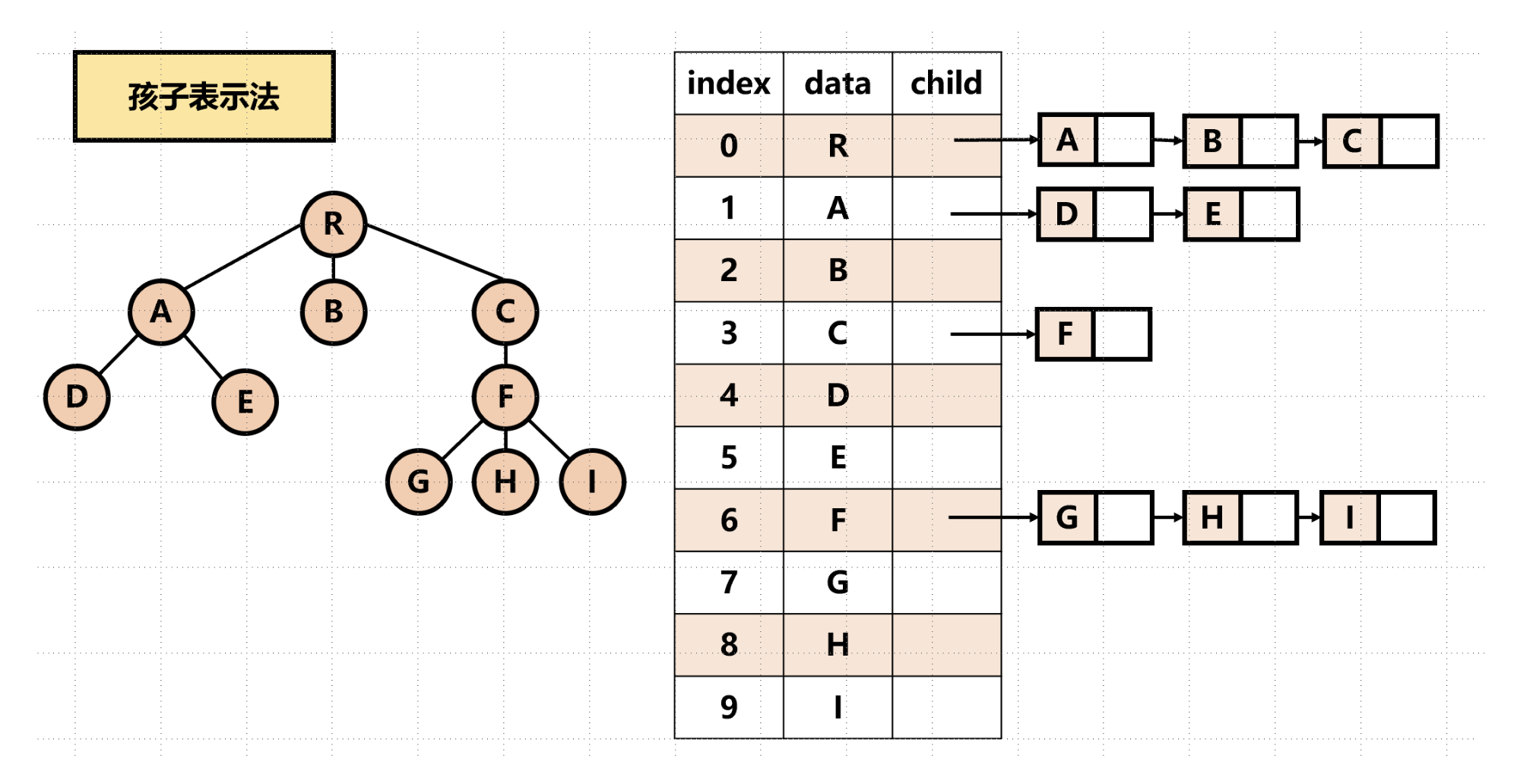
    image-20231023165045281

    优点：寻找子女的操作非常直接。

    缺点：寻找双亲的操作需要遍历n个结点中孩子链表指针域所指向的n个孩子链表。

  3. 孩子兄弟表示法

    即以二叉链表作为树的存储结构

树与二叉树的应用

哈夫曼树和哈夫曼编码

定义：树中结点常常被赋予一个表示某种意义的数值，称为该结点的权。从树到热一结点的路径长度与该结点上权值的乘积，称为该结点的带权路径长度。树中所有叶结点的带权路径长度之和称为该树的带权路径长度，记为
W P L = ∑ i = 1 n w i l i WPL= \sum_{i=1}^{n} w_i l_i WPL=i=1∑n​wi​li​
其中， w i w_i wi​表示第 i i i个叶结点所带的权值， l i l_i li​是该叶结点到根结点的路径长度。

哈夫曼树构造的特点：

  1. 每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大。
  2. 构造过程中共新建了 n − 1 n-1 n−1个结点（双分支结点），因此哈夫曼树的结点总数为 2 n − 1 2n-1 2n−1。
  3. 每次构造都选择 2 2 2棵树作为新结点的孩子，因此哈夫曼树中不存在度为 1 1 1的结点。

并查集

习题总结

⚠️判断完全二叉树 n 1 n_1 n1​的值 ⇔ n \Leftrightarrow n ⇔n
n 0 + n 1 + n 2 = 总结点 n n 1 = 0 / 1 n 0 = n 2 + 1 n_0 + n_1 + n_2 = 总结点n\\ n_1 = 0/1\\ n_0 = n_2 + 1 n0​+n1​+n2​=总结点nn1​=0/1n0​=n2​+1
由完全二叉树的性质可知，度为 1 的结点要么只有一个，要么就没有。

结合 n 0 = n 2 + 1 n_0 = n_2 + 1 n0​=n2​+1公式可知：如果 n 0 n_0 n0​为偶数 ⇒ n 2 \Rightarrow n_2 ⇒n2​为奇数；如果 n 0 n_0 n0​为奇数 ⇒ n 2 \Rightarrow n_2 ⇒n2​为偶数；所以 n 0 + n 2 n_0 + n_2 n0​+n2​一定为奇数。

用上面解释可知： n = n 0 + n 1 + n 2 n = n_0 + n_1 + n_2 n=n0​+n1​+n2​的奇偶性与 n 1 n_1 n1​有关。然而 n 1 = 0 / 1 n_1 = 0/1 n1​=0/1。

如果 n 1 = 0 n_1 = 0 n1​=0，那么 n n n为奇数；如果 n 1 = 1 n_1 = 1 n1​=1，那么 n n n为偶数；反之如果 n n n为偶数，那么 n 1 = 1 n_1 = 1 n1​=1；如果 n n n为奇数，那么 n 1 = 0 n_1 = 0 n1​=0。

e g : eg: eg:一棵完全二叉树上有 1001 个结点，其中叶结点的个数是 ( D ) (D) (D)

A . 250 A.250 A.250 B . 500 B.500 B.500 C . 254 C.254 C.254 D . 501 D.501 D.501

解： n = 1001 n = 1001 n=1001为奇数，则 n 1 = 0 n_1 = 0 n1​=0，那么 n = n 0 + n 1 + n 2 = n 0 + n 2 = n 0 + ( n 0 − 1 ) = 2 n 0 − 1 = 1001 n = n_0 + n_1 + n_2 = n_0 + n_2 = n_0 + (n_0 - 1) = 2n_0 - 1 = 1001 n=n0​+n1​+n2​=n0​+n2​=n0​+(n0​−1)=2n0​−1=1001，解得 n = 501 n = 501 n=501。

e g : eg: eg:【2016年全国试题】若森林F有15条边、25个结点，则F包含树的个数是 （ C ） （C） （C）

A . 8 A.8 A.8 B . 9 B.9 B.9 C . 10 C.10 C.10 D . 11 D.11 D.11

解：树的结点数n，边数（分支数）B有确定的关系 n = B + 1 n = B + 1 n=B+1，森林是不相交的树的集合，则森林的结点数 F n = ∑ T i = ∑ ( B i + 1 ) F_n = \sum T_i = \sum(B_i + 1) Fn​=∑Ti​=∑(Bi​+1)，其中 T i T_i Ti​就是森林中第 i i i棵树的结点数， B I B_I BI​是森林中第 i i i棵树的分支。设森林中有 m m m棵树，则 F n = ∑ B i + m F_n = \sum B_i + m Fn​=∑Bi​+m，即 25 = 15 + m 25 = 15 + m 25=15+m，即森林中有10棵树。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1129125.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

交换机基础（四）：MSTP负载均衡配置案例

交换机基础（四）：MSTP负载均衡配置案例

如图所示是某个企业内部核心网络的结构图&#xff0c;目前企业中有20个VLAN, 编号为VLAN1&#xff5e;VLAN20, 为了确保内部网络的可靠性&#xff0c;使用 了冗余链路和MSTP 协议。为了能更好地利用网络资源和带宽&#xff0c;现管理员希望通过配置MSTP 的负载均衡实现网络带宽…
阅读更多...
【proteus】8086 写一个汇编程序并调试

【proteus】8086 写一个汇编程序并调试

参考书籍&#xff1a;微机原理与接口技术——基于8086和Proteus仿真&#xff08;第3版&#xff09;p103-105&#xff0c;p119-122. 参考程序是p70&#xff0c;例4-1 在上一篇的基础上&#xff1a; 创建项目和汇编文件 写一个汇编程序并编译 双击8086的元件图&#xff1a; …
阅读更多...
2.1 向量与线性方程组

2.1 向量与线性方程组

一、行图像与列图像 线性代数的中心问题是求解线性方程组。线性的意思是这些方程的未知数是一次的&#xff0c;即每个未知数只会乘数字&#xff0c;而不会出现 x x x 与 y y y 相乘的项。下面是一个由两个未知数组成的方程组&#xff1a; 两个方程 两个未知数 { x − 2 y 1…
阅读更多...
Django学习笔记——文件上传（界面还怪好看得嘞）

Django学习笔记——文件上传（界面还怪好看得嘞）

定义文件上传函数 #文件上页面 def uploadFileIndex(request):return render(request, "uploadFile.html")#文件上传接口 def uploadFile(request):if request.method POST and request.FILES[file]:uploaded_file request.FILES[file]fs FileSystemStorage()# 选…
阅读更多...
螺旋矩阵[中等]

螺旋矩阵[中等]

优质博文&#xff1a;IT-BLOG-CN 一、题目 给你一个m行n列的矩阵matrix&#xff0c;请按照顺时针螺旋顺序&#xff0c;返回矩阵中的所有元素。 示例 1&#xff1a; 输入&#xff1a;matrix [[1,2,3],[4,5,6],[7,8,9]] 输出&#xff1a;[1,2,3,6,9,8,7,4,5] 示例 2&#xf…
阅读更多...
vue如何使用冻结对象提升代码效率及其原理解析

vue如何使用冻结对象提升代码效率及其原理解析

先给大家伙整个实际工作中一定会碰到的问题 如下vue dome ,它的代码非常简单功能也1非常简单,就是一个按钮,点击后会显示有多少条数据 来看看源码, html部分就是一个按钮绑定了一个loadData事件,然后在p标签内展示了这个myData这个数据的长度 <template><div id&quo…
阅读更多...
Txt病毒

Txt病毒

一.txt病毒原理 利用翻转字符串的方法 混淆伪装 &#xff08;jpg 、doc、ppt 等&#xff09; &#xff08;1&#xff09;更改程序图标 &#xff08;2&#xff09;将程序重命名 readtxt.exe 鼠标放到 read 与 txt 中间 设置格式为 RLO // 这个“RLO”是一个转义字符&#xf…
阅读更多...
交互式 Web 应用 0 基础入门

交互式 Web 应用 0 基础入门

初探 Gradio&#xff1a;轻松构建交互式 Web 应用 文章目录 初探 Gradio&#xff1a;轻松构建交互式 Web 应用Why Gradio?安装 Gradio创建交互式界面1. gr.Interface2. gr.Blocks 强大的组件库输入输出组件控制组件布局组件 示例交互式数据可视化多组件同时&#xff08;嵌套&a…
阅读更多...
Netty框架详解

Netty框架详解

一、Netty简介 Netty是一款基于Java NIO的网络编程、高性能、异步事件驱动的网络应用框架。它的设计目标是提供简单易用、高性能、可扩展的网络编程框架。 二、Netty主要特点 高并发&#xff1a;Netty使用异步的、非阻塞的I/O模型&#xff0c;通过事件驱动的方式处理网络操作…
阅读更多...
回归预测 | MATLAB实现BO-LSTM贝叶斯优化长短期神经网络多输入单输出回归预测

回归预测 | MATLAB实现BO-LSTM贝叶斯优化长短期神经网络多输入单输出回归预测

回归预测 | MATLAB实现BO-LSTM贝叶斯优化长短期神经网络多输入单输出回归预测 目录 回归预测 | MATLAB实现BO-LSTM贝叶斯优化长短期神经网络多输入单输出回归预测效果一览基本介绍模型搭建程序设计参考资料 效果一览 基本介绍 MATLAB实现BO-LSTM贝叶斯优化长短期神经网络多输入…
阅读更多...
潮流玩具演绎城市文化，泡泡玛特入选2023“上海礼物”

潮流玩具演绎城市文化，泡泡玛特入选2023“上海礼物”

每一座城市都有其独特的文化氛围和历史背景&#xff0c;“城市礼物”承载着地域特色、文化内涵和人文精神&#xff0c;不断复制和传递着城市文化。近年来&#xff0c;上海市文旅局会同有关各方&#xff0c;从旅游商品的研发设计、品牌塑造、展售渠道等方面&#xff0c;创建“上…
阅读更多...
【软件教程】如何用C++交叉编译出能在Android运行的ELF程序或so动态库

【软件教程】如何用C++交叉编译出能在Android运行的ELF程序或so动态库

一、配置NDK交叉编译平台 1. 打开Android的官方ndk下载链接https://developer.android.com/ndk/downloads?hlzh-cn&#xff0c;下载windows 64位ndk环境包。 2. 解压后将具有以下文件的路径加入到系统环境变量。 3. 配置好环境变量&#xff0c;如下图所示&#xff0c;Path中存…
阅读更多...
mysql 数据库 表结构生成word文档

mysql 数据库 表结构生成word文档

1、背景 我们在做项目时&#xff0c;表设计文档都是非常重要的&#xff0c;可以让开发人员快速了解表与业务的关系、表之间的关系。 产品在不停迭代的过程中&#xff0c;表的结构也会有相应的变化&#xff0c;我们需要将变化更新的表设计文档中。以前我们是人工方式更新文档&…
阅读更多...
C++ 虚函数详解：多态性实现原理及其在面向对象编程中的应用

C++ 虚函数详解：多态性实现原理及其在面向对象编程中的应用

在面向对象的编程中&#xff0c;多态性是一个非常重要的概念。多态性意味着在不同的上下文中使用同一对象时&#xff0c;可以产生不同的行为。C是一种面向对象的编程语言&#xff0c;在C中&#xff0c;虚函数是实现多态性的关键 什么是虚函数 虚函数是一个在基类中声明的函数&…
阅读更多...
基于SpringBoot的时间管理系统

基于SpringBoot的时间管理系统

基于SpringBoot的时间管理系统的设计与实现~ 开发语言&#xff1a;Java数据库&#xff1a;MySQL技术&#xff1a;SpringBootMyBatis工具&#xff1a;IDEA/Ecilpse、Navicat、Maven 系统展示 登录界面 管理员界面 用户界面 摘要 基于Spring Boot的时间管理系统是一款功能丰富…
阅读更多...
【Redis安装】Ubuntu和Centos

【Redis安装】Ubuntu和Centos

此处安装的是 Redis5 在 Ubuntu 系统上 切换到 root 用户下&#xff0c;su 命令切换使用 apt 可以搜索 redis 相关软件包 apt search redis使用 apt 命令安装 redis apt install redis手动修改配置文件 redis.conf cd /etc/redis/ vim redis.conf修改以下两处 重启服务器 …
阅读更多...
2021年下半年 软件设计师 上午试卷（1-28）

2021年下半年 软件设计师 上午试卷（1-28）

计算机指令系统采用多种寻址方式。立即寻址是指操作数包含在指令中&#xff0c;寄存器寻址是指操作数在寄存器中&#xff0c;直接寻址是指操作数的地址在指令中。这三种寻址方式获取操作数的速度 &#xff08;1&#xff09; 。 &#xff08;1&#xff09; A. 立即寻址最快&am…
阅读更多...
【JAVA学习笔记】43 - 枚举类

【JAVA学习笔记】43 - 枚举类

项目代码 https://github.com/yinhai1114/Java_Learning_Code/tree/main/IDEA_Chapter11/src/com/yinhai/enum_ 〇、创建时自动填入版权 作者等信息 如何在每个文件创建的时候打入自己的信息以及版权呢 菜单栏-File-setting-Editor-File and Code Templaters -Includes-输入信…
阅读更多...
SpringBoot整合Activiti7——任务监听器（七）

SpringBoot整合Activiti7——任务监听器（七）

文章目录 一、任务监听器事件类型配置方式(选)代码实现xml文件创建监听器class方式expression方式delegateExpression 测试流程部署流程启动流程完成任务 一、任务监听器 任务监听器可以在任务创建、任务分配、任务完成、任务删除发生时触发&#xff0c;从而执行相应的逻辑。 事…
阅读更多...
rust学习——方法 Method

rust学习——方法 Method

文章目录 方法 Method定义方法self、&self 和 &mut self方法名跟结构体字段名相同 带有多个参数的方法关联函数多个 impl 定义为枚举实现方法 rust 结构体与枚举的区别回答1回答2 方法 Method 从面向对象语言过来的同学对于方法肯定不陌生&#xff0c;class 里面就充斥…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023