螺旋矩阵[中等]

news2024/11/6 7:17:21

优质博文：IT-BLOG-CN

一、题目

给你一个m行n列的矩阵matrix，请按照顺时针螺旋顺序，返回矩阵中的所有元素。

示例 1：

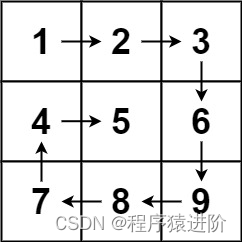
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

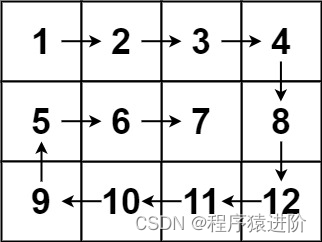
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

二、代码

【1】模拟： 由于是旋转矩阵，所以我们创建一个旋转二维坐标 int[][] coordinate = { {0,1},{1,0},{0,-1},{-1,0} }，第一次旋转前row + 0, column + 1，所以取coordinate[0]，第一次旋转后row + 1, column + 0所以取coordinate[1]依次类推。判断路径是否进入之前访问过的位置需要使用一个与输入矩阵大小相同的辅助矩阵visiters，其中的每个元素表示该位置是否被访问过。当一个元素被访问时，将visited中的对应位置的元素设为已访问。

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        //思路： 1、定义一个顺时针坐标 coordinate，进行下表的加减；
        //       2、创建一个大小相同的二位数组，表示是否访问过；
        //       3、当满足旋转条件时，获取顺序坐标，进行加减；
        
         List<Integer> res = new ArrayList();
        if (matrix.length == 0) {
            return res;
        }
        // 获取矩阵的行和列
        int rows = matrix.length, columns = matrix[0].length;
        // 坐标
        int[][] coordinate = {{0,1},{1,0},{0,-1},{-1,0}};
        boolean[][] visiters = new boolean[rows][columns];

        // 获取总的旋转次数
        int total = rows * columns;
        // 定义一个坐标的小标，表示什么时候进行旋转，和行和列的下标；
        int coorIndex = 0, row = 0, column = 0;
        for (int i = 0; i < total; i++) {
            // 初始化第一个数据，并修改 visiters中的属性
            res.add(matrix[row][column]);
            visiters[row][column] = true;
            // 获取下一个row和column，并判断是否满足旋转条件
            int nextRow = coordinate[coorIndex][0] + row, nextColumn = coordinate[coorIndex][1] + column;
            if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visiters[nextRow][nextColumn]) {
                // 因为不止旋转依次，所以不能只+1
                coorIndex = (coorIndex + 1) % 4;
                nextRow = coordinate[coorIndex][0] + row;
                nextColumn = coordinate[coorIndex][1] + column;
            }
            row = nextRow;
            column = nextColumn;
        }
        return res;
    }
}

时间复杂度： O(mn)其中m和n分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。
空间复杂度： O(mn)需要创建一个大小为m×n的矩阵visited记录每个位置是否被访问过。

【2】按层模拟： 可以将矩阵看成若干层，首先输出最外层的元素，其次输出次外层的元素，直到输出最内层的元素。定义矩阵的第k层是到最近边界距离为k的所有顶点。例如，下图矩阵最外层元素都是第1层，次外层元素都是第2层，剩下的元素都是第3层。

[[1, 1, 1, 1, 1, 1, 1],
 [1, 2, 2, 2, 2, 2, 1],
 [1, 2, 3, 3, 3, 2, 1],
 [1, 2, 2, 2, 2, 2, 1],
 [1, 1, 1, 1, 1, 1, 1]]

对于每层，从左上方开始以顺时针的顺序遍历所有元素。假设当前层的左上角位于(top,left)，右下角位于(bottom,right)，按照如下顺序遍历当前层的元素。
【1】从左到右遍历上侧元素，依次为(top,left)到(top,right)。
【2】从上到下遍历右侧元素，依次为(top+1,right)到(bottom,right)。
【3】如果left<right且top<bottom，则从右到左遍历下侧元素，依次为(bottom,right−1)到(bottom,left+1)，以及从下到上遍历左侧元素，依次为(bottom,left)到(top+1,left)。

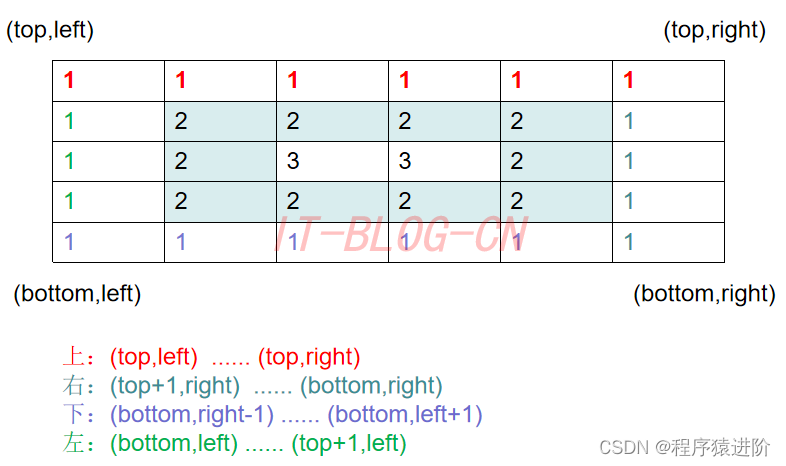
遍历完当前层的元素之后，将left和top分别增加1，将right和bottom分别减少1，进入下一层继续遍历，直到遍历完所有元素为止。

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return order;
        }
        int rows = matrix.length, columns = matrix[0].length;
        int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
        while (left <= right && top <= bottom) {
            for (int column = left; column <= right; column++) {
                order.add(matrix[top][column]);
            }
            for (int row = top + 1; row <= bottom; row++) {
                order.add(matrix[row][right]);
            }
            if (left < right && top < bottom) {
                for (int column = right - 1; column > left; column--) {
                    order.add(matrix[bottom][column]);
                }
                for (int row = bottom; row > top; row--) {
                    order.add(matrix[row][left]);
                }
            }
            left++;
            right--;
            top++;
            bottom--;
        }
        return order;
    }
}