题目
51. N 皇后
困难
相关标签
数组 回溯
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
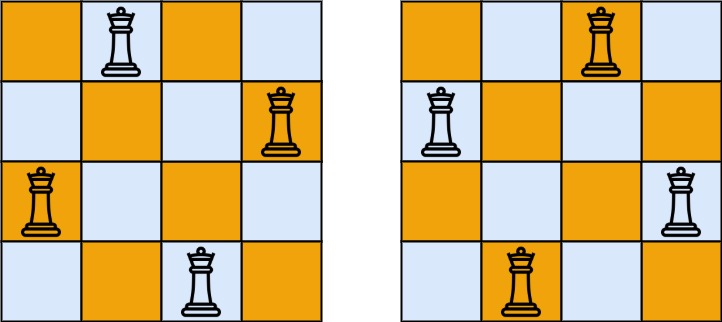
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:[["Q"]]
提示:
1 <= n <= 9
思路和解题方法
首先,定义了一个名为 Solution 的类。其中:
- ans:成员变量,用于记录所有可行的 N 皇后方案;
- backtracking:回溯函数,用来尝试放置 N 个皇后;
- isvalid:函数,用于检查当前位置是否可放置皇后;
- solveNQueens:主函数,使用回溯法求解 N 皇后问题。
在 backtracking 函数中:
- 当已经成功放置 N 个皇后时,将当前的棋盘加入答案数组 ans 中。
- 对于每一行,在第 col 列尝试放置皇后,如果该格子可行,则标记上皇后,继续向下一行进行搜索,搜索完后回溯到上一步位置并取消标记;
- 搜索过程中,调用函数 isvalid 进行当前位置是否可放的判断。
在 isvalid 函数中:
- 检查当前列是否已经有皇后;
- 检查左上方是否已经有皇后;
- 检查右上方是否已经有皇后;
- 如果以上均未出现皇后,则说明该位置可放置皇后,返回真。
而在主函数 solveNQueens 中:
- 清空答案数组 ans,并定义初始棋盘状态 chessboard;
- 调用回溯函数 backtracking 在 chessboard 中查找所有可行的 N 皇后方案;
- 返回答案数组 ans。
复杂度
时间复杂度:
O(n!)
算法的时间复杂度为 O(n!),其中 n 表示棋盘大小。因为每一行只能放置一个皇后,所以在搜索下一行的时候,需要排除已经放置的皇后所在的列和两条对角线上的位置,因此每一行可选的位置数是 n,总的搜索次数是 n×(n−2)×(n−4)×⋯1=n!。
空间复杂度
O(n^2)
算法的空间复杂度是 O(n2),因为需要使用一个 n×n 的二维数组
chessboard来存储棋盘状态,同时还需要使用一个二维数组ans来存储所有可行的 N 皇后方案。
c++ 代码
class Solution {
public:
vector<vector<string>> ans; // 存储所有可行的 N 皇后方案
void backtracking(int n, int row, vector<string> &chessboard)
{
if (row == n) // 若已成功放置 N 个皇后,将当前棋盘加入答案数组
{
ans.push_back(chessboard);
return;
}
for (int col = 0; col < n; col++) // 在当前行的每一列尝试放置皇后
{
if (isvalid(row, col, chessboard, n)) // 若当前位置可放置皇后
{
chessboard[row][col] = 'Q'; // 放置皇后
backtracking(n, row + 1, chessboard); // 继续下一行的搜索
chessboard[row][col] = '.'; // 回溯到上一步,取消该位置的皇后标记
}
}
}
bool isvalid(int row, int col, vector<string> &chessboard, int n)
{
for (int i = 0; i < row; i++)
{
if (chessboard[i][col] == 'Q') // 检查当前列是否已经有皇后
return false;
}
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--)
{
if (chessboard[i][j] == 'Q') // 检查左上方是否已经有皇后
return false;
}
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++)
{
if (chessboard[i][j] == 'Q') // 检查右上方是否已经有皇后
return false;
}
return true; // 当前位置可放置皇后
}
vector<vector<string>> solveNQueens(int n) {
ans.clear(); // 清空答案数组
vector<string> chessboard(n, string(n, '.')); // 初始化棋盘
backtracking(n, 0, chessboard); // 调用回溯函数开始搜索
return ans; // 返回所有可行的 N 皇后方案
}
};
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。