文章目录
- 对偶问题的解
- 影子价格
- 对偶价格
- 对偶价格与影子价格的关系
- 总结
- 例题
对偶问题的解

影子价格
影子价格是一个经济学意义上的解释,因为不同的解读,目前对于影子价格准确的定义较为混乱。下面下来举几个例子:
- the shadow price associated with a resource tells you how much more profit you would get by increasing the amount of that resource by one unit. (So “How much you would be willing to pay for an additional resource” is a good way of thinking about the shadow price.)(与某一资源相关的影子价格告诉我们,增加一个单位的资源量会增加多少利润。(因此,"你愿意为增加一个资源单位支付多少钱 "是一种很好的影子价格思维方式)。
link:https://math.stackexchange.com/questions/91504/shadow-prices-in-linear-programming - Basically, a shadow price is an estimated cost for a good or service that isn’t typically offered for sale or priced in the market. In more detail, a shadow price is The increase in value (often increased contribution) resulting from having one more unit of a limited resource accessible at its original cost can be used to determine a resource’s shadow price. Since there is existing slack, non-critical restrictions will have zero shadow pricing. In economics, the “Shadow price” is a substitute value for an item or service without a market price. It is what someone must give up to obtain an additional unit. If the beneficiaries’ preferences are known, the shadow price can help assess the costs or advantages of a project. The shadow price for each constraint, the amount the objective function will change given one additional unit on the right-hand side (RHS) of the constraint and no other modifications, is calculated using Excel or linear programming. By deducting the original objective function value from the objective function value with one extra unit of the resource on the RHS, the shadow price value can likewise be calculated.
(影子价格是一种商品或服务的估计成本,通常不在市场上出售或定价。
更详细地说,影子价格是指以原始成本多获得一个单位的有限资源所带来的价值增加(通常是贡献增加),可用于确定资源的影子价格。
由于存在闲置,非关键限制的影子价格为零。
**在经济学中,"影子价格 "是没有市场价格的物品或服务的替代价值。**它是某人为获得额外单位而必须放弃的东西。如果知道受益人的偏好,影子价格可以帮助评估项目的成本或优势。
每个约束条件的影子价格,即在约束条件右侧(RHS)增加一个单位且不做其他修改的情况下,目标函数的变化量,可通过Excel或线性规划来计算。通过从RHS上增加一个单位资源的目标函数值中减去原来的目标函数值,同样可以计算出影子价格值。)
link:https://www.codingdeeply.com/how-to-calculate-dual-price-in-linear-programming/?expand_article=1
对偶价格
- The dual price indicates the cost of achieving the last unit of the minimum production goal in the event of a greater-than-or-equal restriction, such as a minimum production level constraint. (对偶价格表示在大于或等于限制(如最低生产水平限制)的情况下,实现最低生产目标最后一个单位的成本)
link:https://www.codingdeeply.com/how-to-calculate-dual-price-in-linear-programming/?expand_article=1
对偶价格与影子价格的关系

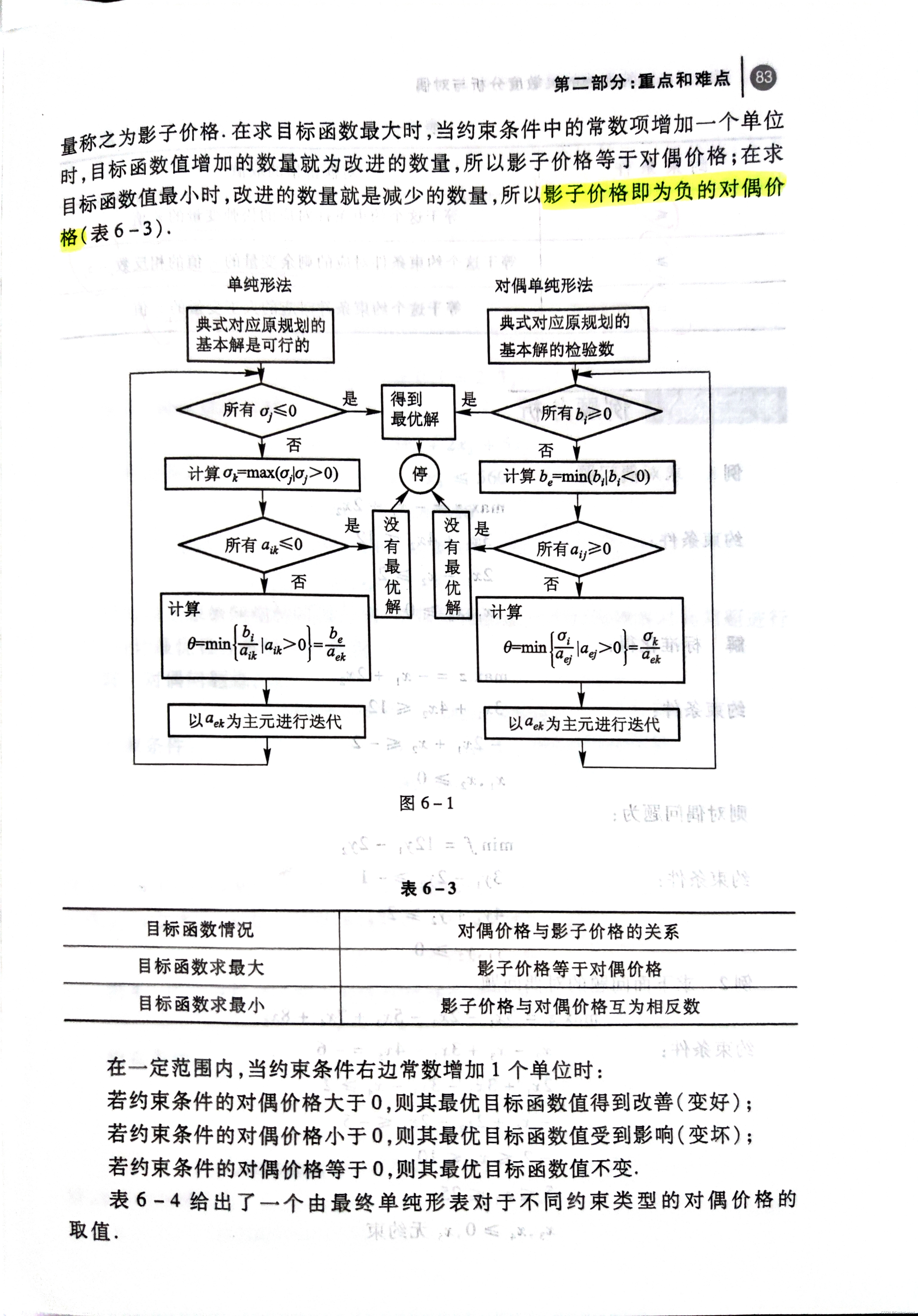
2.
3. 清华大学出版社:《运筹学》
- 影子价格反映资源对目标价格的边际贡献

总结
综上,将对偶价格dual price定义为:当约束条件中的常数项增加一个单位时,最优目标函数值变化的数量。
将影子价格shadow price定义为:当约束条件中的常数项增加一个单位时,最优目标函数值增加的数量。
变化的数量可以理解为不带符号的,只有大小。
增加的数量可以理解为带符号的,有方向。
此时的对偶价格和对偶问题的解是相等的。而影子价格可能是对偶问题的解的负数。
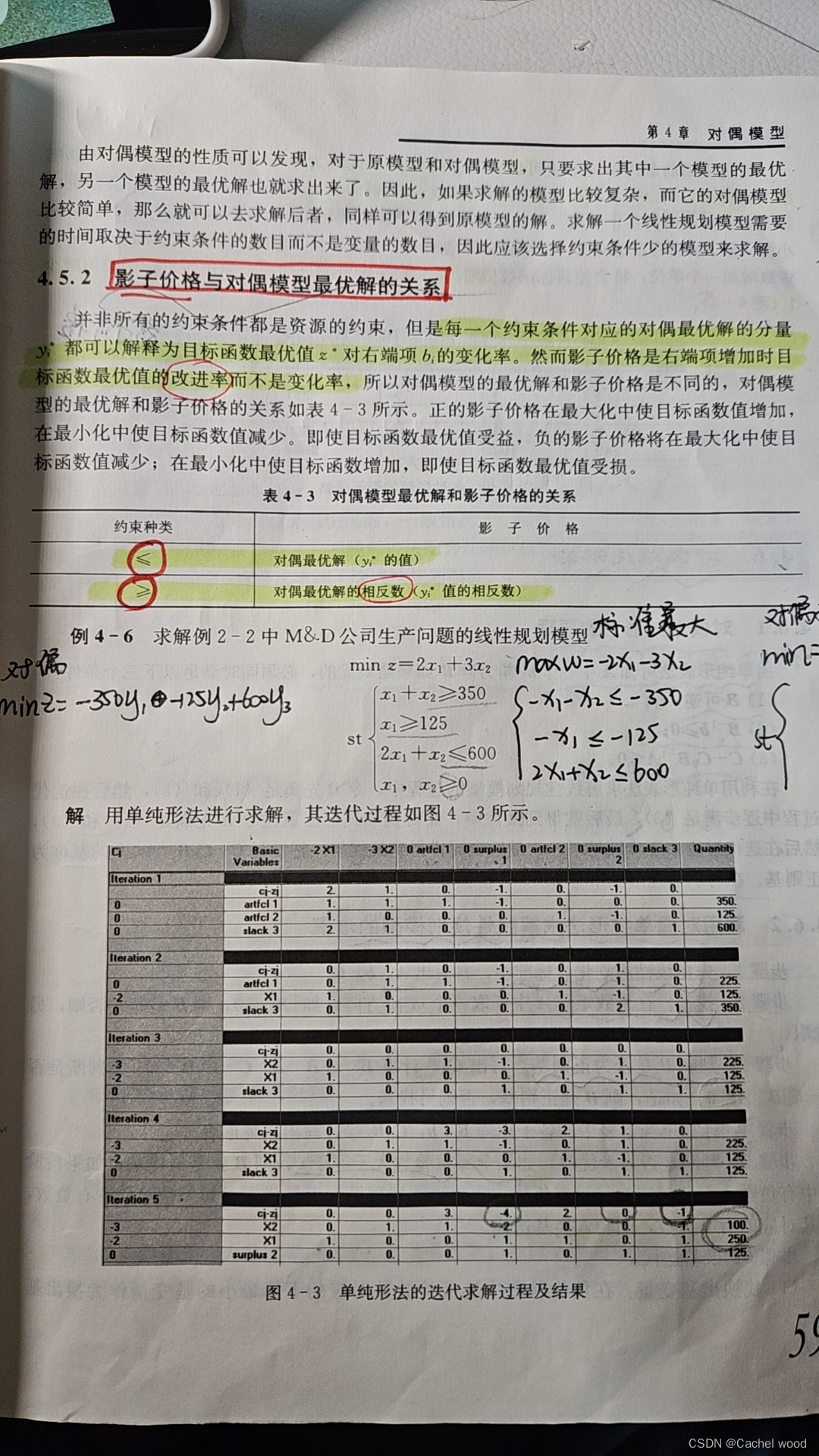
例题

对偶问题的解:根据
−
y
=
0
−
c
B
B
−
1
=
σ
i
-y = 0 - c_BB^{-1} = \sigma_i
−y=0−cBB−1=σi,所以对偶问题的解为
y
∗
=
−
σ
i
,
3
,
1
y^{*}=-\sigma_i,3,1
y∗=−σi,3,1,
对偶价格:与对偶问题的解相同,
3
,
1
3,1
3,1
影子价格:对最大化问题, 且约束条件均为 ”小于等于“,影子价格等于对偶问题的解。
3
,
1
3,1
3,1


-
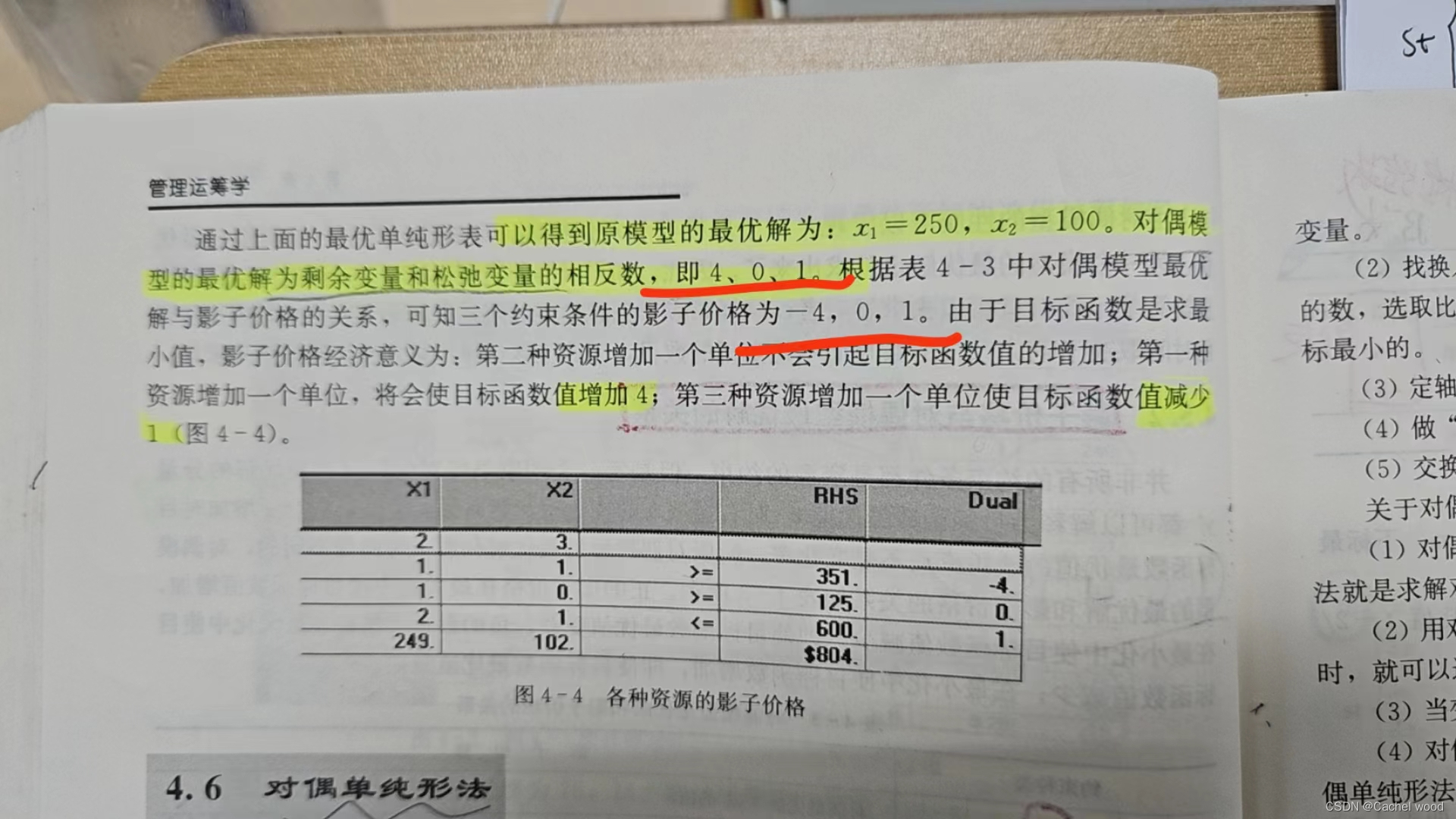
对偶问题的解:根据 − y = 0 − c B B − 1 = σ i -y = 0 - c_BB^{-1} = \sigma_i −y=0−cBB−1=σi,所以对偶问题的解为 y ∗ = − σ i , 4 , 0 , 1 y^{*}=-\sigma_i,4,0,1 y∗=−σi,4,0,1,
-
对偶价格:与对偶问题的解相同, 4 , 0 , 1 4,0,1 4,0,1
-
影子价格:对最大化问题,当约束条件中的常数项增加一个单位时,最优目标函数值增加的数量和改变的数量相同。
但是本题目是最小化问题,当约束条件中的常数项增加一个单位时,最优目标函数值增加的数量和改变的数量相反。
因为对最小化问题而言,此时模型可以继续向最优化(最小化)迭代,此时增加的数量则是负数。 -
影子价格:对最小化问题, 对约束条件为 ”小于等于“(3),影子价格等于对偶问题的解,约束条件为”大于等于“的(1)(2),影子价格等于对偶问题的解的相反数。 − 4 , 0 , 1 -4,0,1 −4,0,1