动态规划：13目标和

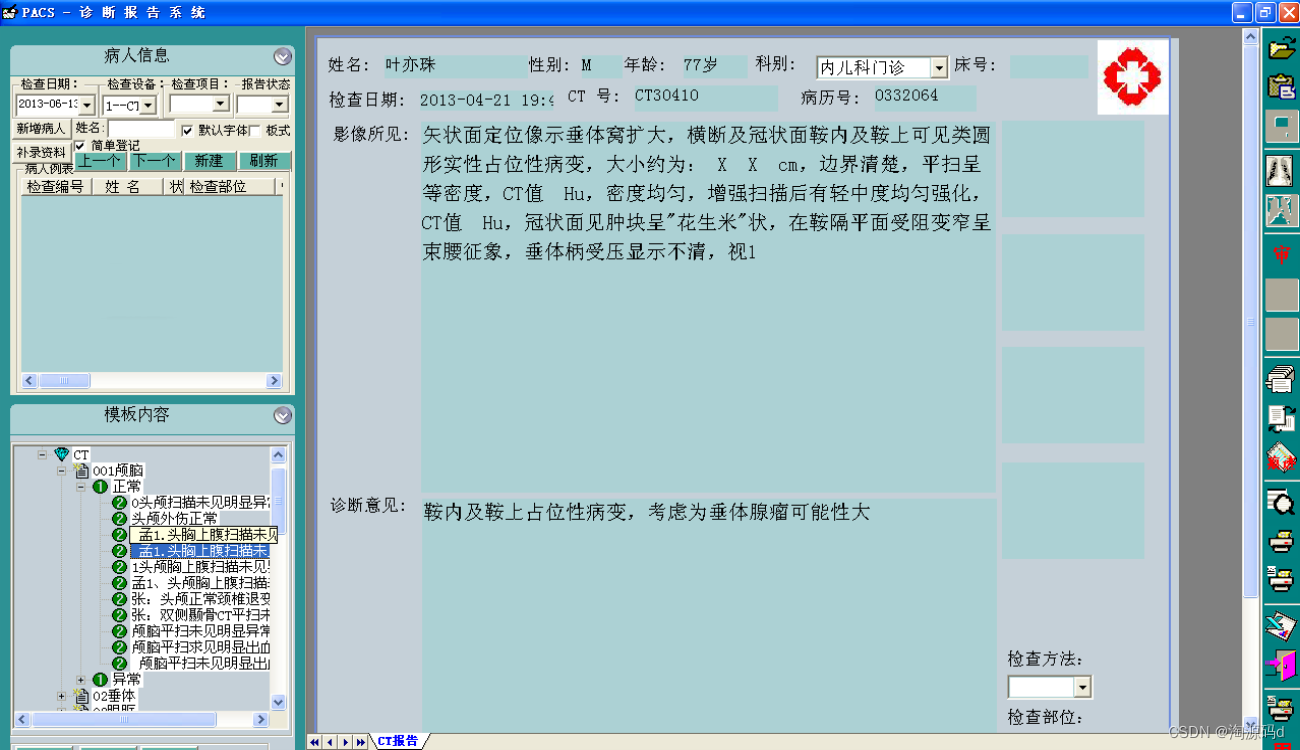
题目：494. 目标和

---

如何转化为01背包问题呢。

假设加法的总和为x，那么减法对应的总和就是sum - x。

所以我们要求的是 x - (sum - x) = target

x = (target + sum) / 2

此时问题就转化为，装满容量为x的背包，有几种方法。

这里的x，就是bagSize，也就是我们后面要求的背包容量。

大家看到(target + sum) / 2 应该担心计算的过程中向下取整有没有影响。

这么担心就对了，例如sum 是5，target是2的话其实就是无解的，所以：

if ((target + sum) % 2 == 1) return 0; // 此时没有方案

同时如果 target的绝对值已经大于sum，那么也是没有方案的。

if (Math.abs(target) > sum) return 0; // 此时没有方案

再回归到01背包问题，为什么是01背包呢？

因为每个物品（题目中的1）只用一次！

这次和之前遇到的背包问题不一样了，之前都是求容量为j的背包，最多能装多少。

本题则是装满有几种方法。其实这就是一个组合问题了。

五部曲

1. 确定dp数组含义：填满j（包括j）这么大容积的包，有dp[j]种方法

2. 确定递归公式：dp[j] += dp[j - nums[i]]

   有哪些来源可以推出dp[j]呢？

   只要搞到nums[i]，凑成dp[j]就有dp[j - nums[i]] 种方法。

   例如：dp[j]，j 为5，

   • 已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 容量为5的背包。
   • 已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 容量为5的背包。
   • 已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 容量为5的背包
   • 已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 容量为5的背包
   • 已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 容量为5的背包

   那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。

   所以求组合类问题的公式，都是类似这种：

   dp[j] += dp[j - nums[i]]
   

   这个公式在后面在讲解背包解决排列组合问题的时候还会用到！

3. dp数组初始化：dp[0] = 1

   从递推公式可以看出，在初始化的时候dp[0] 一定要初始化为1，因为dp[0]是在公式中一切递推结果的起源，如果dp[0]是0的话，递推结果将都是0。

   这里有人可能认为从dp数组定义来说 dp[0] 应该是0，也有人认为dp[0]应该是1。

   其实不要硬去解释它的含义，咱就把 dp[0]的情况带入本题看看应该等于多少。

   如果数组[0] ，target = 0，那么 bagSize = (target + sum) / 2 = 0。 dp[0]也应该是1， 也就是说给数组里的元素 0 前面无论放加法还是减法，都是 1 种方法。(我们注意到一点，之前的题目物品的重量都不会为0，但是本题中是可以为0的，物品重量既然为0了，那么我们容量为0的背包就可以装重量为0的物品，所以特殊)

   所以本题我们应该初始化 dp[0] 为 1。

   可能有同学想了，那 如果是 数组[0,0,0,0,0] target = 0 呢。

   其实 此时最终的dp[0] = 32，也就是这五个零 子集的所有组合情况，但此dp[0]非彼dp[0]，dp[0]能算出32，其基础是因为dp[0] = 1 累加起来的。

   dp[j]其他下标对应的数值也应该初始化为0，从递推公式也可以看出，dp[j]要保证是0的初始值，才能正确的由dp[j - nums[i]]推导出来。

4. 遍历顺序：先物后包，包要倒序

5. debug：打印dp数组

总结

本题还是有点难度，大家也可以记住，在求装满背包有几种方法的情况下，递推公式一般为：

dp[j] += dp[j - nums[i]];

后面我们在讲解完全背包的时候，还会用到这个递推公式！