文章目录
- 七、捷联惯导更新:insPropagation()
- 1、insPropagation():捷联惯导递推
- 2、imuCompensate():IMU数据误差补偿
- 3、insMech():IMU 状态更新(机械编排)
- 4、velUpdate():速度更新
- 1. 算法
- 2. 代码实现
- 5、posUpdate():位置更新
- 1. 算法
- 2. 代码实现
- 6、attUpdate():姿态更新
- 1. 算法
- 2. 代码实现
- 7、误差传播
- 八、GNSS 量测更新、系统状态反馈
- 1、gnssUpdate():GNSS 量测更新
- 2、EKFUpdate():EKF 更新协方差和误差状态
- 3、stateFeedback():状态反馈
- 九、KF-GINS常见问题
- KF-GINS能够达到怎么样的定位精度?
- 初始导航状态和初始导航状态标准差如何给定?
- IMU数据输入到程序之前,需要扣除重力加速度吗?
- INS机械编排中旋转效应等补偿项,对于低端IMU是否需要补偿?
- 组合导航中GNSS信号丢失期间进行纯惯导解算,这时IMU误差项可以补偿吗?
- IMU数据,如何从速率形式转到增量形式?
- IMU零偏和比例因子建模时相关时间如何给定?
- GNSS/INS组合导航中是否需要考虑惯性系和车体系的转换?
- 初始化拓展
- 观测信息拓展
- 状态信息拓展
七、捷联惯导更新:insPropagation()
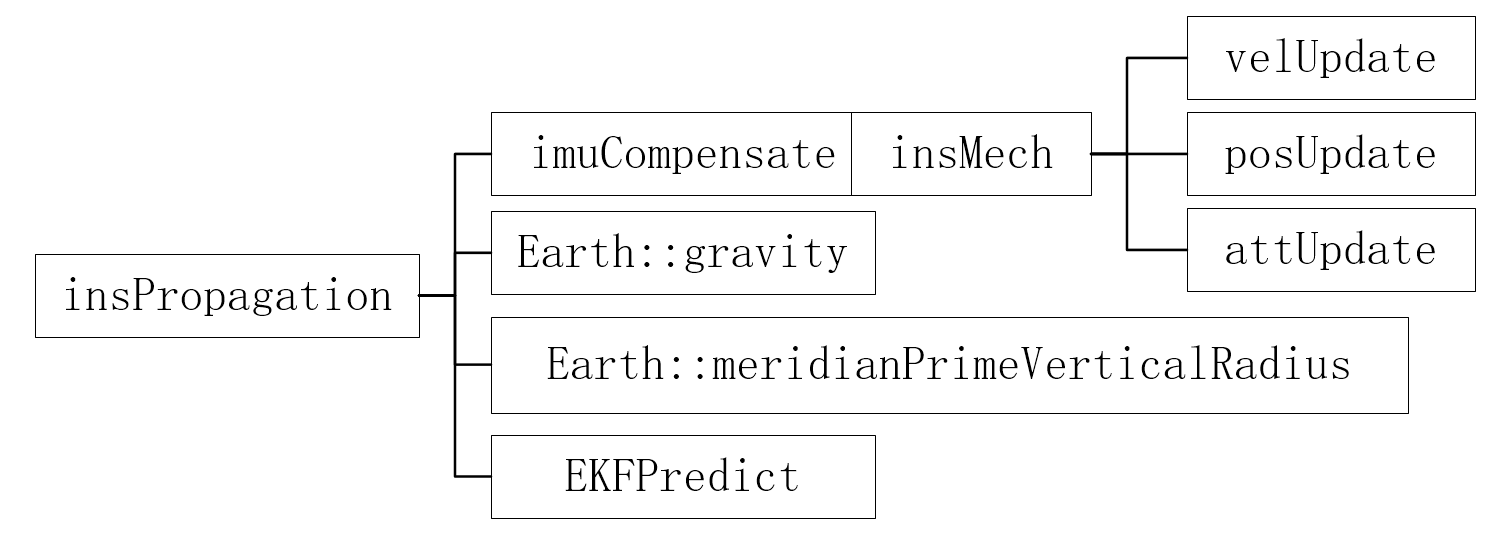
1、insPropagation():捷联惯导递推
根据两帧的 IMU 量测,将系统状态和误差状态从前一个 IMU 时间递推到后一个 IMU 时间;主要有三个步骤:IMU 误差补偿、状态更新(机械编排)、噪声传播。
先调用 imuCompensate(),补偿当前时刻 IMU 量测,就是减去零偏、除以加上单位阵后的比例:
imuCompensate(imucur);
调用 insMech() 依次进行速度更新、位置更新、姿态更新:
INSMech::insMech(pvapre_, pvacur_, imupre, imucur);
之后一大段是误差传播,后面详细介绍。
2、imuCompensate():IMU数据误差补偿
减去零偏、除以加上单位阵后的比例:
diag
(
I
+
s
‾
g
)
−
1
(
ω
~
i
b
b
−
b
‾
g
)
=
ω
^
i
b
b
diag
(
I
+
s
‾
a
)
−
1
(
f
~
i
b
b
−
b
‾
a
)
=
f
^
i
b
b
\begin{array}{l}\operatorname{diag}\left(\boldsymbol{I}+\overline{\boldsymbol{s}}_{g}\right)^{-1}\left(\tilde{\boldsymbol{\omega}}_{i b}^{b}-\overline{\boldsymbol{b}}_{g}\right)=\hat{\boldsymbol{\omega}}_{i b}^{b} \\ \operatorname{diag}\left(\boldsymbol{I}+\overline{\boldsymbol{s}}_{a}\right)^{-1}\left(\tilde{\boldsymbol{f}}_{i b}^{b}-\overline{\boldsymbol{b}}_{a}\right)=\hat{\boldsymbol{f}}_{i b}^{b}\end{array}
diag(I+sg)−1(ω~ibb−bg)=ω^ibbdiag(I+sa)−1(f~ibb−ba)=f^ibb
void GIEngine::imuCompensate(IMU &imu) {
// 补偿IMU零偏
// compensate the imu bias
imu.dtheta -= imuerror_.gyrbias * imu.dt;
imu.dvel -= imuerror_.accbias * imu.dt;
// 补偿IMU比例因子
// compensate the imu scale
Eigen::Vector3d gyrscale, accscale;
gyrscale = Eigen::Vector3d::Ones() + imuerror_.gyrscale;
accscale = Eigen::Vector3d::Ones() + imuerror_.accscale;
imu.dtheta = imu.dtheta.cwiseProduct(gyrscale.cwiseInverse());
imu.dvel = imu.dvel.cwiseProduct(accscale.cwiseInverse());
}
3、insMech():IMU 状态更新(机械编排)

依次进行速度更新、位置更新、姿态更新,不可调换顺序。

void INSMech::insMech(const PVA &pvapre, PVA &pvacur, const IMU &imupre, const IMU &imucur) {
// perform velocity update, position updata and attitude update in sequence, irreversible order
// 依次进行速度更新、位置更新、姿态更新, 不可调换顺序
velUpdate(pvapre, pvacur, imupre, imucur);
posUpdate(pvapre, pvacur, imupre, imucur);
attUpdate(pvapre, pvacur, imupre, imucur);
}
- PVA 更新都是先计算中间时刻的速度位置,进而计算中间时刻地球相关参数,再由此计算当前时刻 PVA;我觉得相比直接用上一时刻地球相关参数计算当前 PVA,精度提升不大。
- 位置更新中:先计算 n 系到 e 系旋转四元数,再调用
blh()计算经纬度。- 我觉得因为 PVA 写成三个函数,部分计算过程有重复,写在同一个函数实现能更简洁一些。
4、velUpdate():速度更新
1. 算法
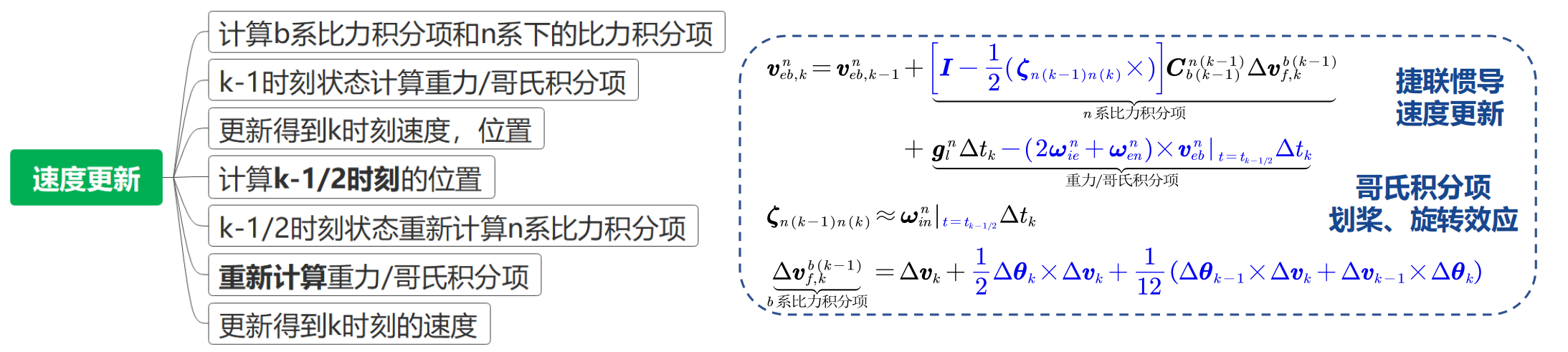
速度更新主要有两部分要算:
- 比力积分项:其中需要补偿划桨效应,是快变量,需要仔细积分。
- 有害加速度积分项:包括重力、哥氏加速度、向心力,是慢变量,直接梯形积分,用中间时刻来算。
然后,当前时刻的速度 = 上一时刻速度 + 比力积分项 + 有害加速度积分项:
v
e
b
,
k
n
=
v
e
b
,
k
−
1
n
+
[
I
−
1
2
(
ζ
n
(
k
−
1
)
n
(
k
)
×
)
]
C
b
(
k
−
1
)
n
(
k
−
1
)
Δ
v
f
,
k
b
(
k
−
1
)
⏟
n
系比力积分项
+
g
l
n
Δ
t
k
−
(
2
ω
i
n
+
ω
e
n
n
)
×
v
e
b
n
∣
t
=
t
k
−
1
/
2
Δ
t
k
⏟
重力/哥氏积分项
\begin{aligned} \boldsymbol{v}_{e b, k}^{n}=\boldsymbol{v}_{e b, k-1}^{n} & +\underbrace{\left[\boldsymbol{I}-\frac{1}{2}\left(\boldsymbol{\zeta}_{n(k-1) n(k)} \times\right)\right] \boldsymbol{C}_{b(k-1)}^{n(k-1)} \Delta \boldsymbol{v}_{f, k}^{b(k-1)}}_{n \text { 系比力积分项 }} \\ & +\underbrace{\boldsymbol{g}_{l}^{n} \Delta t_{k}-\left(2 \boldsymbol{\omega}_{i}^{n}+\boldsymbol{\omega}_{e n}^{n}\right) \times\left.\boldsymbol{v}_{e b}^{n}\right|_{t=t_{k-1 / 2}} \Delta t_{k}}_{\text {重力/哥氏积分项 }}\end{aligned}
veb,kn=veb,k−1n+n 系比力积分项
[I−21(ζn(k−1)n(k)×)]Cb(k−1)n(k−1)Δvf,kb(k−1)+重力/哥氏积分项
glnΔtk−(2ωin+ωenn)×vebn∣t=tk−1/2Δtk
2. 代码实现
先定义解算过程中涉及的中间变量:
Eigen::Vector3d d_vfb, d_vfn, d_vgn, gl, midvel, midpos;
Eigen::Vector3d temp1, temp2, temp3;
Eigen::Matrix3d cnn, I33 = Eigen::Matrix3d::Identity();
Eigen::Quaterniond qne, qee, qnn, qbb, q1, q2;
调用 meridianPrimeVerticalRadius(),根据上一时刻位置计算子午圈、卯酉圈半径:
R
M
=
R
e
(
1
−
e
2
)
(
1
−
e
2
sin
2
L
)
3
/
2
、
R
N
=
R
e
1
−
e
2
sin
2
L
R_{M}=\frac{R_{e}\left(1-e^{2}\right)}{\left(1-e^{2} \sin ^{2} L\right)^{3 / 2}}、R_{N}=\frac{R_{e}}{\sqrt{1-e^{2} \sin ^{2} L}}
RM=(1−e2sin2L)3/2Re(1−e2)、RN=1−e2sin2LRe
Eigen::Vector2d rmrn = Earth::meridianPrimeVerticalRadius(pvapre.pos(0));
计算地球自转引起的导航系旋转 wie_n:
ω
i
e
n
=
[
ω
e
cos
φ
0
−
ω
e
sin
φ
]
T
\boldsymbol{\omega}_{i e}^{n}=\left[\begin{array}{lll}\omega_{e} \cos \varphi & 0 & -\omega_{e} \sin \varphi\end{array}\right]^{\mathrm{T}}
ωien=[ωecosφ0−ωesinφ]T
wie_n << WGS84_WIE * cos(pvapre.pos[0]), 0, -WGS84_WIE * sin(pvapre.pos[0]);
计算载体在地球表面移动因地球曲率引起的导航系旋转 wen_n:
ω
e
n
n
=
[
v
E
/
(
R
N
+
h
)
−
v
N
/
(
R
M
+
h
)
−
v
E
tan
φ
/
(
R
N
+
h
)
]
\boldsymbol{\omega}_{e n}^{n}=\left[\begin{array}{c}v_{E} /\left(R_{N}+h\right) \\ -v_{N} /\left(R_{M}+h\right) \\ -v_{E} \tan \varphi /\left(R_{N}+h\right)\end{array}\right]
ωenn=
vE/(RN+h)−vN/(RM+h)−vEtanφ/(RN+h)
wen_n << pvapre.vel[1] / (rmrn[1] + pvapre.pos[2]), -pvapre.vel[0] / (rmrn[0] + pvapre.pos[2]),
-pvapre.vel[1] * tan(pvapre.pos[0]) / (rmrn[1] + pvapre.pos[2]);
调用 gravity(),根据上一时刻位置计算**重力 ** gravity:
g
L
=
9.7803267715
×
(
1
+
0.0052790414
×
sin
2
L
−
0.0000232718
×
sin
2
2
L
)
+
h
×
(
0.0000000043977311
×
sin
2
L
−
0.0000030876910891
)
+
0.0000000000007211
×
sin
4
2
L
g_{L}=9.7803267715 \times\left(1+0.0052790414 \times \sin ^{2} L-0.0000232718 \times \sin ^{2} 2 L\right) \\ +h\times(0.0000000043977311\times\sin ^{2} L-0.0000030876910891)+0.0000000000007211\times\sin ^{4} 2 L
gL=9.7803267715×(1+0.0052790414×sin2L−0.0000232718×sin22L)+h×(0.0000000043977311×sin2L−0.0000030876910891)+0.0000000000007211×sin42L
double gravity = Earth::gravity(pvapre.pos);
计算 b 系比力积分项 d_vfb,单子样 + 前一周期补偿划桨效应:
Δ
v
f
,
k
−
1
)
b
(
k
−
1
)
⏟
b
系比力积分项
=
Δ
v
k
+
1
2
Δ
θ
k
×
Δ
v
k
+
1
12
(
Δ
θ
k
−
1
×
Δ
v
k
+
Δ
v
k
−
1
×
Δ
θ
k
)
\underbrace{\Delta \boldsymbol{v}_{f, k-1)}^{b(k-1)}}_{b \text { 系比力积分项 }}=\Delta \boldsymbol{v}_{k}+\frac{1}{2} \Delta \boldsymbol{\theta}_{k} \times \Delta \boldsymbol{v}_{k}+\frac{1}{12}\left(\Delta \boldsymbol{\theta}_{k-1} \times \Delta \boldsymbol{v}_{k}+\Delta \boldsymbol{v}_{k-1} \times \Delta \boldsymbol{\theta}_{k}\right)
b 系比力积分项
Δvf,k−1)b(k−1)=Δvk+21Δθk×Δvk+121(Δθk−1×Δvk+Δvk−1×Δθk)
// 旋转效应和双子样划桨效应
// rotational and sculling motion
temp1 = imucur.dtheta.cross(imucur.dvel) / 2;
temp2 = imupre.dtheta.cross(imucur.dvel) / 12;
temp3 = imupre.dvel.cross(imucur.dtheta) / 12;
// b系比力积分项
// velocity increment due to the specific force
d_vfb = imucur.dvel + temp1 + temp2 + temp3;
比力积分项投影到 n 系,三行代码分别对应的公式为:
ω
i
n
n
=
ω
i
e
n
+
ω
e
n
n
{\omega}_{i n}^{n}={\omega}_{i e}^{n}+{\omega}_{e n}^{n}
ωinn=ωien+ωenn
ζ n ( k − 1 ) n ( k ) ≈ ω i n n ∣ t = t k − 1 / 2 Δ t k \left.\boldsymbol{\zeta}_{n(k-1) n(k)} \approx \boldsymbol{\omega}_{i n}^{n}\right|_{t=t_{k-1 / 2}} \Delta t_{k} ζn(k−1)n(k)≈ωinn t=tk−1/2Δtk
[ I − 1 2 ( ζ n ( k − 1 ) n ( k ) × ) ] C b ( k − 1 ) n ( k − 1 ) Δ v f , k b ( k − 1 ) ⏟ n 系比力积分项 \underbrace{\left[\boldsymbol{I}-\frac{1}{2}\left(\boldsymbol{\zeta}_{n(k-1) n(k)} \times\right)\right] \boldsymbol{C}_{b(k-1)}^{n(k-1)} \Delta \boldsymbol{v}_{f, k}^{b(k-1)}}_{n \text { 系比力积分项 }} n 系比力积分项 [I−21(ζn(k−1)n(k)×)]Cb(k−1)n(k−1)Δvf,kb(k−1)
// 比力积分项投影到n系
// velocity increment dut to the specfic force projected to the n-frame
temp1 = (wie_n + wen_n) * imucur.dt / 2;
cnn = I33 - Rotation::skewSymmetric(temp1);
d_vfn = cnn * pvapre.att.cbn * d_vfb;
计算重力/哥式积分项:
g
l
n
Δ
t
k
−
(
2
ω
i
n
+
ω
e
n
n
)
×
v
e
b
n
∣
t
=
t
k
−
1
/
2
Δ
t
k
⏟
重力/哥氏积分项
\underbrace{\boldsymbol{g}_{l}^{n} \Delta t_{k}-\left(2 \boldsymbol{\omega}_{i}^{n}+\boldsymbol{\omega}_{e n}^{n}\right) \times\left.\boldsymbol{v}_{e b}^{n}\right|_{t=t_{k-1 / 2}} \Delta t_{k}}_{\text {重力/哥氏积分项 }}
重力/哥氏积分项
glnΔtk−(2ωin+ωenn)×vebn∣t=tk−1/2Δtk
// 计算重力/哥式积分项
// velocity increment due to the gravity and Coriolis force
gl << 0, 0, gravity;
d_vgn = (gl - (2 * wie_n + wen_n).cross(pvapre.vel)) * imucur.dt;
上一时刻速度加上一半比力积分项和比力积分项,得到中间时刻速度:
// 得到中间时刻速度
// velocity at k-1/2
midvel = pvapre.vel + (d_vfn + d_vgn) / 2;
外推得到中间时刻位置:
- 计算两时刻n系旋转四元数
qnn - 根据地球自转角速率,计算两时刻e系旋转四元数
qee - 调用
qne根据先前时刻位置,计算先前时刻n系到e系旋转四元数qne - 当前时刻 n 系到 e 系旋转四元数
qne= 两时刻e系旋转四元数 * 先前n系到e系旋转四元数 * 两时刻 n 系旋转四元数 - 中间时刻高程 = 先前高程 - 高程方向速度 * 一半采样周期(因为北东地,计算出的速度时地向的,所以减)
- 调用
blh()根据 n系到e系旋转四元数计算经纬度
// 外推得到中间时刻位置
// position extrapolation to k-1/2
qnn = Rotation::rotvec2quaternion(temp1);
temp2 << 0, 0, -WGS84_WIE * imucur.dt / 2;
qee = Rotation::rotvec2quaternion(temp2);
qne = Earth::qne(pvapre.pos);
qne = qee * qne * qnn;
midpos[2] = pvapre.pos[2] - midvel[2] * imucur.dt / 2;
midpos = Earth::blh(qne, midpos[2]);
基于用中间时刻的位置,重新做一遍之前的操作:
- 重新计算中间时刻的地理参数:
rmrn、wie_n、wen_n(重力没重算) - 重新计算 n 系下平均比力积分项:
d_vfn - 重新计算重力、哥式积分项:
d_vgn
// 重新计算中间时刻的 rmrn, wie_e, wen_n
// recompute rmrn, wie_n, and wen_n at k-1/2
rmrn = Earth::meridianPrimeVerticalRadius(midpos[0]);
wie_n << WGS84_WIE * cos(midpos[0]), 0, -WGS84_WIE * sin(midpos[0]);
wen_n << midvel[1] / (rmrn[1] + midpos[2]), -midvel[0] / (rmrn[0] + midpos[2]),
-midvel[1] * tan(midpos[0]) / (rmrn[1] + midpos[2]);
// 重新计算n系下平均比力积分项
// recompute d_vfn
temp3 = (wie_n + wen_n) * imucur.dt / 2;
cnn = I33 - Rotation::skewSymmetric(temp3);
d_vfn = cnn * pvapre.att.cbn * d_vfb;
// 重新计算重力、哥式积分项
// recompute d_vgn
gl << 0, 0, Earth::gravity(midpos);
d_vgn = (gl - (2 * wie_n + wen_n).cross(midvel)) * imucur.dt;
最后,用上一时刻的速度,加上n系下平均比力积分项、重力/哥式积分项,得到当前时刻速度:
v
e
b
,
k
n
=
v
e
b
,
k
−
1
n
+
[
I
−
1
2
(
ζ
n
(
k
−
1
)
n
(
k
)
×
)
]
C
b
(
k
−
1
)
n
(
k
−
1
)
Δ
v
f
,
k
b
(
k
−
1
)
⏟
n
系比力积分项
+
g
l
n
Δ
t
k
−
(
2
ω
i
n
+
ω
e
n
n
)
×
v
e
b
n
∣
t
=
t
k
−
1
/
2
Δ
t
k
⏟
重力/哥氏积分项
\begin{aligned} \boldsymbol{v}_{e b, k}^{n}=\boldsymbol{v}_{e b, k-1}^{n} & +\underbrace{\left[\boldsymbol{I}-\frac{1}{2}\left(\boldsymbol{\zeta}_{n(k-1) n(k)} \times\right)\right] \boldsymbol{C}_{b(k-1)}^{n(k-1)} \Delta \boldsymbol{v}_{f, k}^{b(k-1)}}_{n \text { 系比力积分项 }} \\ & +\underbrace{\boldsymbol{g}_{l}^{n} \Delta t_{k}-\left(2 \boldsymbol{\omega}_{i}^{n}+\boldsymbol{\omega}_{e n}^{n}\right) \times\left.\boldsymbol{v}_{e b}^{n}\right|_{t=t_{k-1 / 2}} \Delta t_{k}}_{\text {重力/哥氏积分项 }}\end{aligned}
veb,kn=veb,k−1n+n 系比力积分项
[I−21(ζn(k−1)n(k)×)]Cb(k−1)n(k−1)Δvf,kb(k−1)+重力/哥氏积分项
glnΔtk−(2ωin+ωenn)×vebn∣t=tk−1/2Δtk
pvacur.vel = pvapre.vel + d_vfn + d_vgn;
5、posUpdate():位置更新
1. 算法

先计算当前时刻 n 系到 e 系旋转四元数 qne,再以此算经纬度。其中,当前时刻 qne 的计算分为三部分:
-
先前时刻 qne:通过上一时刻经纬度计算。
-
两时刻 n 系变化 qnn:由地球自转角速度、牵连角速度两部分引起。
-
两时刻 e 系变化 qee:地球自转角速度乘以时间差。
然后,当前时刻n系到e系旋转四元数 = 两时刻e系旋转四元数 * 先前n系到e系旋转四元数 * 两时刻n系旋转四元数。
2. 代码实现
先定义解算过程中涉及的中间变量:
Eigen::Vector3d temp1, temp2, midvel, midpos;
Eigen::Quaterniond qne, qee, qnn;
重新计算中间时刻的速度 midvel 和位置 midpos:
- 中间时刻速度:取两时刻的平均。
- 中间时刻位置:上一时刻位置 + 平均速度 * 一半采样间隔。
// 重新计算中间时刻的速度和位置
// recompute velocity and position at k-1/2
midvel = (pvacur.vel + pvapre.vel) / 2;
midpos = pvapre.pos + Earth::DRi(pvapre.pos) * midvel * imucur.dt / 2;
根据中间时刻位置, 重新计算中间时刻地理参数(除了重力):
// 重新计算中间时刻地理参数
// recompute rmrn, wie_n, wen_n at k-1/2
Eigen::Vector2d rmrn;
Eigen::Vector3d wie_n, wen_n;
rmrn = Earth::meridianPrimeVerticalRadius(midpos[0]);
wie_n << WGS84_WIE * cos(midpos[0]), 0, -WGS84_WIE * sin(midpos[0]);
wen_n << midvel[1] / (rmrn[1] + midpos[2]), -midvel[0] / (rmrn[0] + midpos[2]),
-midvel[1] * tan(midpos[0]) / (rmrn[1] + midpos[2]);
重新计算 k 时刻到 k-1 时刻 n 系旋转矢量:
ω
i
n
n
=
ω
i
e
n
+
ω
e
n
n
{\omega}_{i n}^{n}={\omega}_{i e}^{n}+{\omega}_{e n}^{n}
ωinn=ωien+ωenn
ζ n ( k − 1 ) n ( k ) ≈ ω i n n ∣ t = t k − 1 / 2 Δ t k \left.\boldsymbol{\zeta}_{n(k-1) n(k)} \approx \boldsymbol{\omega}_{i n}^{n}\right|_{t=t_{k-1 / 2}} \Delta t_{k} ζn(k−1)n(k)≈ωinn t=tk−1/2Δtk
// 重新计算 k 时刻到 k-1 时刻 n系旋转矢量
// recompute n-frame rotation vector (n(k) with respect to n(k-1)-frame)
temp1 = (wie_n + wen_n) * imucur.dt;
qnn = Rotation::rotvec2quaternion(temp1);
e 系转动等效旋转矢量 (k-1时刻k时刻,所以取负号),直接就是地球自转角速率乘以时间差:
// e系转动等效旋转矢量 (k-1时刻k时刻,所以取负号)
// e-frame rotation vector (e(k-1) with respect to e(k)-frame)
temp2 << 0, 0, -WGS84_WIE * imucur.dt;
qee = Rotation::rotvec2quaternion(temp2);
由先前时刻位置,调用 qne(),得到先前n系到e系旋转四元数:
qne = Earth::qne(pvapre.pos);
当前时刻n系到e系旋转四元数 = 两时刻e系旋转四元数 * 先前n系到e系旋转四元数 * 两时刻n系旋转四元数:
qne = qee * qne * qnn;
当前时刻高程 = 先前高程 - 高程方向速度 * 采样间隔(因为北东地,计算出的速度时地向的,所以减):
pvacur.pos[2] = pvapre.pos[2] - midvel[2] * imucur.dt;
调用 blh() 根据 n 系到 e 系旋转四元数计算经纬度:
pvacur.pos = Earth::blh(qne, pvacur.pos[2]);
6、attUpdate():姿态更新
1. 算法

姿态更新主要也算两部分:
- 两时刻 n 系的变化:由地球自转角速度、牵连角速度两部分引起。
- 两时刻 b 系的变化:通过 IMU 角增量量测值计算,需补偿圆锥运动。
然后,两时刻 n 系的旋转四元数 * 上一时刻姿态四元数 * 两时刻 b 系旋转四元数得到当前姿态:
q
b
k
n
k
=
q
n
k
−
1
n
k
q
b
k
−
1
n
k
−
1
q
b
k
b
k
−
1
\boldsymbol{q}_{b_{k}}^{n_{k}}=\boldsymbol{q}_{n_{k-1}}^{n_{k}} \boldsymbol{q}_{b_{k-1}}^{n_{k-1}} \boldsymbol{q}_{b_{k}}^{b_{k-1}}
qbknk=qnk−1nkqbk−1nk−1qbkbk−1
2. 代码实现
先定义解算过程中涉及的中间变量:
Eigen::Quaterniond qne_pre, qne_cur, qne_mid, qnn, qbb;
Eigen::Vector3d temp1, midpos, midvel;
重新计算中间时刻的速度和位置,中间速度是两时刻平均、中间位置相对于是作了一次位置更新:
- 根据两时刻速度,计算平均速度
midvel - 根据上一时刻位置计算n系到e系转换四元数
qne_pre - 根据当前时刻位置计算n系到e系转换四元数
qne_cur - 根据两时刻转换四元数,计算n系到e系平均转换四元数
qne_mid(注意得通过等效旋转矢量,并非直接插值) - 计算当前中间时刻位置
midpos
// 重新计算中间时刻的速度和位置
// recompute velocity and position at k-1/2
midvel = (pvapre.vel + pvacur.vel) / 2;
qne_pre = Earth::qne(pvapre.pos);
qne_cur = Earth::qne(pvacur.pos);
temp1 = Rotation::quaternion2vector(qne_cur.inverse() * qne_pre);
qne_mid = qne_pre * Rotation::rotvec2quaternion(temp1 / 2).inverse();
midpos[2] = (pvacur.pos[2] + pvapre.pos[2]) / 2;
midpos = Earth::blh(qne_mid, midpos[2]);
重新计算中间时刻地理参数:
// 重新计算中间时刻地理参数
// recompute rmrn, wie_n, wen_n at k-1/2
Eigen::Vector2d rmrn;
Eigen::Vector3d wie_n, wen_n;
rmrn = Earth::meridianPrimeVerticalRadius(midpos[0]);
wie_n << WGS84_WIE * cos(midpos[0]), 0, -WGS84_WIE * sin(midpos[0]);
wen_n << midvel[1] / (rmrn[1] + midpos[2]), -midvel[0] / (rmrn[0] + midpos[2]),
-midvel[1] * tan(midpos[0]) / (rmrn[1] + midpos[2]);
计算 n 系的旋转四元数 k-1 时刻到 k 时刻系旋转:
ω
i
n
n
=
ω
i
e
n
+
ω
e
n
n
{\omega}_{i n}^{n}={\omega}_{i e}^{n}+{\omega}_{e n}^{n}
ωinn=ωien+ωenn
ζ n ( k − 1 ) n ( k ) ≈ ω i n n ∣ t = t k − 1 / 2 Δ t k \left.\boldsymbol{\zeta}_{n(k-1) n(k)} \approx \boldsymbol{\omega}_{i n}^{n}\right|_{t=t_{k-1 / 2}} \Delta t_{k} ζn(k−1)n(k)≈ωinn t=tk−1/2Δtk
// 重新计算 k时刻到k-1时刻 n系旋转矢量
// recompute n-frame rotation vector (n(k) with respect to n(k-1)-frame)
temp1 = (wie_n + wen_n) * imucur.dt;
qnn = Rotation::rotvec2quaternion(temp1);
计算 b 系旋转四元数补偿二阶圆锥误差:
q
b
k
b
k
−
1
←
ϕ
k
=
Δ
θ
k
+
1
12
Δ
θ
k
−
1
×
Δ
θ
k
\boldsymbol{q}_{b_{k}}^{b_{k-1}} \leftarrow \boldsymbol{\phi}_{k}=\Delta \boldsymbol{\theta}_{k}+\frac{1}{12} \Delta \boldsymbol{\theta}_{k-1} \times \Delta \boldsymbol{\theta}_{k}
qbkbk−1←ϕk=Δθk+121Δθk−1×Δθk
// 计算b系旋转四元数 补偿二阶圆锥误差
// b-frame rotation vector (b(k) with respect to b(k-1)-frame)
// compensate the second-order coning correction term.
temp1 = imucur.dtheta + imupre.dtheta.cross(imucur.dtheta) / 12;
qbb = Rotation::rotvec2quaternion(temp1);
两时刻 n 系的旋转四元数 * 上一时刻姿态四元数 * 两时刻 b 系旋转四元数得到当前姿态:
q
b
k
n
k
=
q
n
k
−
1
n
k
q
b
k
−
1
n
k
−
1
q
b
k
b
k
−
1
\boldsymbol{q}_{b_{k}}^{n_{k}}=\boldsymbol{q}_{n_{k-1}}^{n_{k}} \boldsymbol{q}_{b_{k-1}}^{n_{k-1}} \boldsymbol{q}_{b_{k}}^{b_{k-1}}
qbknk=qnk−1nkqbk−1nk−1qbkbk−1
// 姿态更新完成
// attitude update finish
pvacur.att.qbn = qnn * pvapre.att.qbn * qbb;
pvacur.att.cbn = Rotation::quaternion2matrix(pvacur.att.qbn);
pvacur.att.euler = Rotation::matrix2euler(pvacur.att.cbn);
7、误差传播
就是协方差的更新:
-
先构造连续时间的 F F F 矩阵,离散化得到状态转移矩阵 Φ k / k − 1 = I + F k − 1 Δ t k \boldsymbol{\Phi}_{k / k-1}=\boldsymbol{I}+\boldsymbol{F}_{k-1} \Delta t_{k} Φk/k−1=I+Fk−1Δtk ,
-
gi_engine初始化的用角速度随机游走 arw、加速度随机游走 vrw,角速度零偏白噪声、加速度零偏白噪声、角速度比例、加速度零偏比例构造了恒定的 18 18 18 维噪声阵Qc_。然后每次惯导更新的时候计算一个 21 × 18 21 \times 18 21×18 维 噪声驱动阵G,计算得到噪声阵。
Q k = ( Φ k / k − 1 G k − 1 q k − 1 G k − 1 T Φ k / k − 1 T + G k q k G k T ) Δ t k / 2 \boldsymbol{Q}_{k}=\left(\begin{array}{c}\boldsymbol{\Phi}_{k / k-1} \boldsymbol{G}_{k-1} \boldsymbol{q}_{k-1} \boldsymbol{G}_{k-1}^{T} \boldsymbol{\Phi}_{k / k-1}^{T} \\ +\boldsymbol{G}_{k} \boldsymbol{q}_{k} \boldsymbol{G}_{k}^{T}\end{array}\right) \Delta t_{k} / 2 Qk=(Φk/k−1Gk−1qk−1Gk−1TΦk/k−1T+GkqkGkT)Δtk/2 -
用状态转移矩阵和噪声阵卡尔曼滤波时间更新协方差阵
cov_和状态向量dx_,如果误差反馈状态向量是 0,无需更新。
x k / k − 1 = Φ k / k − 1 x k − 1 P k / k − 1 = Φ k / k − 1 P k − 1 Φ k / k − 1 T + Q k \begin{aligned} \boldsymbol{x}_{k / k-1} & =\boldsymbol{\Phi}_{k / k-1} \boldsymbol{x}_{k-1} \\ \boldsymbol{P}_{k / k-1} & =\boldsymbol{\Phi}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{\Phi}_{k / k-1}^{T}+\boldsymbol{Q}_{k}\end{aligned} xk/k−1Pk/k−1=Φk/k−1xk−1=Φk/k−1Pk−1Φk/k−1T+Qk
下面介绍具体公式和代码:
在 insPropagation() 函数中,IMU状态更新之后进行。
先要构建 F 矩阵:
F
=
[
F
r
r
I
3
×
3
0
0
0
0
0
F
v
r
F
v
v
[
(
C
b
n
f
b
)
×
]
0
C
b
n
0
C
b
n
diag
(
f
b
)
F
ϕ
r
F
ϕ
v
−
(
ω
i
n
n
×
)
−
C
b
n
0
−
C
b
n
diag
(
ω
i
b
b
)
0
0
0
0
−
1
T
g
b
I
3
×
3
0
0
0
0
0
0
0
−
1
T
a
b
I
3
×
3
0
0
0
0
0
0
0
−
1
T
g
s
I
3
×
3
0
0
0
0
0
0
0
−
1
T
a
s
I
3
×
3
]
\mathbf{F}=\left[\begin{array}{ccccccc}\mathbf{F}_{r r} & \mathbf{I}_{3 \times 3} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{F}_{v r} & \mathbf{F}_{v v} & {\left[\left(\mathbf{C}_{b}^{n} \boldsymbol{f}^{b}\right) \times\right]} & \mathbf{0} & \mathbf{C}_{b}^{n} & \mathbf{0} & \mathbf{C}_{b}^{n} \operatorname{diag}\left(\boldsymbol{f}^{b}\right) \\ \mathbf{F}_{\phi r} & \mathbf{F}_{\phi v} & -\left(\boldsymbol{\omega}_{i n}^{n} \times\right) & -\mathbf{C}_{b}^{n} & \mathbf{0} & -\mathbf{C}_{b}^{n} \operatorname{diag}\left(\boldsymbol{\omega}_{i b}^{b}\right) & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \frac{-1}{T_{g b}} \mathbf{I}_{3 \times 3} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \frac{-1}{T_{a b}} \mathbf{I}_{3 \times 3} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \frac{-1}{T_{g s}} \mathbf{I}_{3 \times 3} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \frac{-1}{T_{a s}} \mathbf{I}_{3 \times 3}\end{array}\right]
F=
FrrFvrFϕr0000I3×3FvvFϕv00000[(Cbnfb)×]−(ωinn×)000000−CbnTgb−1I3×30000Cbn00Tab−1I3×30000−Cbndiag(ωibb)00Tgs−1I3×300Cbndiag(fb)0000Tas−1I3×3
上面 F 矩阵每一块都是一个
3
×
3
3 \times 3
3×3 矩阵,分别表示位置、速度、姿态、陀螺仪零偏、加速度计零偏、陀螺仪比例、加速度计比力,共21维。可以很明显的看出左上角几乎是满的,因为位置、速度、姿态之间误差耦合很深;右下的器件误差很稀释,因为我们认为器件与器件之间的量测是相互独立的,处理在对角线上有元素之外,只在与器件相关的位置有元素(陀螺仪和姿态相关、加速度计和速度相关)。
定义了枚举值来索引左上角元素的下标:
enum StateID { P_ID = 0, V_ID = 3, PHI_ID = 6,
BG_ID = 9, BA_ID = 12, SG_ID = 15, SA_ID = 18 };
代码排的很整齐,遵循从左往右、从上往下的顺序计算:
// 位置误差
// position error
temp.setZero();
temp(0, 0) = -pvapre_.vel[2] / rmh;
temp(0, 2) = pvapre_.vel[0] / rmh;
temp(1, 0) = pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh;
temp(1, 1) = -(pvapre_.vel[2] + pvapre_.vel[0] * tan(pvapre_.pos[0])) / rnh;
temp(1, 2) = pvapre_.vel[1] / rnh;
F.block(P_ID, P_ID, 3, 3) = temp;
F.block(P_ID, V_ID, 3, 3) = Eigen::Matrix3d::Identity();
// 速度误差
// velocity error
temp.setZero();
temp(0, 0) = -2 * pvapre_.vel[1] * WGS84_WIE * cos(pvapre_.pos[0]) / rmh -
pow(pvapre_.vel[1], 2) / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(0, 2) = pvapre_.vel[0] * pvapre_.vel[2] / rmh / rmh - pow(pvapre_.vel[1], 2) * tan(pvapre_.pos[0]) / rnh / rnh;
temp(1, 0) = 2 * WGS84_WIE * (pvapre_.vel[0] * cos(pvapre_.pos[0]) - pvapre_.vel[2] * sin(pvapre_.pos[0])) / rmh +
pvapre_.vel[0] * pvapre_.vel[1] / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(1, 2) = (pvapre_.vel[1] * pvapre_.vel[2] + pvapre_.vel[0] * pvapre_.vel[1] * tan(pvapre_.pos[0])) / rnh / rnh;
temp(2, 0) = 2 * WGS84_WIE * pvapre_.vel[1] * sin(pvapre_.pos[0]) / rmh;
temp(2, 2) = -pow(pvapre_.vel[1], 2) / rnh / rnh - pow(pvapre_.vel[0], 2) / rmh / rmh +
2 * gravity / (sqrt(rmrn[0] * rmrn[1]) + pvapre_.pos[2]);
F.block(V_ID, P_ID, 3, 3) = temp;
temp.setZero();
temp(0, 0) = pvapre_.vel[2] / rmh;
temp(0, 1) = -2 * (WGS84_WIE * sin(pvapre_.pos[0]) + pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh);
temp(0, 2) = pvapre_.vel[0] / rmh;
temp(1, 0) = 2 * WGS84_WIE * sin(pvapre_.pos[0]) + pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh;
temp(1, 1) = (pvapre_.vel[2] + pvapre_.vel[0] * tan(pvapre_.pos[0])) / rnh;
temp(1, 2) = 2 * WGS84_WIE * cos(pvapre_.pos[0]) + pvapre_.vel[1] / rnh;
temp(2, 0) = -2 * pvapre_.vel[0] / rmh;
temp(2, 1) = -2 * (WGS84_WIE * cos(pvapre_.pos(0)) + pvapre_.vel[1] / rnh);
F.block(V_ID, V_ID, 3, 3) = temp;
F.block(V_ID, PHI_ID, 3, 3) = Rotation::skewSymmetric(pvapre_.att.cbn * accel);
F.block(V_ID, BA_ID, 3, 3) = pvapre_.att.cbn;
F.block(V_ID, SA_ID, 3, 3) = pvapre_.att.cbn * (accel.asDiagonal());
// 姿态误差
// attitude error
temp.setZero();
temp(0, 0) = -WGS84_WIE * sin(pvapre_.pos[0]) / rmh;
temp(0, 2) = pvapre_.vel[1] / rnh / rnh;
temp(1, 2) = -pvapre_.vel[0] / rmh / rmh;
temp(2, 0) = -WGS84_WIE * cos(pvapre_.pos[0]) / rmh - pvapre_.vel[1] / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(2, 2) = -pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh / rnh;
F.block(PHI_ID, P_ID, 3, 3) = temp;
temp.setZero();
temp(0, 1) = 1 / rnh;
temp(1, 0) = -1 / rmh;
temp(2, 1) = -tan(pvapre_.pos[0]) / rnh;
F.block(PHI_ID, V_ID, 3, 3) = temp;
F.block(PHI_ID, PHI_ID, 3, 3) = -Rotation::skewSymmetric(wie_n + wen_n);
F.block(PHI_ID, BG_ID, 3, 3) = -pvapre_.att.cbn;
F.block(PHI_ID, SG_ID, 3, 3) = -pvapre_.att.cbn * (omega.asDiagonal());
// IMU零偏误差和比例因子误差,建模成一阶高斯-马尔科夫过程
// imu bias error and scale error, modeled as the first-order Gauss-Markov process
F.block(BG_ID, BG_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(BA_ID, BA_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(SG_ID, SG_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(SA_ID, SA_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
其中:
F
r
r
=
[
−
v
D
R
M
+
h
0
v
N
R
M
+
h
v
E
tan
φ
R
N
+
h
−
v
D
+
v
N
tan
φ
R
N
+
h
v
E
R
N
+
h
0
0
0
]
\mathbf{F}_{r r}=\left[\begin{array}{ccc}-\frac{v_{D}}{R_{M}+h} & 0 & \frac{v_{N}}{R_{M}+h} \\ \frac{v_{E} \tan \varphi}{R_{N}+h} & -\frac{v_{D}+v_{N} \tan \varphi}{R_{N}+h} & \frac{v_{E}}{R_{N}+h} \\ 0 & 0 & 0\end{array}\right]
Frr=
−RM+hvDRN+hvEtanφ00−RN+hvD+vNtanφ0RM+hvNRN+hvE0
temp.setZero();
temp(0, 0) = -pvapre_.vel[2] / rmh;
temp(0, 2) = pvapre_.vel[0] / rmh;
temp(1, 0) = pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh;
temp(1, 1) = -(pvapre_.vel[2] + pvapre_.vel[0] * tan(pvapre_.pos[0])) / rnh;
temp(1, 2) = pvapre_.vel[1] / rnh;
F.block(P_ID, P_ID, 3, 3) = temp;
F v r = [ − 2 v E ω e cos φ R M + h − v E 2 sec 2 φ ( R M + h ) ( R N + h ) 0 v N v D ( R M + h ) 2 − v E 2 tan φ ( R N + h ) 2 2 ω e ( v N cos φ − v D sin φ ) R M + h + v N v E sec 2 φ ( R M + h ) ( R N + h ) 0 v E v D + v N v E tan φ ( R N + h ) 2 2 ω e v E sin φ R M + h 0 − v E 2 ( R N + h ) 2 − v N 2 ( R M + h ) 2 + 2 g p R M R N + h ] \mathbf{F}_{v r}=\left[\begin{array}{ccc}\frac{-2 v_{E} \omega_{e} \cos \varphi}{R_{M}+h}-\frac{v_{E}^{2} \sec ^{2} \varphi}{\left(R_{M}+h\right)\left(R_{N}+h\right)} & 0 & \frac{v_{N} v_{D}}{\left(R_{M}+h\right)^{2}}-\frac{v_{E}^{2} \tan \varphi}{\left(R_{N}+h\right)^{2}} \\ \frac{2 \omega_{e}\left(v_{N} \cos \varphi-v_{D} \sin \varphi\right)}{R_{M}+h}+\frac{v_{N} v_{E} \sec ^{2} \varphi}{\left(R_{M}+h\right)\left(R_{N}+h\right)} & 0 & \frac{v_{E} v_{D}+v_{N} v_{E} \tan \varphi}{\left(R_{N}+h\right)^{2}} \\ \frac{2 \omega_{e} v_{E} \sin \varphi}{R_{M}+h} & 0 & -\frac{v_{E}^{2}}{\left(R_{N}+h\right)^{2}}-\frac{v_{N}^{2}}{\left(R_{M}+h\right)^{2}}+\frac{2 g_{p}}{\sqrt{R_{M} R_{N}+h}}\end{array}\right] Fvr= RM+h−2vEωecosφ−(RM+h)(RN+h)vE2sec2φRM+h2ωe(vNcosφ−vDsinφ)+(RM+h)(RN+h)vNvEsec2φRM+h2ωevEsinφ000(RM+h)2vNvD−(RN+h)2vE2tanφ(RN+h)2vEvD+vNvEtanφ−(RN+h)2vE2−(RM+h)2vN2+RMRN+h2gp
temp.setZero();
temp(0, 0) = -2 * pvapre_.vel[1] * WGS84_WIE * cos(pvapre_.pos[0]) / rmh -
pow(pvapre_.vel[1], 2) / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(0, 2) = pvapre_.vel[0] * pvapre_.vel[2] / rmh / rmh - pow(pvapre_.vel[1], 2) * tan(pvapre_.pos[0]) / rnh / rnh;
temp(1, 0) = 2 * WGS84_WIE * (pvapre_.vel[0] * cos(pvapre_.pos[0]) - pvapre_.vel[2] * sin(pvapre_.pos[0])) / rmh +
pvapre_.vel[0] * pvapre_.vel[1] / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(1, 2) = (pvapre_.vel[1] * pvapre_.vel[2] + pvapre_.vel[0] * pvapre_.vel[1] * tan(pvapre_.pos[0])) / rnh / rnh;
temp(2, 0) = 2 * WGS84_WIE * pvapre_.vel[1] * sin(pvapre_.pos[0]) / rmh;
temp(2, 2) = -pow(pvapre_.vel[1], 2) / rnh / rnh - pow(pvapre_.vel[0], 2) / rmh / rmh +
2 * gravity / (sqrt(rmrn[0] * rmrn[1]) + pvapre_.pos[2]);
F.block(V_ID, P_ID, 3, 3) = temp;
F v v = [ v D R M + h − 2 ( ω e sin φ + v E tan φ R N + h ) v N R M + h 2 ω e sin φ + v E tan φ R N + h v D + v N tan φ R N + h 2 ω e cos φ + v E R N + h − 2 v N R M + h − 2 ( ω e cos φ + v E R N + h ) 0 ] \mathbf{F}_{v v}=\left[\begin{array}{ccc}\frac{v_{D}}{R_{M}+h} & -2\left(\omega_{e} \sin \varphi+\frac{v_{E} \tan \varphi}{R_{N}+h}\right) & \frac{v_{N}}{R_{M}+h} \\ 2 \omega_{e} \sin \varphi+\frac{v_{E} \tan \varphi}{R_{N}+h} & \frac{v_{D}+v_{N} \tan \varphi}{R_{N}+h} & 2 \omega_{e} \cos \varphi+\frac{v_{E}}{R_{N}+h} \\ -\frac{2 v_{N}}{R_{M}+h} & -2\left(\omega_{e} \cos \varphi+\frac{v_{E}}{R_{N}+h}\right) & 0\end{array}\right] Fvv= RM+hvD2ωesinφ+RN+hvEtanφ−RM+h2vN−2(ωesinφ+RN+hvEtanφ)RN+hvD+vNtanφ−2(ωecosφ+RN+hvE)RM+hvN2ωecosφ+RN+hvE0
temp.setZero();
temp(0, 0) = pvapre_.vel[2] / rmh;
temp(0, 1) = -2 * (WGS84_WIE * sin(pvapre_.pos[0]) + pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh);
temp(0, 2) = pvapre_.vel[0] / rmh;
temp(1, 0) = 2 * WGS84_WIE * sin(pvapre_.pos[0]) + pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh;
temp(1, 1) = (pvapre_.vel[2] + pvapre_.vel[0] * tan(pvapre_.pos[0])) / rnh;
temp(1, 2) = 2 * WGS84_WIE * cos(pvapre_.pos[0]) + pvapre_.vel[1] / rnh;
temp(2, 0) = -2 * pvapre_.vel[0] / rmh;
temp(2, 1) = -2 * (WGS84_WIE * cos(pvapre_.pos(0)) + pvapre_.vel[1] / rnh);
F.block(V_ID, V_ID, 3, 3) = temp;
F ϕ r = [ − ω e sin φ R M + h 0 v E ( R N + h ) 2 0 0 − v N ( R M + h ) 2 − ω e cos φ R M + h − v E sec 2 φ ( R M + h ) ( R N + h ) 0 − v E tan φ ( R N + h ) 2 ] \mathbf{F}_{\phi r}=\left[\begin{array}{ccc}-\frac{\omega_{e} \sin \varphi}{R_{M}+h} & 0 & \frac{v_{E}}{\left(R_{N}+h\right)^{2}} \\ 0 & 0 & -\frac{v_{N}}{\left(R_{M}+h\right)^{2}} \\ -\frac{\omega_{e} \cos \varphi}{R_{M}+h}-\frac{v_{E} \sec ^{2} \varphi}{\left(R_{M}+h\right)\left(R_{N}+h\right)} & 0 & -\frac{v_{E} \tan \varphi}{\left(R_{N}+h\right)^{2}}\end{array}\right] Fϕr= −RM+hωesinφ0−RM+hωecosφ−(RM+h)(RN+h)vEsec2φ000(RN+h)2vE−(RM+h)2vN−(RN+h)2vEtanφ
temp.setZero();
temp(0, 0) = -WGS84_WIE * sin(pvapre_.pos[0]) / rmh;
temp(0, 2) = pvapre_.vel[1] / rnh / rnh;
temp(1, 2) = -pvapre_.vel[0] / rmh / rmh;
temp(2, 0) = -WGS84_WIE * cos(pvapre_.pos[0]) / rmh - pvapre_.vel[1] / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(2, 2) = -pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh / rnh;
F.block(PHI_ID, P_ID, 3, 3) = temp;
F ϕ v = [ 0 1 R N + h 0 − 1 R M + h 0 0 0 − tan φ R N + h 0 ] \mathbf{F}_{\phi v}=\left[\begin{array}{ccc}0 & \frac{1}{R_{N}+h} & 0 \\ -\frac{1}{R_{M}+h} & 0 & 0 \\ 0 & -\frac{\tan \varphi}{R_{N}+h} & 0\end{array}\right] Fϕv= 0−RM+h10RN+h10−RN+htanφ000
temp.setZero();
temp(0, 1) = 1 / rnh;
temp(1, 0) = -1 / rmh;
temp(2, 1) = -tan(pvapre_.pos[0]) / rnh;
F.block(PHI_ID, V_ID, 3, 3) = temp;
IMU零偏误差和比例因子误差,建模成一阶高斯-马尔科夫过程,:
−
1
T
g
s
I
3
×
3
\frac{-1}{T_{g s}} \mathbf{I}_{3 \times 3}
Tgs−1I3×3
// IMU零偏误差和比例因子误差,建模成一阶高斯-马尔科夫过程
// imu bias error and scale error, modeled as the first-order Gauss-Markov process
F.block(BG_ID, BG_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(BA_ID, BA_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(SG_ID, SG_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(SA_ID, SA_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
然后构建系统噪声驱动矩阵:
G
18
21
×
18
=
[
0
0
0
0
0
0
C
b
n
0
0
0
0
0
0
C
b
n
0
0
0
0
0
0
I
3
×
3
0
0
0
0
0
0
I
3
×
3
0
0
0
0
0
0
I
3
×
3
0
0
0
0
0
0
I
3
×
3
]
\underset{21 \times 18}{\mathbf{G}_{18}}=\left[\begin{array}{cccccc}\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{C}_{b}^{n} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{C}_{b}^{n} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{I}_{3 \times 3} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}_{3 \times 3} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}_{3 \times 3} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}_{3 \times 3}\end{array}\right]
21×18G18=
0Cbn0000000Cbn0000000I3×30000000I3×30000000I3×30000000I3×3
// 系统噪声驱动矩阵
// system noise driven matrix
G.block(V_ID, VRW_ID, 3, 3) = pvapre_.att.cbn;
G.block(PHI_ID, ARW_ID, 3, 3) = pvapre_.att.cbn;
G.block(BG_ID, BGSTD_ID, 3, 3) = Eigen::Matrix3d::Identity();
G.block(BA_ID, BASTD_ID, 3, 3) = Eigen::Matrix3d::Identity();
G.block(SG_ID, SGSTD_ID, 3, 3) = Eigen::Matrix3d::Identity();
G.block(SA_ID, SASTD_ID, 3, 3) = Eigen::Matrix3d::Identity();
系统传播噪声的状态转移矩阵:
Φ
k
/
k
−
1
=
I
+
F
k
−
1
Δ
t
k
\boldsymbol{\Phi}_{k / k-1}=\boldsymbol{I}+\boldsymbol{F}_{k-1} \Delta t_{k}
Φk/k−1=I+Fk−1Δtk
// 状态转移矩阵
// compute the state transition matrix
Phi.setIdentity();
Phi = Phi + F * imucur.dt;
系统传播噪声:
Q
k
=
(
Φ
k
/
k
−
1
G
k
−
1
q
k
−
1
G
k
−
1
T
Φ
k
/
k
−
1
T
+
G
k
q
k
G
k
T
)
Δ
t
k
/
2
\boldsymbol{Q}_{k}=\left(\begin{array}{c}\boldsymbol{\Phi}_{k / k-1} \boldsymbol{G}_{k-1} \boldsymbol{q}_{k-1} \boldsymbol{G}_{k-1}^{T} \boldsymbol{\Phi}_{k / k-1}^{T} \\ +\boldsymbol{G}_{k} \boldsymbol{q}_{k} \boldsymbol{G}_{k}^{T}\end{array}\right) \Delta t_{k} / 2
Qk=(Φk/k−1Gk−1qk−1Gk−1TΦk/k−1T+GkqkGkT)Δtk/2
// 计算系统传播噪声
// compute system propagation noise
Qd = G * Qc_ * G.transpose() * imucur.dt;
Qd = (Phi * Qd * Phi.transpose() + Qd) / 2;
EKF 预测传播系统协方差和系统误差状态:
x
k
/
k
−
1
=
Φ
k
/
k
−
1
x
k
−
1
P
k
/
k
−
1
=
Φ
k
/
k
−
1
P
k
−
1
Φ
k
/
k
−
1
T
+
Q
k
\begin{aligned} \boldsymbol{x}_{k / k-1} & =\boldsymbol{\Phi}_{k / k-1} \boldsymbol{x}_{k-1} \\ \boldsymbol{P}_{k / k-1} & =\boldsymbol{\Phi}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{\Phi}_{k / k-1}^{T}+\boldsymbol{Q}_{k}\end{aligned}
xk/k−1Pk/k−1=Φk/k−1xk−1=Φk/k−1Pk−1Φk/k−1T+Qk
如果误差反馈了,那 x 应该是 0 ,无须再计算。
EKFPredict(Phi, Qd);
void GIEngine::EKFPredict(Eigen::MatrixXd &Phi, Eigen::MatrixXd &Qd) {
assert(Phi.rows() == Cov_.rows());
assert(Qd.rows() == Cov_.rows());
// 传播系统协方差和误差状态
// propagate system covariance and error state
Cov_ = Phi * Cov_ * Phi.transpose() + Qd;
dx_ = Phi * dx_;
}
八、GNSS 量测更新、系统状态反馈
1、gnssUpdate():GNSS 量测更新
先将 IMU 位置 pvacur_.pos 转到 GNSS 天线相位中心位置 antenna_pos:
r
^
G
=
r
^
I
+
D
R
−
1
C
^
b
n
l
b
\hat{\boldsymbol{r}}_{G}=\hat{\boldsymbol{r}}_{I}+\boldsymbol{D}_{R}^{-1} \hat{\boldsymbol{C}}_{b}^{n} \boldsymbol{l}^{b}
r^G=r^I+DR−1C^bnlb
// IMU位置转到GNSS天线相位中心位置
// convert IMU position to GNSS antenna phase center position
Eigen::Vector3d antenna_pos;
Eigen::Matrix3d Dr, Dr_inv;
Dr_inv = Earth::DRi(pvacur_.pos);
Dr = Earth::DR(pvacur_.pos);
antenna_pos = pvacur_.pos + Dr_inv * pvacur_.att.cbn * options_.antlever;
计算位置观测向量:IMU 预测天线位置减去 GNSS 观测位置,得到经纬高的差值,乘以
D
R
D_R
DR 转为 NED 差值:
z
r
=
D
R
(
r
^
G
−
r
~
G
)
\boldsymbol{z}_{r}=\boldsymbol{D}_{R}\left(\hat{\boldsymbol{r}}_{G}-\tilde{\boldsymbol{r}}_{G}\right)
zr=DR(r^G−r~G)
// GNSS位置测量新息
// compute GNSS position innovation
Eigen::MatrixXd dz;
dz = Dr * (antenna_pos - gnssdata.blh);
构造 GNSS 位置观测矩阵,姿态处是姿态乘以杆臂误差,位置处是单位阵:
H
r
=
[
I
3
0
3
(
C
b
n
l
b
)
×
0
3
0
3
0
3
0
3
]
\boldsymbol{H}_{r}=\left[\begin{array}{lllllll}\boldsymbol{I}_{3} & 0_{3} & \left(\boldsymbol{C}_{b}^{n} \boldsymbol{l}^{b}\right) \times & 0_{3} & 0_{3} & 0_{3} & 0_{3}\end{array}\right]
Hr=[I303(Cbnlb)×03030303]
// 构造GNSS位置观测矩阵
// construct GNSS position measurement matrix
Eigen::MatrixXd H_gnsspos;
H_gnsspos.resize(3, Cov_.rows());
H_gnsspos.setZero();
H_gnsspos.block(0, P_ID, 3, 3) = Eigen::Matrix3d::Identity();
H_gnsspos.block(0, PHI_ID, 3, 3) = Rotation::skewSymmetric(pvacur_.att.cbn * options_.antlever);
位置观测噪声阵,就是用数据文件中读取到的 GNSS 位置标准差平方得到协方差,组成成协方差阵:
// 位置观测噪声阵
// construct measurement noise matrix
Eigen::MatrixXd R_gnsspos;
R_gnsspos = gnssdata.std.cwiseProduct(gnssdata.std).asDiagonal();
得到观测向量 z,观测矩阵 H, 观测噪声矩阵 R 后,调用 EKFUpdate(),量测更新:
EKFUpdate(dz, H_gnsspos, R_gnsspos);
最后,GNSS更新之后设置为不可用:
gnssdata.isvalid = false;
2、EKFUpdate():EKF 更新协方差和误差状态
判断矩阵维度是否合理,不合理直接退出程序:
这几行 assert 可能是为了调试方便,能显示出哪两个矩阵维数不对。
assert(H.cols() == Cov_.rows());
assert(dz.rows() == H.rows());
assert(dz.rows() == R.rows());
assert(dz.cols() == 1);
计算 Kalman 滤波增益系数 K:
K
k
=
P
k
/
k
−
1
H
k
T
(
H
k
P
k
/
k
−
1
H
k
T
+
R
k
)
−
1
\boldsymbol{K}_{k}=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{T}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{T}+\boldsymbol{R}_{k}\right)^{-1}
Kk=Pk/k−1HkT(HkPk/k−1HkT+Rk)−1
// 计算Kalman增益
// Compute Kalman Gain
auto temp = H * Cov_ * H.transpose() + R;
Eigen::MatrixXd K = Cov_ * H.transpose() * temp.inverse();
更新系统误差状态和协方差:
P
k
=
(
I
−
K
k
H
k
)
P
k
/
k
−
1
(
I
−
K
k
H
k
)
T
+
K
k
R
k
K
k
T
K
k
=
P
k
/
k
−
1
H
k
T
(
H
k
P
k
/
k
−
1
H
k
T
+
R
k
)
−
1
\begin{array}{l}\boldsymbol{P}_{k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1}\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right)^{T}+\boldsymbol{K}_{k} \boldsymbol{R}_{k} \boldsymbol{K}_{k}^{T} \\ \boldsymbol{K}_{k}=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{T}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{T}+\boldsymbol{R}_{k}\right)^{-1}\end{array}
Pk=(I−KkHk)Pk/k−1(I−KkHk)T+KkRkKkTKk=Pk/k−1HkT(HkPk/k−1HkT+Rk)−1
// 更新系统误差状态和协方差
// update system error state and covariance
Eigen::MatrixXd I;
I.resizeLike(Cov_);
I.setIdentity();
I = I - K * H;
// 如果每次更新后都进行状态反馈,则更新前dx_一直为0,下式可以简化为:dx_ = K * dz;
// if state feedback is performed after every update, dx_ is always zero before the update
// the following formula can be simplified as : dx_ = K * dz;
dx_ = dx_ + K * (dz - H * dx_);
Cov_ = I * Cov_ * I.transpose() + K * R * K.transpose();
3、stateFeedback():状态反馈
想清楚卡尔曼滤波到底算的是什么,考虑到底是加还是减。零偏、比例因子残差是加、速度位置残差是减,反馈之后误差状态置 0:
- 位置反馈要乘以
DRi(),因为估计的位置增量是 ENU,要转为 LLH 增量。 - 姿态反馈首先要把算出的等效旋转矢量增量转为四元数,然后左乘这个四元数。
void GIEngine::stateFeedback() {
Eigen::Vector3d vectemp;
// 位置误差反馈
// posisiton error feedback
Eigen::Vector3d delta_r = dx_.block(P_ID, 0, 3, 1);
Eigen::Matrix3d Dr_inv = Earth::DRi(pvacur_.pos);
pvacur_.pos -= Dr_inv * delta_r;
// 速度误差反馈
// velocity error feedback
vectemp = dx_.block(V_ID, 0, 3, 1);
pvacur_.vel -= vectemp;
// 姿态误差反馈
// attitude error feedback
vectemp = dx_.block(PHI_ID, 0, 3, 1);
Eigen::Quaterniond qpn = Rotation::rotvec2quaternion(vectemp);
pvacur_.att.qbn = qpn * pvacur_.att.qbn;
pvacur_.att.cbn = Rotation::quaternion2matrix(pvacur_.att.qbn);
pvacur_.att.euler = Rotation::matrix2euler(pvacur_.att.cbn);
// IMU零偏误差反馈
// IMU bias error feedback
vectemp = dx_.block(BG_ID, 0, 3, 1);
imuerror_.gyrbias += vectemp;
vectemp = dx_.block(BA_ID, 0, 3, 1);
imuerror_.accbias += vectemp;
// IMU比例因子误差反馈
// IMU sacle error feedback
vectemp = dx_.block(SG_ID, 0, 3, 1);
imuerror_.gyrscale += vectemp;
vectemp = dx_.block(SA_ID, 0, 3, 1);
imuerror_.accscale += vectemp;
// 误差状态反馈到系统状态后,将误差状态清零
// set 'dx' to zero after feedback error state to system state
dx_.setZero();
}
九、KF-GINS常见问题
复制自 PPT
KF-GINS能够达到怎么样的定位精度?
组合导航算法精度更受IMU等级、以及测试时GNSS定位质量影响。组合导航算法相对成熟,对于同样的设备只要算法正确实现,算法几乎不会对定位精度产生较大影响。
初始导航状态和初始导航状态标准差如何给定?
-
初始位置(和速度)可由GNSS给定,初始姿态(和速度)可从参考结果中获取;
-
位置速度标准差可由GNSS给定,姿态标准差可给经验值,车载领域一般横滚俯仰小,航向大一些
IMU数据输入到程序之前,需要扣除重力加速度吗?
不需要,惯性导航算法中补偿了重力加速度
INS机械编排中旋转效应等补偿项,对于低端IMU是否需要补偿?
低端IMU测量噪声更大,简化的IMU积分算法对低端IMU精度产生的影响较小
组合导航中GNSS信号丢失期间进行纯惯导解算,这时IMU误差项可以补偿吗?
GNSS丢失期间IMU误差项不更新,但是可以利用之前估计的IMU误差项继续补偿
IMU数据,如何从速率形式转到增量形式?
一般采用更高频率速率数据积分得到增量数据,参考:新手入门系列4——MEMS IMU原始数据采集和时间同步的那些坑(i2Nav网站)
IMU零偏和比例因子建模时相关时间如何给定?
建模为一阶高斯-马尔可夫过程,实际中一般根据经验设置相关时间,MEMS设置1h
GNSS/INS组合导航中是否需要考虑惯性系和车体系的转换?
不需要,GNSS/INS组合导航不受载体限制,不需要考虑车体系
初始化拓展
-
动态初始对准,GNSS位置差分速度(或者GNSS直接输出速度),位置差分计算初始航向
-
快速航向初始化 ,轨迹匹配方法快速获取准确初始航向
-
静态粗对准,适用于高精度惯导,双矢量法找到初始姿态
观测信息拓展
-
直接构建观测向量、观测模型和噪声矩阵,调用EKFUpdate更新和stateFeedback反馈
-
GNSS速度观测信息、NHC约束信息(对于车载)、零速信息修正
状态信息拓展
- 如果需要增广系统状态(如里程计增广比例因子[2]),则修改RANK(NOISERANK),添加StateID, NoiseID
- 协方差、状态转移矩阵、观测信息对应修改;添加观测信息,进行更新反馈