什么是贪心?
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。 贪心没有规定的套路。
刷题或面试的时候,手动模拟一下感觉可以局部最优退出整体最优,而且想不到反例,那么就试一试贪心。 贪心算法一般分为如下四步:
将问题分为若干子问题 找出合适的贪心策略 求解每一个子问题的最优解 将局部最优解堆叠成全局最优解
方法1: 充分利用每个饼干的大小,用大块的饼干优先喂饱大胃口的孩子
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(),g.end());
sort(s.begin(),s.end());
int ret = 0;
int cookie_index = s.size()-1;//饼干下标
for(int i = g.size() - 1; i >= 0; i--){// 遍历孩纸
// >= 0说明还有饼干
if(cookie_index >= 0 && s[cookie_index] >= g[i]){
ret++;
cookie_index--;
}
}
return ret;
}
};
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(),g.end());
sort(s.begin(),s.end());
int ret = 0;
int kid_index = 0;//饼干下标
for(int i = 0; i < s.size(); i++){// 遍历饼干
if(kid_index < g.size() && s[i] >= g[kid_index]){
kid_index++;
}
}
return kid_index;
}
};
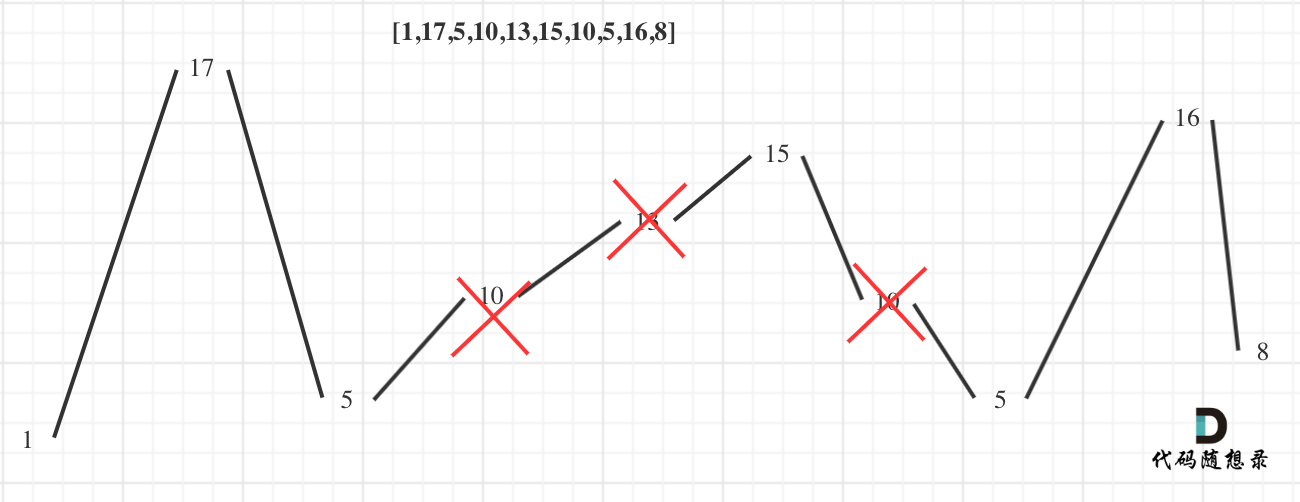
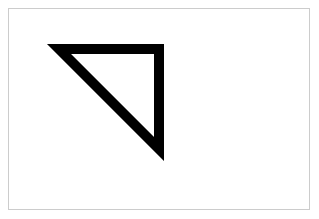
注意: 子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
关键词: 波峰波谷 如下图所示:
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
int n = nums.size();
if(n <= 1)return n;
int curDiff = 0;// 当前一对差值
int preDiff = 0;// 前一对差值
int ret = 1;// 默认在左右两侧会有一侧有一个峰值
for(int i = 0; i < n-1; i++){
curDiff = nums[i+1] - nums[i];
// 出现峰值-注意=0情况
if((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)){
ret++;
preDiff = curDiff;
}
}
return ret;
}
};
方法2: dp 每个元素,不是波峰,就是波谷
dp数组含义:
dp[i][0]表示以当前元素为山谷,最长摆动子序列的长度 dp[i][1]表示以当前元素为山峰,最长摆动子序列的长度 状态转移方程:
dp[i][0] = max(dp[i][0],dp[j][1]+1)
0 < j < i ,num[j] > num[i] 表示将nums[i]接到前面某个山峰的后面,作为山谷 dp[i][1] = max(dp[i][1],dp[j][0]+1)
0 < j < i, num[j] < num[i] 表示将nums[i]接到前面某个山谷的后面,作为山峰 初识状态:
一个数可以接前面某个数的后面,也可以以自身作为子序列的起点,所以初始化为: dp[0][0] = 1 dp[0][1] = 1 以第一个点作为山峰or谷都初始化为1,与上面贪心方法初始ret=1同理
// 时间复杂度O(n^2)
// 空间复杂度O(n)
class Solution {
public:
int dp[1001][2];
int wiggleMaxLength(vector<int>& nums) {
memset(dp,0,sizeof(dp));
dp[0][0] = dp[0][1] = 1;
for(int i = 1; i < nums.size();i++){
dp[i][0]=dp[i][1]=1;
for(int j = 0; j < i;j++){
// 当前点可以作为波谷接到前一个元素后面
if(nums[j] > nums[i])dp[i][0] = max(dp[i][0],dp[j][1]+1);
}
for(int j = 0; j < i;j++){
// 当前点可以作为波峰接到前一个元素的后面
if(nums[j] < nums[i])dp[i][1] = max(dp[i][1],dp[j][0]+1);
}
}
return max(dp[nums.size()-1][0],dp[nums.size()-1][1]);
}
};
方法1: 贪心方法,当当前累加和为负数时,终止累加。
// 时间复杂度O(n)
// 空间复杂度O(1)
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int ret = INT_MIN;
int tmp = 0;
for(int i = 0;i < nums.size() ;i++){
tmp += nums[i];
if(tmp > ret)ret = tmp;
if(tmp <= 0)tmp = 0;
}
return ret;
}
};
// 时间复杂度:O(n^2)
// 空间复杂度: O(1)
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int ret = INT_MIN;
int tmp = 0;
for(int i = 0;i < nums.size() ;i++){
tmp = 0;
for(int j = i ; j < nums.size();j++){
tmp += nums[j];
ret = max(tmp,ret);
}
}
return ret;
}
};
两天为一个单位进行利润的计算 贪心: 局部最优收集每天的正利润,求得全局最优的最大利润
// 时间复杂度:O(n)
// 空间复杂度:O(1)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int ret =0;
for(int i = 1; i < prices.size();i++){
ret += max(prices[i]-prices[i-1],0);
}
return ret;
}
};
动态规划
dp数组含义,dp[i][0],持有当天股票所获的最多现金,dp[i][1]持有的最多现金数
class Solution {
public:
int maxProfit(vector<int>& prices) {
vector<vector<bool>>dp(prices.size(),vector<bool>(2,0))
dp[0][0] -= prices[0];
dp[0][1] = 0;
for(int i = 1; i < prices.size();i++){
// 当天持有股票后所获得的最多现金——买入
dp[i][0] = max(dp[i-1][1]-prices[i],dp[i-1][0])
// 当天所持有的最多现金,前一天的最多现金和在当天卖出做比较——卖出
dp[i][1] = max(dp[i-1][1],dp[i-1][0]+prices[i])
}
}
};
贪心: 每次取最大跳跃步数,即最大的可覆盖范围,整体最优,最后得到最大的覆盖范围,判断是否可以到达终点
class Solution {
public:
bool canJump(vector<int>& nums) {
int n = nums.size();
int cover = 0;
if(n == 1)return true;
for(int i = 0; i <= cover ;i++){// for循环控制当前可走到的范围
cover = max(i+nums[i],cover);// 尝试更新当前可覆盖的范围
if(cover >= n-1)return true;
}
return false;
}
};
贪心
每一步都走到可以到达的最远位置,求得最小步数,就是全局最优。
其中不用管具体是怎么跳的,不用纠结到底是跳几个单位。
class Solution {
public:
int jump(vector<int>& nums) {
int n = nums.size();
if(n == 1)return 0;
int curCover = 0;// 当前最大可到达的范围
int nextCover = 0;// 下一步可到达的最大范围
int cnt = 0;// 步数
for(int i = 0; i < n;i++){
nextCover = max(nums[i]+i,nextCover);// 更新下一步最远覆盖的距离
if(i == curCover){// 到了当前可以走的最远位置了,也就是要走一步了
if( curCover != n-1){// 还没到终点
cnt++;// 走了一步
curCover = nextCover;// 更新当前可到达的最远下标
if(curCover >= n-1)break;// 剪枝-当前覆盖范围已经到达
}else break;//到达终点
}
}
return cnt;
}
};
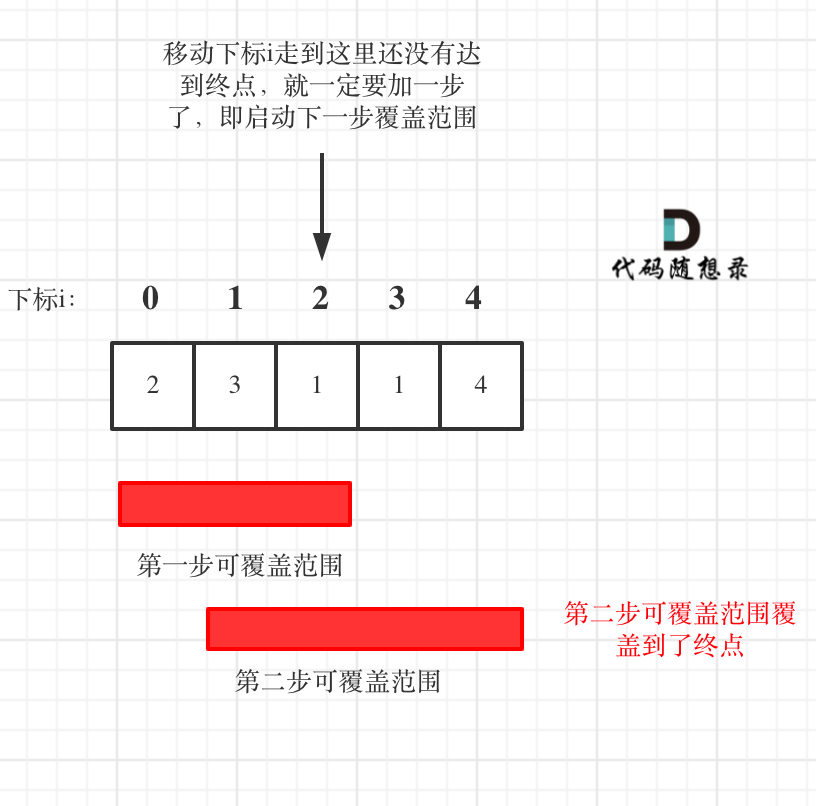
方法2,简化方法1
移动下标只要遇上最远距离的下标,就直接再走一步,这样的前提是,我们让下标移动的最远位置定为n-2,因为到了倒数第二个,我们再走一步肯定就到真正的结尾了。题目假设总是可以到达最后一个位置。
class Solution {
public:
int jump(vector<int>& nums) {
int cnt = 0;
int curCover = 0;
int nextCover =0;
int n = nums.size();
if(n == 1)return 0;
for(int i = 0; i < n-1;i++){// n-1是关键
nextCover = max(nums[i]+i,nextCover);//更新下一步最远覆盖距离
if(i == curCover){
curCover = nextCover;
cnt++;
}
}
return cnt;
}
};
贪心:
局部最优: 让绝对值大的负数变为正数,当前值达到最大
再次贪心,如果已经将所有负数都变为正数了,将剩余的k全作用在最小值上。以保证全局最大值 整体最优: 使得整个数组和达到最大值
class Solution {
public:
static bool cmp(int a,int b){
return abs(a) > abs(b);
}
int largestSumAfterKNegations(vector<int>& nums, int k) {
sort(nums.begin(),nums.end(),cmp);
for(int i = 0; i < nums.size();i++){
if(nums[i] < 0 && k > 0){
nums[i] = -nums[i];
k--;
}
}
// 将所有负数都变为正数后还有剩余的k,那么就反复反转数值最小的
// 偶数个反转后不变,奇数个变为负
if(k % 2)nums[nums.size()-1] *= -1;
return accumulate(nums.begin(),nums.end(),0);
}
};
// 时间复杂度O(n);
// 空间复杂度O(1)
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int curSum = 0;
int min = INT_MAX;
for(int i = 0; i < gas.size();i++){
int rest = gas[i] - cost[i];
curSum += rest;
if(curSum < min)min = curSum;
}
if(curSum < 0)return -1;// 无论从哪个点出发都不行
if(min >= 0)return 0;// 从开头出发,油就没断过
// 累加的最小值是负数,放从后往前出发,看哪个位置可以把这个值填平
for(int i = gas.size()-1;i >= 0;i--){
int rest = gas[i] - cost[i];
min += rest;
if(min >= 0)return i;
}
return -1;
}
};
贪心: 方法2
局部最优: 如果当前累加的剩余油量<0,起始位置至少是i+1(总的累加剩余量>0) 全局最优: 可以找到起始位置
// 时间复杂度O(n)
// 空间复杂度O(1)
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int curSum = 0;
int totalSum = 0;
int start = 0;
for(int i = 0; i < gas.size();i++){
curSum += gas[i] - cost[i];
totalSum += gas[i] - cost[i];
if(curSum < 0){
start = i + 1;// 更新起始位置,后面有更大的正数,前提是totalSum > 0,即存在这个一个可行的位置
curSum = 0;
}
}
if(totalSum < 0)return -1;// 怎么走都不够,则后面没有更大的正数
return start;
}
};
// 时间复杂度O(n^2)
// 空间复杂度O(1)
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
for(int i = 0; i < gas.size();i++){
int rest = gas[i]-cost[i];
int index = (i+1) % cost.size();// 下一个结点
while(rest > 0 && index != i){// 从i开始模拟一圈
rest += gas[index] - cost[index];
index = (index+1) % gas.size();
}
if(rest >=0 && index == i)return i;// >=0 并且最终到达i
}
return -1;
}
};
注意: 要分左边大于右边,和右边大于左边情况分别讨论 局部最优: 分情况分别讨论出每个孩子所需要的糖果。评论高的孩子获得更多的糖果 全局最优: 至少所需要的糖果数
class Solution {
public:
int candy(vector<int>& ratings) {
vector<int>candyVec(ratings.size(),1);
// 从前往后遍历,判断右 > 左情况
for(int i = 1; i < ratings.size();i++){
if(ratings[i] > ratings[i-1])candyVec[i] = candyVec[i-1]+1;
}
// 从后往前遍历,判断左 > 右情况
for(int i = ratings.size() - 2;i >= 0;i--){
// 注意遍历顺序以及判断方式,利用到前一步判断出来的结果
if(ratings[i] > ratings[i+1]){
// 注意这里的max,情况为,当前这个孩子既大于左边又大于右边
// candyVec[i]为上面求出大于左边情况
// candyVec[i+1]+1为这个for中大于右边情况
// 选多的,兼顾左右
candyVec[i] = max(candyVec[i],candyVec[i+1]+1);
}
}
return accumulate(candyVec.begin(),candyVec.end(),0);
}
};
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
int twenty = 0;
int ten = 0;
int five = 0;
for(int& bill:bills){
// 5块的
if(bill == 5)five++;
// 10块的
if(bill == 10){
if(five <= 0)return false;
five--;
ten++;
}
// 20块的
if(bill == 20){
// 优先消耗10+5
if(ten >0 && five > 0){
ten--;
five--;
twenty++;
}else if(five >= 3){
five -= 3;
twenty++;
}else return false;
}
}
return true;
}
};
贪心:
局部最优: 按身高排序后,优先按照身高高的k插入,插入操作过后的people满足队列属性 全局最优: 最后都做完插入操作,整个队列满足该属性
// 时间复杂度 O(n+logn +n ^ 2)
// 空间复杂度 O(n)
class Solution {
public:
static bool cmp(vector<int>& a,vector<int>& b){
if(a[0] == b[0])return a[1] < b[1];// k叫大的放后面
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
// 权衡两个维度的时候,先确定一个再确定另一个
sort(people.begin(),people.end(),cmp);
vector<vector<int>>ret;
for(int i = 0; i < people.size();i++){
int pos = people[i][1];
ret.insert(ret.begin()+pos,people[i]);
}
return ret;
}
};
class Solution {
public:
static bool cmp(vector<int>& a,vector<int>& b){
if(a[0] == b[0])return a[1] < b[1];// k叫大的放后面
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
// 权衡两个维度的时候,先确定一个再确定另一个
sort(people.begin(),people.end(),cmp);
list<vector<int>>que;
for(int i = 0; i < people.size();i++){
int pos = people[i][1];
list<vector<int>>::iterator it = que.begin();
while(pos--)it++;// 寻找查找位置
que.insert(it,people[i]);
}
return vector<vector<int>>(que.begin(),que.end());
}
};
手动模拟vector插入过程,不让其底层自己扩容,提高效率(不一定)
class Solution {
public:
static bool cmp(vector<int>& a,vector<int>& b){
if(a[0] == b[0])return a[1] < b[1];// k叫大的放后面
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
// 权衡两个维度的时候,先确定一个再确定另一个
sort(people.begin(),people.end(),cmp);
vector<vector<int>>ret(people.size(),vector<int>(2,-1));
for(int i = 0; i < people.size();i++){
int pos = people[i][1];
if(pos == ret.size()-1)ret[pos] = people[i];
for(int j = people.size()-2;j>=pos;j--)ret[j+1] = ret[j];
ret[pos] = people[i];
}
return ret;
}
};
贪心:
局部最优: 尽可能将气球覆盖到一起,用越少的箭射爆 全局最优: 得出最少需要的箭
// 时间复杂度 O(nlogn)
// 空间复杂度 O(1)
class Solution {
public:
// 根据起始坐标进行排序
static bool cmp(vector<int>& a,vector<int>&b){
return a[0] < b[0];
}
int findMinArrowShots(vector<vector<int>>& points) {
if(points.size() == 0)return 0;
sort(points.begin(),points.end(),cmp);
int ret = 1;// 最少需要一支箭
for(int i = 1; i < points.size();i++){
if(points[i][0] > points[i-1][1])ret++;// 两个气球无法覆盖了,需要一支箭,注意没有=,因为=也是可以射爆的
else points[i][1] = min(points[i][1],points[i-1][1]);// 更新重叠气球右侧最小边界
}
return ret;
}
};
不知道是不是用例更新还是怎么了,提交了提示通过了所有用例,但是还是超时了 按照右边界进行排序,从左往右遍历,右边界越小越好 贪心:
局部最优:优先选取右边界小的区间,从左往右遍历,留给下一个空间大一些,从而尽量避免交叉。 全局最优:选取最多的非交叉区间,要删除的交叉区间用总数减去非交叉区间即可。
// 时间复杂度O(nlogn)
// 空间复杂度O(n)
class Solution {
public:
static bool cmp(vector<int>a,vector<int>b){
return a[1] < b[1];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if(intervals.size() == 0)return 0;
sort(intervals.begin(),intervals.end(),cmp);
int cnt = 1;// 记录非交叉区间的个数
int end = intervals[0][1];
for(int i = 1; i < intervals.size() ;i++){
if(intervals[i][0] >= end){
end = intervals[i][1];
cnt++;
}
}
return intervals.size() - cnt;
}
};
// 时间复杂度O(nlogn)
// 空间复杂度O(n)
class Solution {
public:
static bool cmp(vector<int>a,vector<int>b){
return a[0] < b[0];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if(intervals.size() == 0)return 0;
sort(intervals.begin(),intervals.end(),cmp);
int cnt = 1;// 记录非交叉区间的个数
int start = intervals[intervals.size()-1][0];
for(int i = intervals.size()-2; i >= 0 ;i--){
if(start >= intervals[i][1]){
start = intervals[i][0];
cnt++;
}
}
return intervals.size() - cnt;
}
};
// 时间复杂度O(nlogn)
// 空间复杂度O(n)
class Solution {
public:
static bool cmp(vector<int>a,vector<int>b){
return a[0] < b[0];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if(intervals.size() == 0)return 0;
sort(intervals.begin(),intervals.end(),cmp);
int cnt = 1;// 记录非交叉区间的个数
for(int i = 1; i < intervals.size() ;i++){
if(intervals[i][0] >= intervals[i-1][1]){
cnt++;
}else intervals[i][1] = min(intervals[i][1],intervals[i-1][1]);// 取小的,因为在后序的判断中,如果小与这个,说明还在前面的覆盖范围内
}
return intervals.size() - cnt;
}
};
哈希,还挺有意思,到达了某个出现较靠后的字符,就收集。
// 时间复杂度O(n)
// 空间复杂度O(1)
class Solution {
public:
vector<int> partitionLabels(string s) {
unordered_map<char,int>mp;
for(int i = 0; i < s.size();i++)mp[s[i]] = i;// 记录字符最后出现的位置
vector<int>ret;
int left = 0;
int right = 0;
for(int i = 0; i < s.size();i++){
right = max(right,mp[s[i]]);// 到了某个出现较靠后的字符
if(i == right){
ret.push_back(right - left + 1);
left = i + 1;
}
}
return ret;
}
};
贪心:
局部最优: 每次合并都取最大右边界,合并更多区间 全局最优: 合并所有重叠的区间
// 时间复杂度O(nlogn)
// 空间复杂度O(n)
class Solution {
public:
static bool cmp(vector<int>& a,vector<int>& b){
return a[0] < b[0];
}
vector<vector<int>> merge(vector<vector<int>>& intervals) {
vector<vector<int>>ret;
int n = intervals.size();
if(n == 0)return ret;
sort(intervals.begin(),intervals.end(),cmp);
ret.push_back(intervals[0]);// 先放入第一个结点
for(int i = 1; i < n;i++){
if(intervals[i][0] <= ret.back()[1]){// 合并区间
ret.back()[1] = max(ret.back()[1],intervals[i][1]);
}else ret.push_back(intervals[i]);
}
return ret;
}
};
贪心
局部最优: 遇到非递增情况,将前一个数–,当前位置为9,保证这两位去单调递增
实际操作的时候,用flag来记录从哪开始将值都置为9 全局最优: 得到小于等于n的单调递增整数
// 时间复杂度O(n)
// 空间复杂度O(n)
class Solution {
public:
int monotoneIncreasingDigits(int n) {
string str = to_string(n);
int flag = -1;
// 从后往前遍历,用到后面已经比较得出的结果
for(int i = str.size() -1 ;i > 0;i--){
if(str[i-1] > str[i]){
flag = i;
str[i-1]--;
}
}
for(int i = flag; i < str.size();i++){
str[i] = '9';
}
return stoi(str);
}
};
// 时间复杂度O(m*n)
// 空间复杂度O(1)
class Solution {
public:
int check_num(int num){
int max = 10;
// 1234
while(num){
int t = num % 10;
if(max >= t)max = t;
else return false;
num /= 10;
}
return true;
}
int monotoneIncreasingDigits(int n) {
for(int i = n; i >= 0;i--){
if(check_num(i))return i;
}
return 0;
}
};
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int minPrice= prices[0];
int ret = 0;
int n = prices.size();
for(int i = 1; i < n ; i++){
// 找到更小的买入日期
if(prices[i] < minPrice){
minPrice = prices[i];
continue;
}
// 不适合卖出,不够手续费,或没得赚。
// 其实下面这个if判断是可以删除的。
if(prices[i] > minPrice && prices[i] <= minPrice+fee)continue;
// 计算利润——————卖出,在卖出的时候去掉fee获得利润。
// 核心思想为,假买假卖,直到下一个更小的minPrice,确实上一个真的卖出了。
if(prices[i] > minPrice+fee){
// 现在更多的利润减去之前的利润,得到需要增加多少。
// 结合示例来看。
// prices = [1, 4, 2, 8, 4, 9], fee = 2
// 1的时候买入,4的时候我们计算了一次利润,此时minPrice = prices[i]-fee;
// 如果之后我们找到更小的minPrice,说明"前一个"的股票,到"昨天"为止,已经拿到了最大利润。
// 开始新的利润寻找,即开始新的买入与对应新的卖出。
ret += prices[i]-fee-minPrice;// 当前行代码解释如下:
// 为在找到下一个更小的minPrice之前,挣取可能的最大利润。
// 其实,下面的 prices[i]-fee也可以理解为:
// 这里减去一个fee,如果找到了更大的利润空间,当前的if判断条件中的"minPrice+fee"会加回来。
// 也就是说,这样进行比较的是,之前假卖的价格与现在的价格做对比。
// 如果大于,说明找到更大的卖出日期了。
// 执行prices[i]-fee-minPrice
// prices[i]-fee为当天卖出所获的纯利润,减去之前的纯利润。
// 即为,当天卖出比上次假卖要多获得多少利润。
// 累加到ret上,如果后续出现了更小的minPrice,说明之前的一波买卖已经完成了。
// 继续新的买卖....
minPrice = prices[i]-fee;
// 额外补充一些
// 如果后续没有比minPrice+fee要大的了,其实根本就不会进行利润判断,因为进不了这个if判断。
// 还有就是当前判断条件为prices[i] > minPrice+fee,这里并没有包括等于,等于的情况说明我们所获利润为0,也就是加不加都无所谓。
// 如果第一天买入了,后面根本就没有能卖出的天数,例如:
// prices = [1, 3, 3, 3, 3, 3], fee = 2
// 也就是为0,ret不会在此循环中进行加减操作。
// 最终返回ret,ret默认就是0,嘻嘻~。
}
}
return ret;
}
};
简化为
核心思想:遇到可赚的,先卖出,后面遇到更大的,补上利润,再遇到更小的,开启新一轮的买卖。
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
int minPrice = prices[0];
int ret = 0;
for(int i = 1; i < n;i++){
if(prices[i] < minPrice){
minPrice = prices[i];
continue;
}
if(prices[i] > minPrice + fee){
ret += prices[i]-fee-minPrice;
minPrice = prices[i]-fee;
}
}
return ret;
}
};
贪心:
尽可能的在非叶子结点放摄像头,使其辐射的范围大些。使得使用的摄像头数最少。
class Solution {
public:
// 0-该结点无覆盖 1-该结点有摄像头 2-该结点有覆盖
int ret;
int dfs(TreeNode* cur){
// 空结点
if(!cur)return 2;
int left = dfs(cur->left);
int right = dfs(cur->right);
// 左右结点都覆盖
if(left == 2 && right == 2)return 0;
// 有一个孩子没覆盖,该结点就要放摄像头
if(left == 0 || right == 0){
ret++;
return 1;
}
// 有一个孩子是摄像头,当前结点有覆盖
if(left == 1 || right == 1)return 2;
return -1;// 不会到这
}
int minCameraCover(TreeNode* root) {
ret = 0;
if(dfs(root) == 0){// 如果根节点没被覆盖,增加个摄像头
ret++;
}
return ret;
}
};
二刷贪心完成,这个月底要完成二刷代码随想录,要加油了。 如果明年1月有时间三刷我大概率不会总结了。