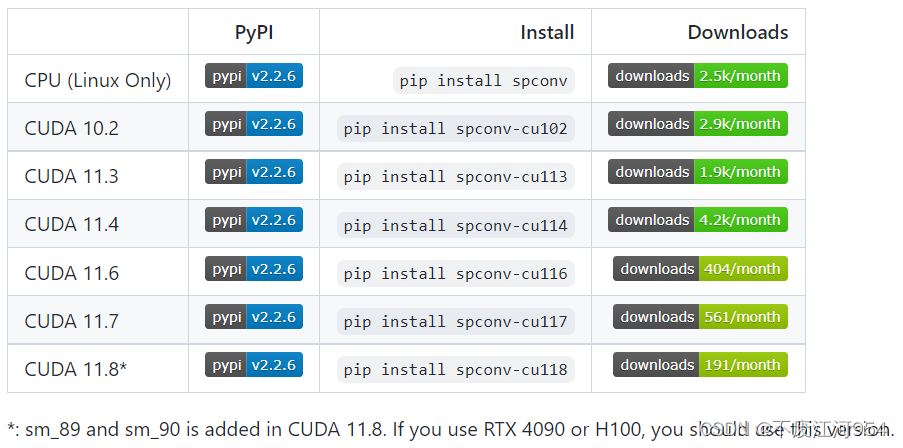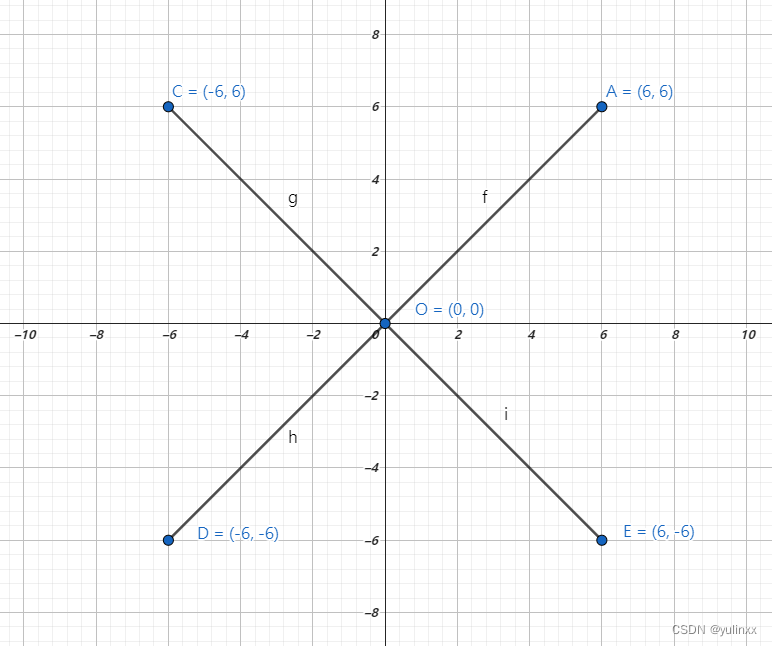
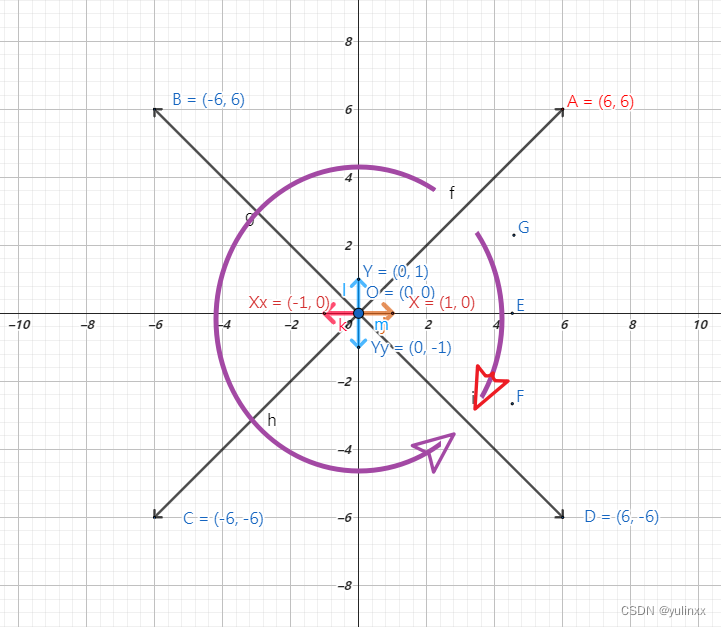
以 O 点为圆心, 绘制如上图,
则有向量 vOA, vOB, vOC, vOD
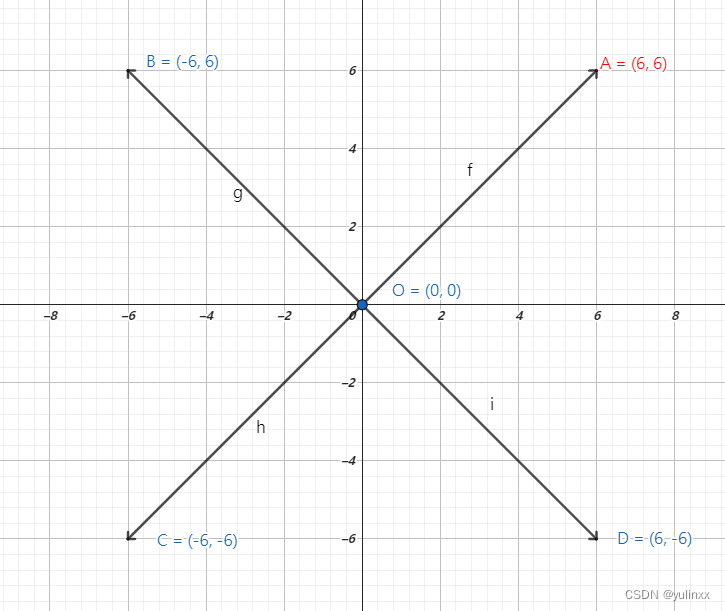
再给定一个X轴方向的单位向量 vX = [1, 0]
则 向量 vOA, vOB, vOC, vOD 分别与 vX 进行叉乘:
# python 代码
# X Y 轴上的单位向量
vX = [1, 0]
vY= [0, 1]
vA = [6, 6]
vB = [-6, 6]
vC = [-6, -6]
vD = [6, -6]
c1 = np.cross(vX, vA) # 逆时针 45 度
c2 = np.cross(vX, vB) # 逆时针 90 + 45 度
c3 = np.cross(vX, vC) # 逆时针 180 + 45 度
c4 = np.cross(vX, vD) # 逆时针 270 + 45 度
print(f'c1 {c1} c2 {c2} c3 {c3} c4 {c4}')
# c1 6 c2 6 c3 -6 c4 -6
d1 = np.dot(vX, vA) # 逆时针 45 度
d2 = np.dot(vX, vB) # 逆时针 90 + 45 度
d3 = np.dot(vX, vC) # 逆时针 180 + 45 度
d4 = np.dot(vX, vD) # 逆时针 270 + 45 度
print(f'd1 {d1} d2 {d2} d3 {d3} d4 {d4}')
# d1 6 d2 -6 d3 -6 d4 6
c5 = np.cross(vX, vY) # X与Y垂直
c6 = np.cross(vA, vD) # 垂直
c7 = np.cross(vA, vC) # 共线,方向相反
c8 = np.cross(vB, vD) # 共线,方向相反
print(f'c5 {c5} c6 {c6} c7 {c7} c8 {c8}')
# c5 1 c6 -72 c7 0 c8 0
d5 = np.dot(vX, vY) # X与Y垂直
d6 = np.dot(vA, vD) # 垂直
d7 = np.dot(vA, vC) # 共线,方向相反
d8 = np.dot(vB, vD) # 共线,方向相反
print(f'd5 {d5} d6 {d6} d7 {d7} d8 {d8}')
# d5 0 d6 0 d7 -72 d8 -72
结果为:
c1 6 c2 6 c3 -6 c4 -6
d1 6 d2 -6 d3 -6 d4 6
c5 1 c6 -72 c7 0 c8 0
d5 0 d6 0 d7 -72 d8 -72
向量之间的夹角是0~180
通过叉乘 (A, B),若结果为正,则B向量在A向量的逆时针方向,
若结果为负,则B向量在A向量的逆时针方向,如 OC向量
为零,则共线
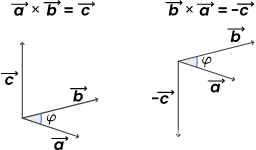
向量OA到向量OD 走大圆角还是小圆角
向量的点乘
dAD = np.dot(vA, vD)
dDA = np.dot(vD, vA)
print(f'dAD: {dAD}, dDA:{dDA}')
cAD = np.cross(vA, vD)
cDA = np.cross(vD, vA)
print(f'cAD: {cAD}, cDA: {cDA}')
# dAD: 0, dDA:0
# cAD: -72, cDA: 72
-
点乘
结果均一致,无法判断边的先后关系,
只能确定两边的夹角(0-180度内)关系:锐角 > 0,直角 = 0,钝角 < 0 -
叉乘
结果有正有负,通过右手法则可知,cAD 为负,则应该走上图中的小圆角
cDA结果为正,也符合右手法则,同样走小圆角
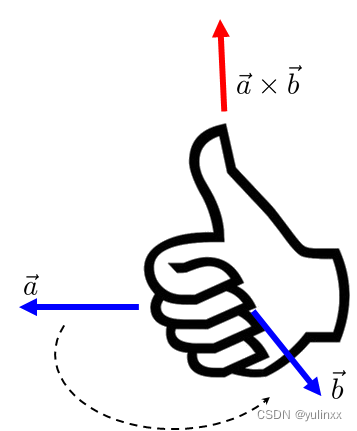
右手法则中,均为右手手指指向第一个向量的位置,然后,手指握拳的方向,指向小于180度方向的向量
使用:
可使用A B向量,通过点乘计算其夹角角度:
# 向量角度 方法1
def angle(v1, v2):
return math.acos(dotproduct(v1, v2) / (length(v1) * length(v2)))
# 向量角度 方法2
def angle_between(v1, v2):
""" Returns the angle in radians between vectors 'v1' and 'v2'::
>>> angle_between((1, 0, 0), (0, 1, 0))
1.5707963267948966
>>> angle_between((1, 0, 0), (1, 0, 0))
0.0
>>> angle_between((1, 0, 0), (-1, 0, 0))
3.141592653589793
"""
v1_u = unit_vector(v1)
v2_u = unit_vector(v2)
return np.arccos(np.clip(np.dot(v1_u, v2_u), -1.0, 1.0))
再通过叉乘, 得出其先后关系:
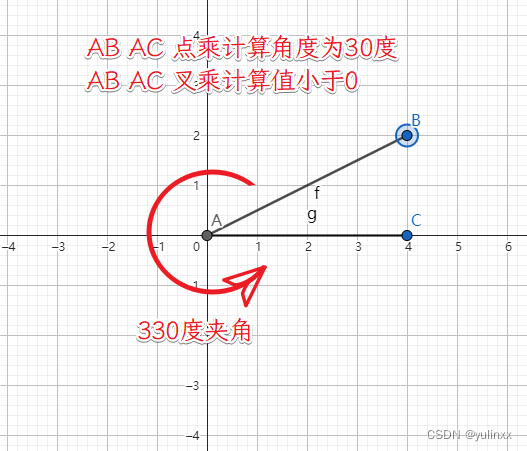
若得出的向量角度为30度,
- A与B叉乘,结果为负值 , 即B向量在A向量的顺时针方向
则AB间的夹角应为 360 - 30 = 330 度 - A与B叉乘,结果为正值 , 即B向量在A向量的逆时针方向
则AB间的夹角应为 360 - 30 = 330 度