题库链接:https://leetcode.cn/problem-list/e8X3pBZi/
| 类型 | 题目 | 解决方案 |
|---|---|---|
| 栈的应用 | 剑指 Offer II 036. 后缀表达式 | 模拟 + 栈 ⭐ |
| 剑指 Offer II 037. 小行星碰撞 | 分类讨论 + 栈 ⭐ | |
| 单调栈 | 剑指 Offer II 038. 每日温度 | 单调栈 ⭐ |
| 剑指 Offer II 039. 直方图最大矩形面积 | 单调栈 ⭐ | |
| 剑指 Offer II 040. 矩阵中的最大矩形 | 矩阵转化直方图 + 单调栈 ⭐ |
栈:后入后出,所以栈的插入和删除操作都发生在栈顶;
Java 中 Stack 的常用操作:
- push(e):元素 e 入栈;
- pop():位于栈顶的元素出栈,并返回该元素;
- peek():返回位于栈顶的元素,该元素不出栈;
1. 剑指 Offer II 036. 后缀表达式 – P93
根据 逆波兰表示法,求该后缀表达式的计算结果。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
1.1 模拟 + 栈 – O(n)(⭐)
时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( n ) O(n) O(n)
🎈 注意:该题是通过栈来保存操作数,但不保存运算符,通过对运算符的判断从而进行数值的模拟计算。
class Solution {
// Solution1:用栈存储,每当遇到运算符时,就从栈中弹出两个数进行计算后存入
// Note:栈中只保存操作数,不保存运算符
public int evalRPN(String[] tokens) {
ArrayDeque<Integer> deque = new ArrayDeque<>();
for (String token : tokens) {
switch(token) {
case "+":
case "-":
case "*":
case "/":
int num1 = deque.pop();
int num2 = deque.pop();
deque.push(caculate(num1, num2, token));
break;
default: // 不是运算符,则入栈
deque.push(Integer.parseInt(token));
}
}
return deque.poll(); // 最后栈中只剩下最终结果
}
public int caculate(int a, int b, String operator) {
switch(operator) {
case "+":
return a + b;
case "-":
return b - a;
case "*":
return b * a;
case "/":
return b / a;
default:
return 0;
}
}
}
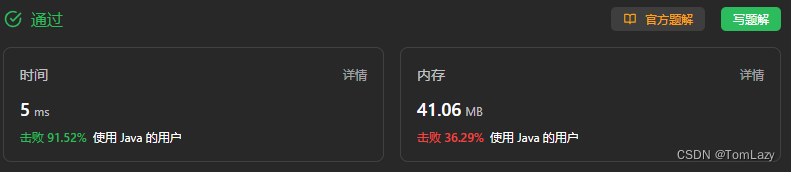
2. 剑指 Offer II 037. 小行星碰撞 – P96
给定一个整数数组
asteroids,表示在同一行的小行星。
对于数组中的每一个元素,其绝对值表示小行星的大小,正负表示小行星的移动方向(正表示向右移动,负表示向左移动)。每一颗小行星以相同的速度移动。
找出碰撞后剩下的所有小行星。碰撞规则:两个行星相互碰撞,较小的行星会爆炸。如果两颗行星大小相同,则两颗行星都会爆炸。两颗移动方向相同的行星,永远不会发生碰撞。
2.1 分类讨论 + 栈 – O(n)(⭐)
时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( n ) O(n) O(n)
class Solution {
public int[] asteroidCollision(int[] asteroids) {
ArrayDeque<Integer> deque = new ArrayDeque<>();
for (int as : asteroids) {
// 1. 栈非空,相向碰撞,保留大值
while (!deque.isEmpty() && deque.peek() > 0 && deque.peek() < -as) {
deque.pop();
}
// 2. 栈非空,相向碰撞,同归于尽
if (!deque.isEmpty() && as < 0 && deque.peek() == -as) {
deque.pop();
}
// 3. 同向 | 栈为空 ,则入栈
else if (as > 0 || deque.isEmpty() || deque.peek() < 0) {
deque.push(as);
}
}
int[] res = new int[deque.size()];
for (int i = res.length-1; i >= 0; i--) {
res[i] = deque.pop();
}
return res;
}
}
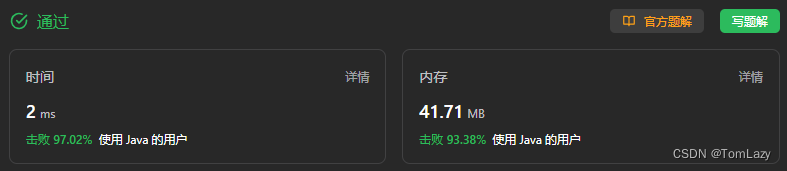
3. 剑指 Offer II 038. 每日温度 – P98
请根据每日 气温 列表
temperatures,重新生成一个列表,要求其对应位置的输出为:要想观测到更高的气温,至少需要等待的天数。如果气温在这之后都不会升高,请在该位置用0来代替。
3.1 单调栈 – O(n)(⭐)
时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( n ) O(n) O(n)
关于单调栈的更多内容可参考:【华为机考】专题突破 第一周:单调栈 739 、503 、901、84
……
该题解中的栈存储的是元素的 下标。
class Solution {
// Solution1:单调栈
public int[] dailyTemperatures(int[] temperatures) {
int[] res = new int[temperatures.length];
Stack<Integer> sk = new Stack<>();
for (int i = 0; i < temperatures.length; i++) {
// 如果栈非空,且当前气温大于栈顶气温,则计算等待天数,并弹出栈顶元素
while (!sk.empty() && temperatures[i] > temperatures[sk.peek()]) {
int index = sk.pop();
res[index] = i - index;
}
// 顺序添加每个元素,不存在更大气温的元素会被永远存在栈中
sk.push(i);
}
return res;
}
}
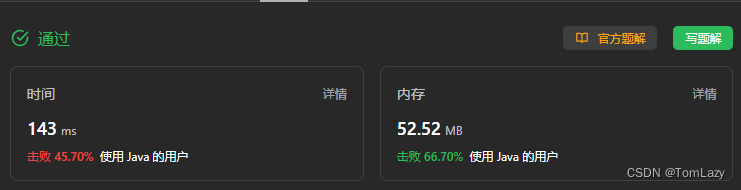
4. 剑指 Offer II 039. 直方图最大矩形面积 – P100
给定非负整数数组
heights,数组中的数字用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
4.1 单调栈 – O(n)(⭐)
时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( n ) O(n) O(n)
Key:每次计算的是某某高度下的矩形的最大面积。高为出栈元素高度,宽则为比该出栈元素小的两侧元素下标的差值。
class Solution {
// Solution1:单调递增栈,栈中存储元素下标
public int largestRectangleArea(int[] heights) {
Stack<Integer> sk = new Stack<>();
sk.push(-1); // 初始下标
int max = 0;
for (int i = 0; i < heights.length; i++) {
// 如果当前元素小于或等于栈顶元素,则让栈顶元素出栈,同时计算栈顶高度矩形的最大面积
while (sk.peek() != -1 && heights[sk.peek()] >= heights[i]) {
int h = heights[sk.pop()];
int w = i - sk.peek() - 1;
max = Math.max(max, h * w);
}
// 栈中元素始终保持单调递增
sk.push(i);
}
while (sk.peek() != -1) { // 计算栈中剩余元素高度矩形的最大面积
int h = heights[sk.pop()];
int w = heights.length - sk.peek() -1;
max = Math.max(max, h * w);
}
return max;
}
}
4.2 分治 – O(logn)
时间复杂度 O ( l o g n ) O(logn) O(logn),空间复杂度 O ( n ) O(n) O(n)
Key:将直方图的最大矩形分成了3种可能:1. 矩形通过最矮的柱子;2. 矩形的起始柱子和终止柱子都在最矮的柱子的左侧;3. 矩形的起始柱子和终止柱子都在最矮的柱子的右侧。
class Solution {
// Solution2:分治法
// 每次找最小的元素为中点,然后向左右两侧递归
public int largestRectangleArea(int[] heights) {
return helper(heights, 0, heights.length);
}
public int helper(int[] heights, int l, int r) {
if (l == r) return 0;
if (l+1 == r) return heights[l];
int minIndex = l;
for (int i = l+1; i < r; i++) {
minIndex = heights[i] < heights[minIndex] ? i : minIndex;
}
int max = (r - l) * heights[minIndex];
int left = helper(heights, l, minIndex);
int right = helper(heights, minIndex+1, r);
max = Math.max(max, left);
return Math.max(max, right);
}
}
5. 剑指 Offer II 040. 矩阵中的最大矩形 – P106
5.1 矩阵转直方图 + 单调栈 – O(mn)(⭐)
时间复杂度 O ( m n ) O(mn) O(mn),空间复杂度 O ( n ) O(n) O(n)
Key:要有抽象思维,将矩阵(01矩阵)抽象成直方图,求1所能构成矩形的最大面积,进而套用上一题的代码,求解直方图的最大面积。
class Solution {
// Solution1:将矩阵转化成直方图,求直方图的最大面积
public int maximalRectangle(String[] matrix) {
if (matrix.length == 0) return 0;
char[][] str = new char[matrix.length][];
for (int i = 0; i < matrix.length; i++) {
str[i] = matrix[i].toCharArray();
}
int[] heights = new int[str[0].length];
int res = 0;
for (char[] row : str) {
for (int i = 0; i < row.length; i++) {
if (row[i] == '0') {
heights[i] = 0;
} else {
heights[i]++;
}
}
res = Math.max(res, caculateArea(heights));
}
return res;
}
public int caculateArea(int[] heights) {
Stack<Integer> sk = new Stack<>();
sk.push(-1);
int max = 0;
for (int i = 0; i < heights.length; i++) {
while (sk.peek() != -1 && heights[sk.peek()] >= heights[i]) {
int h = heights[sk.pop()];
int w = i - sk.peek() - 1;
max = Math.max(max, h * w);
}
sk.push(i);
}
while (sk.peek() != -1) {
int h = heights[sk.pop()];
int w = heights.length - sk.peek() - 1;
max = Math.max(max, h * w);
}
return max;
}
}
6. 继续提升:加练题目
🎈 可参考:
- 栈 · SharingSource/LogicStack-LeetCode Wiki · GitHub
- 单调栈 · SharingSource/LogicStack-LeetCode Wiki · GitHub