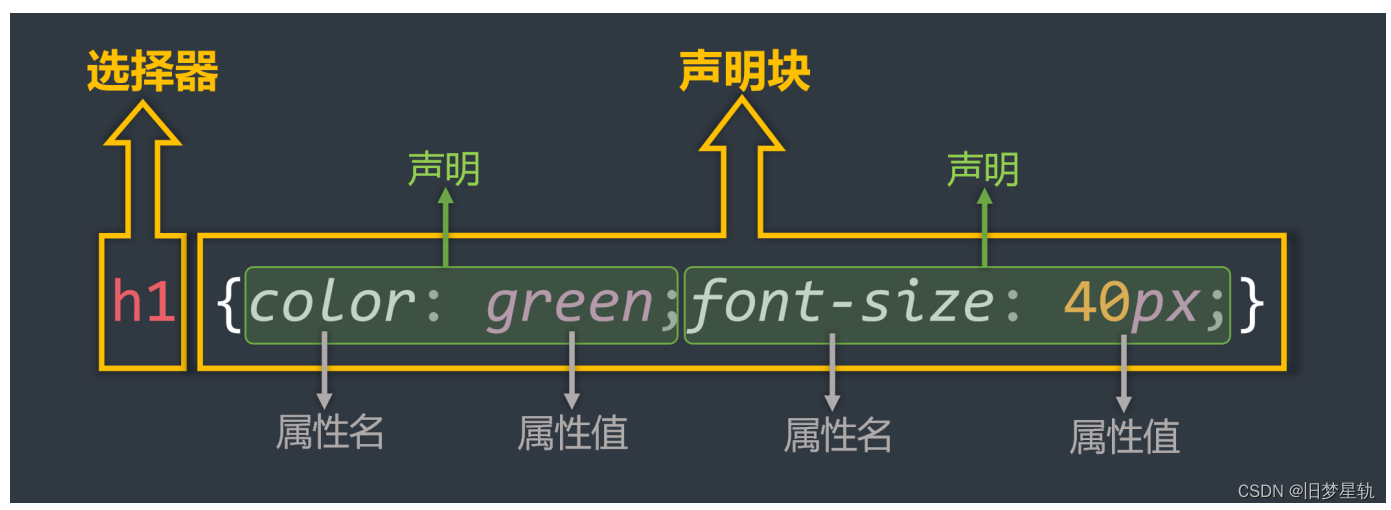
前缀树—Trie树,也叫作“单词查找树”、“字典树”
它属于多叉树结构,典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高
前缀树是一个由“路径”和“节点”组成多叉树结构。由根节点出发,按照存储字符串的每个字符,创建对应字符路径
存储结果如下

3个基本性质:
1.根节点不包含字符,除根节点外每一个节点都只包含一个字符(词组);
2.从根节点到某一节点,路径上经过的字符(词组)连接起来,为该节点对应的字符串;
3. 每个节点的所有子节点包含的字符都不相同。
基本操作有:查找、插入和删除, 删除操作不会删除节点
实现逻辑如下
前缀树节点定义
/// <summary>
/// 前缀树节点
/// </summary>
public class TrieNode
{
// 节点存的值
public string value = string.Empty;
// 经过该节点的次数
public int passCount = 0;
// 以此节点为终点的数量
public int endCount = 0;
// 子节点
public Dictionary<string, TrieNode> childMap = new Dictionary<string, TrieNode>();
}
前缀树实现
public class TrieTree
{
private TrieNode rootNode = null;
// 下面代码中处理的字符串是以下划线分割的字符串,如 A_B_C_D
public TrieTree()
{
rootNode = new TrieNode();
}
/// <summary>
/// 添加数据
/// </summary>
/// <param name="msg"></param>
public void Insert(string msg)
{
string[] arr = msg.Split('_');
int index = 0;
TrieNode node = rootNode;
while (index < arr.Length)
{
string key = arr[index];
TrieNode childNode = null;
// 子节点中不包含 key 则创建一个节点添加
if ( !node.childMap.TryGetValue(key, out childNode))
{
childNode = new TrieNode();
childNode.value = key;
childNode.passCount = 0;
childNode.endCount = 0;
node.childMap[key] = childNode;
}
// 经过该节点的次数 +1
childNode.passCount++;
if (index >= arr.Length - 1)
{
// 如果是结尾,则结尾数+1
childNode.endCount++;
}
// 令 node 等于 子节点
node = childNode;
++index;
}
}
/// <summary>
/// 搜索
/// </summary>
/// <param name="msg"></param>
/// <returns></returns>
public TrieNode Search(string msg)
{
if (string.IsNullOrEmpty(msg))
{
return rootNode;
}
string[] arr = msg.Split('_');
int index = 0;
TrieNode node = rootNode;
// 深度优先遍历
while (index < arr.Length)
{
string key = arr[index];
TrieNode childNode = null;
// 子节点中以 key 查找
if (!node.childMap.TryGetValue(key, out childNode))
{
break;
}
// 令 node 等于子节点
node = childNode;
++index;
}
return (index == arr.Length) ? node : null;
}
/// <summary>
/// 删除 msg
/// 前缀树不会删除节点,只是修改节点记录的 passCount、endCount
/// </summary>
/// <param name="msg"></param>
public void Remove(string msg)
{
string[] arr = msg.Split('_');
int index = 0;
TrieNode node = rootNode;
while (index < arr.Length)
{
string key = arr[index];
// 子节点中以 key 查找
if (!node.childMap.TryGetValue(key, out node))
{
break;
}
// 经过该节点的次数 -1
node.passCount--;
if (index == arr.Length - 1)
{
// 如果是结尾,则结尾数 -1
node.endCount--;
}
++index;
}
}
/// <summary>
/// 计算以 msg 为前缀的数量
/// </summary>
/// <param name="msg"></param>
/// <returns></returns>
public int PrefixCount(string msg)
{
TrieNode node = Search(msg);
if (null == node)
{
return 0;
}
return node.passCount;
}
/// <summary>
/// 计算存储的 msg 个数
/// </summary>
/// <param name="msg"></param>
/// <returns></returns>
public int EndCount(string msg)
{
TrieNode node = Search(msg);
if (null == node)
{
return 0;
}
return node.endCount;
}
/// <summary>
/// 打印所有前缀为 msg 的信息
/// </summary>
/// <param name="msg"></param>
public void PrefixTraverse(string msg)
{
// 先查找以 msg 为前缀的节点
TrieNode node = Search(msg);
if (null == node)
{
return;
}
List<string> list = new List<string>();
list.Add(msg);
// 遍历 所有子节点
foreach(var childNode in node.childMap.Values)
{
BackTracing(childNode, list);
}
}
/// <summary>
/// 回溯的查找所有子节点
/// </summary>
/// <param name="node"></param>
/// <param name="list"></param>
private void BackTracing(TrieNode node, List<string> list)
{
// 将节点的值添加到 list
list.Add(node.value);
// 如果节点是结尾则,将整个字符串打印出来
if (node.endCount > 0)
{
string msg = string.Empty;
foreach(var value in list)
{
msg += value;
}
Console.WriteLine(msg);
}
// 遍历所有子节点
foreach(var childNode in node.childMap.Values)
{
// 递归调用回溯算法
BackTracing(childNode, list);
}
// 将节点的值从 list 中删除 (此为回溯)
list.RemoveAt(list.Count - 1);
}
}
测试代码如下
public class TrieTreeTest
{
private static TrieTree tree = new TrieTree();
private static List<string> list = new List<string>() {
"A_B",
"A_B_C_D",
"A_B_C_D",
"A_B_C_D",
"A_B_C_F",
"A_B_E",
"A_B_E_D",
"B_C",
"B_C_D",
"B_C_E"
};
public static void Test()
{
foreach (var msg in list)
{
tree.Insert(msg);
}
TrieNode node = tree.Search("A");
foreach (var msg in list)
{
int preCount = tree.PrefixCount(msg);
int endCount = tree.EndCount(msg);
Console.WriteLine(msg + " pre:" + preCount + " end:" + endCount);
}
Console.WriteLine("=======================\n");
tree.PrefixTraverse("");
Console.WriteLine("=======================\n");
tree.Remove("A_B_C_D");
tree.Remove("A_B_C_D");
tree.Remove("B_C_D");
foreach (var msg in list)
{
int preCount = tree.PrefixCount(msg);
int endCount = tree.EndCount(msg);
Console.WriteLine(msg + " pre:" + preCount + " end:" + endCount);
}
Console.WriteLine("=======================\n");
tree.PrefixTraverse("");
Console.WriteLine("=======================\n");
}
前缀树是一种非常有用的字符串存储结构,它解决了像 HashMap 这种存储结构无法实现的问题——前缀统计,并且由于是复用节点,也很好的节约了存储空间