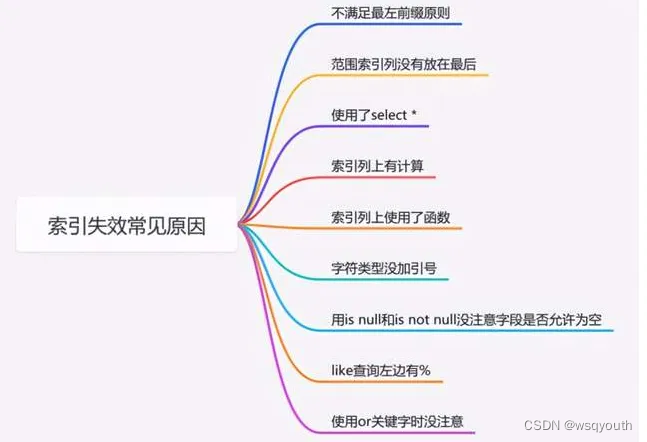
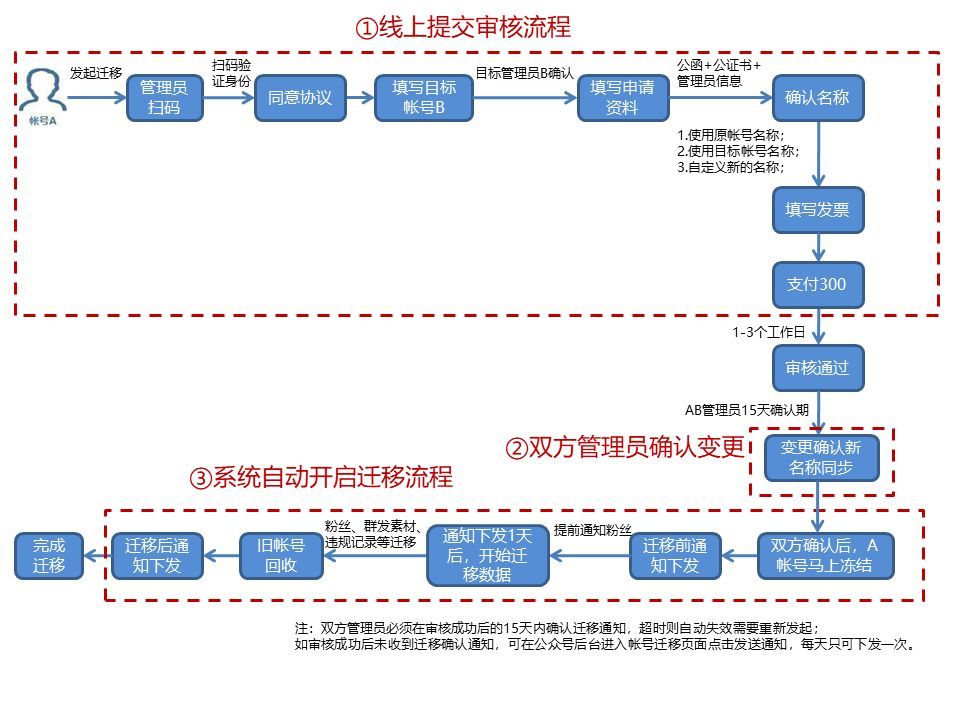
AC情况
| 赛中通过 | 赛后通过 | 暂未通过 | |
| A | √ | ||
| B | ○ | ||
| C | √ | ||
| D | - | ||
| E | √ | ||
| F | √ | ||
| G | ○ | ||
| H | - | ||
| I | ○ | ||
| J | - | ||
| K | √ |
整体体验
easy:AKF
mid:CEGI
hard:DHBJ
心得
整体感觉出的题比较传统,严格的卡精度/卡时间
题解
A. So I'll Max Out My Constructive Algorithm Skills(签到)
题意
n*n(n<=100)的矩阵放置了1-n*n的一个排列,每个位置一个数
在矩阵上走出一条路径,每次只能走相邻位置,且每个值都只能被访问一次,
对于这条路径序列a中的值,
计a[i]<a[i+1]为上升,a[i]>a[i+1]为下降,要求上升<=下降,输出任意可行a
题解
蛇形走位走出一条路径,如果正着合法就输出正序,
否则反序一定合法,序列反转后输出
代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
typedef unsigned ui;
//typedef __uint128_t L;
typedef unsigned long long L;
typedef unsigned long long ull;
const int N=65;
int t,n,a[N][N];
vector<int>ans;
bool ok(){
int up=n*n-1,cnt=0;
rep(i,1,up){
if(ans[i]<ans[i-1])cnt++;
else cnt--;
}
return cnt>=0;
}
void out(){
int up=n*n-1;
rep(i,0,up){
printf("%d%c",ans[i]," \n"[i==up]);
}
}
int main(){
sci(t);
while(t--){
sci(n);
ans.clear();
rep(i,1,n){
rep(j,1,n){
sci(a[i][j]);
if(i&1)ans.pb(a[i][j]);
}
if(i%2==0){
per(j,n,1)ans.pb(a[i][j]);
}
}
if(ok())out();
else{
reverse(ans.begin(),ans.end());
out();
}
}
return 0;
}K. Link-Cut Tree(并查集)
题意
n(n<=1e5)个点m(m<=1e5)条边的无向图,第i条边的权值是,
求最小权值的环,输出环上边的边号,不存在输出-1
题解
由于,所以前i条边全取了还没形成环再取第i+1条边,
如果第x条边(u,v)加入并查集时成环了,
那么在加入前,u和v在一棵树上,dfs一下之前的这棵树上u、v之间的链
所以一边维护并查集一边建树即可
代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
typedef unsigned ui;
//typedef __uint128_t L;
typedef unsigned long long L;
typedef unsigned long long ull;
const int N=1e5+10;
int t,n,m,a[N],b[N],par[N];
bool ok[N];
vector<P>e[N];
vector<int>ans;
int find(int x){
return par[x]==x?x:par[x]=find(par[x]);
}
void dfs(int u,int fa,int lf){
for(auto &x:e[u]){
int v=x.fi,id=x.se;
if(v==fa)continue;
dfs(v,u,lf);
ok[u]|=ok[v];
if(ok[u] && ok[v])ans.pb(id);
}
if(u==lf)ok[u]=1;
}
int main(){
sci(t);
while(t--){
sci(n),sci(m);
rep(i,1,n){
ok[i]=0;
e[i].clear();
par[i]=i;
}
rep(i,1,m){
sci(a[i]),sci(b[i]);
}
rep(i,1,m){
int u=a[i],v=b[i];
if(find(u)==find(v)){
dfs(u,0,v);
sort(ans.begin(),ans.end());
ans.pb(i);
break;
}
else{
par[find(v)]=find(u);
e[u].pb(P(v,i));
e[v].pb(P(u,i));
}
}
int sz=SZ(ans);
if(sz){
rep(i,0,sz-1){
printf("%d%c",ans[i]," \n"[i==sz-1]);
}
}
else{
puts("-1");
}
ans.clear();
}
return 0;
}F. Sandpile on Clique(优先队列)
题意
背景提到完全图的团,但是完全没有必要
n(n<=5e5)个数,第i个数ai(0<=ai<=1e9),
一次操作你可以选择一个大于等于n-1的数,令这个数减n-1,令其他n-1个数加1,
问所有数都小于n-1时的序列是什么样子的,
如果不管怎么操作都不能使所有数都小于n-1,输出Recurrent
题解
和最大的情况是n个数每个数都是n-2,如果n个数之和超过n*(n-2)显然是不行的,判掉
否则如果有解的话,大概可以证明操作数应该是一个和n量级差不多的数,
也就是每个数都操作一遍,这里取了2n,避免一些边角情况
操作可以等价视为令一个数减n,再令所有数+1,+1就可以通过cnt打全局标记了
每次堆顶找到最大数进行操作,
直到堆顶的数小于n-1后输出序列,或者总次数超过2n后陷入无限循环
代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
typedef unsigned ui;
//typedef __uint128_t L;
typedef unsigned long long L;
typedef unsigned long long ull;
const int N=5e5+10,Q=(1<<19)+5,M=320;
const long double PI=acos(-1.0);
int n;
ll sum,a[N];
priority_queue<P>q;
int main(){
sci(n);
rep(i,1,n){
scanf("%lld",&a[i]);
q.push(P(a[i],i));
sum+=a[i];
}
if(sum>1ll*n*(n-2)){
puts("Recurrent");
return 0;
}
int cnt=0;
while(cnt<=2*n){
P x=q.top();q.pop();
if(x.fi+cnt<n-1){
a[x.se]+=cnt;
while(!q.empty()){
x=q.top();q.pop();
a[x.se]+=cnt;
}
break;
}
else{
a[x.se]-=n;
q.push(P(a[x.se],x.se));
cnt++;
}
}
if(cnt>2*n){
puts("Recurrent");
}
else{
rep(i,1,n){
printf("%lld%c",a[i]," \n"[i==n]);
}
}
return 0;
}C. Laser Trap(计算几何 极角排序)
题意
二维平面上n(n<=1e6)个点,第i个点(xi,yi)(-1e9<=x,y<=1e9),保证不存在两点和(0,0)共线
任意两点之间都有一条连线,若干条连线将(0,0)围住在封闭图形里
求最少删掉多少个点,使得(0,0)能逃脱连线的围困,也即和无穷远是连通的
题解
考虑逃脱围困时剩下的点的情况,剩下的点一定在某个<180度的半平面内,
所以四象限极角排序后,枚举半平面一侧的点,双指针找到另一侧最远的点
遍历一圈更新答案,排序后二分也可以
Tip
被卡了若干发double的精度,所以不能用atan2,只能用long long的叉积
代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
typedef unsigned ui;
//typedef __uint128_t L;
typedef unsigned long long L;
typedef unsigned long long ull;
const int N=1e6+10,Q=(1<<19)+5,M=320;
const double PI=acos(-1.0);
int t,n;
struct Point{
ll x,y;
}e[N*2];
db det(Point a,Point b){
return a.x*b.y-a.y*b.x;
}
bool cmp(Point a,Point b){
if(!det(a,b))return a.x<b.x;
return det(a,b)>=0;
}
int f(Point a){
if(a.x>0 && a.y>=0)return 1;
if(a.x<=0 && a.y>0)return 2;
if(a.x<0 && a.y<=0)return 3;
if(a.x>=0 && a.y<0)return 4;
return 0;
}
bool cmp2(Point a,Point b){
if(f(a)!=f(b))return f(a)<f(b);
return cmp(a,b);
}
int main(){
sci(t);
while(t--){
sci(n);
rep(i,1,n){
scanf("%lld%lld",&e[i].x,&e[i].y);
}
sort(e+1,e+n+1,cmp2);
int m=2*n;
rep(i,n+1,m){
e[i]=e[i-n];
}
int j=1,ans=0;
rep(i,1,n){
j=max(j,i);
Point c;
c.x=-e[i].x;
c.y=-e[i].y;
while(j+1<=i+n-1 && det(c,e[j+1])<=0){
j++;
}
//printf("i:%d (%lld,%lld) fan:(%lld,%lld) j:%d\n",i,e[i].x,e[i].y,c.x,c.y,j);
ans=max(ans,j-i+1);
}
printf("%d\n",n-ans);
}
return 0;
}E. Pass the Ball!(FFT/根号分治+FFT)
题意
n(n<=1e5)个人,初始时第i个人有第i号球,
给定一个排列p,代表一轮操作后,第i个人会把当前手里的球传给pi
q(q<=1e5)次询问,每次给定一个k(k<=1e9),
询问k次操作后的值,其中b[i]为k次操作后第i个人手里拿的球的编号
题解
先考虑一下暴力怎么做,是对于每个长为sz的环,记p=k%sz,
遍历环上的每个点,执行以下操作,其中cyc是这个环的序列
for(int j=0;j<sz;++j){ ans+=1ll*cyc[j]*cyc[(j+p)%sz]; }
也就是环上i-j=p的(i,j)对会有贡献,所以可以FFT自卷积,
先翻转其中一个序列,令j=n-1-j,则p+n-1位置的值即为所求
再将另一个序列扩展为原来二倍,解决循环中i>j的问题
即ans=rev(a)*(a+a),rev为翻转,+为拼接,*为卷积
卷积后将相同长度的环合并在一起,暴力遍历每种长度的环,
由于环长不超过根号的只有根号种取值,超过根号的只有根号个环,复杂度O(nlogn+qsqrt(n))
Tip
①也可以直接根号分治,不超过根号的用暴力,超过根号的FFT后直接遍历每个环,就不用合并的过程了
②FFT内部也可以根号分治,不超过根号的用暴力背包,超过的再用FFT
③需要开long double,不然1e15会有double精度问题,任意模数NTT会很难写
代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
typedef unsigned ui;
//typedef __uint128_t L;
typedef unsigned long long L;
typedef unsigned long long ull;
const int N=1e5+10,Q=(1<<19)+5,M=320;
const long double PI=acos(-1.0);
int n,q,d[N],up[N],las[N],b,c,z;
bool vis[N];
vector<ll>cyc[N],add[N];
struct C{
long double r,i;
C(){}
C(long double a,long double b){r=a,i=b;}
C operator + (C x){return C(r+x.r,i+x.i);}
C operator - (C x){return C(r-x.r,i-x.i);}
C operator * (C x){return C(r*x.r-i*x.i,r*x.i+i*x.r);}
}w[Q],A[Q],B[Q];
int R[Q];
void FFT(C a[],int n){
for (int i=0;i<n;i++)
if (i<R[i])
swap(a[i],a[R[i]]);
for (int t=n>>1,d=1;d<n;d<<=1,t>>=1)
for (int i=0;i<n;i+=(d<<1))
for (int j=0;j<d;j++){
C tmp=w[t*j]*a[i+j+d];
a[i+j+d]=a[i+j]-tmp;
a[i+j]=a[i+j]+tmp;
}
}
void FFT_times(vector <ll> &a,vector <ll> &b,vector<ll>&c){
int n,d;
for (int i=0;i<a.size();i++)
A[i]=C(a[i],0);
for (int i=0;i<b.size();i++)
B[i]=C(b[i],0);
for (n=1,d=0;n<a.size()+b.size()-1;n<<=1,d++);
for (int i=0;i<n;i++){
R[i]=(R[i>>1]>>1)|((i&1)<<(d-1));
w[i]=C(cos(2*PI*i/n),sin(2*PI*i/n));
}
for (int i=a.size();i<n;i++)
A[i]=C(0,0);
for (int i=b.size();i<n;i++)
B[i]=C(0,0);
FFT(A,n),FFT(B,n);
for (int i=0;i<n;i++)
A[i]=A[i]*B[i],w[i].i*=-1.0;
FFT(A,n);
int up=a.size()+b.size()-1;
c.resize(up);
for (int i=0;i<up;i++)
c[i]=((ll)(A[i].r/n+0.5));
}
int main(){
sci(n),sci(q);
rep(i,1,n){
sci(d[i]);
}
rep(i,1,n){
if(vis[i])continue;
++c;
for(int j=i;!vis[j];j=d[j]){
cyc[c].pb(j);
vis[j]=1;
}
up[c]=SZ(cyc[c]);
vector<ll>tmp=cyc[c];
tmp.insert(tmp.end(),cyc[c].begin(),cyc[c].end());
reverse(cyc[c].begin(),cyc[c].end());
FFT_times(cyc[c],tmp,add[c]);
}
rep(i,1,c){
int sz=up[i];
if(!las[sz]){
add[++b]=add[i];
up[b]=up[i];
las[sz]=b;
}
else{
rep(j,sz-1,2*sz-2){
add[las[sz]][j]+=add[i][j];
}
}
}
while(q--){
sci(z);
ll ans=0;
rep(i,1,b){
int sz=up[i],p=z%sz;
ans+=add[i][sz-1+p];
// rep(j,0,sz-1){
// ans+=1ll*cyc[i][j]*cyc[i][(j+p)%sz];
// }
}
printf("%lld\n",ans);
}
return 0;
}G. Cyclic Buffer(dp+树状数组/set)
题意
循环书架里有n(n<=1e6)本书,只有位置处于1-k的这k本是可以看的,
一次操作,可以将书架里的所有书循环右移一次,或者循环左移一次,
为了增序看完1-n这n本书,求至少操作多少次
题解
如果第一本书已经在[1,k]里了,那么无需操作,只需要找到下一个需要操作的书即可
如果没在[1,k],只需将第一本书操作到1的位置或者k的位置,
再根据后面的书需要操作的情况挪动,
所以,dp[i][2]表示第i本书位于位置1/位置k时,后面的书都能读完的最小操作次数
nex[i][2]表示第i本书位于位置1/位置k时,下一个操作的书的编号(也即,>i的最小的不在[1,k]的书的编号是多少)
求nex[i][2]可以循环扫一遍数组,set维护当前不在[1,k]的数的值,
这样每次就是在set上二分大于i的最小的值,
但是,set常数太大了没卡过去(不然六题了)
所以用树状数组,每插入一个值时,在这个值上加1,
需要找x的后继的时候,先查一下树状数组<=x的值的个数,记为v,
然后树状数组上二分第k+1大,兼容不存在可以在n+1的位置先加个1
代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
typedef unsigned ui;
//typedef __uint128_t L;
typedef unsigned long long L;
typedef unsigned long long ull;
const int N=1e6+10,INF=0x3f3f3f3f;
const double PI=acos(-1.0);
ll dp[N][2];
int t,n,k,a[N],pos[N],nex[N][2];//dp[i][2]表示第i个位于最左最右的最小代价
struct BitPre{ // 求前缀和(可改为max等)
int n,tr[N];
void init(int _n){
n=_n;
memset(tr,0,(n+1)*sizeof(*tr));
}
void add(int x,int v){
for(int i=x;i<=n;i+=i&-i)
tr[i]+=v;
}
int ask(int x){
int ans=0;
for(int i=x;i;i-=i&-i)
ans+=tr[i];
return ans;
}
// 树状数组求从小到大第k个, 1<=k<=sum(n), 1<=x<=n
int kth(int k){
int x=0;
for(int i=1<<std::__lg(n);i;i>>=1){
if(x+i<=n && k>tr[x+i]){
x+=i;
k-=tr[x];
}
}
return x+1;
}
}tr;
//把x挪到p的最小代价
int cal(int x,int p){
int v=abs(x-p);
return min(v,n-v);
}
int f(int x){
return tr.kth(tr.ask(x)+1);
}
ll sol(){
if(n==k)return 0;
tr.init(n+1);
tr.add(n+1,1);
rep(i,k+1,n){
tr.add(a[i],1);
}
nex[a[1]][0]=f(a[1]);
nex[a[k]][1]=f(a[k]);
int st=tr.kth(1);
rep(i,2,n){
int p=i-1+k;if(p>n)p-=n;
tr.add(a[p],-1);
tr.add(a[i-1],1);
nex[a[i]][0]=f(a[i]);
nex[a[p]][1]=f(a[p]);
}
per(v,n,1){
rep(p,0,1){
int nv=nex[v][p];
if(nv>n){
dp[v][p]=0;
continue;
}
int now=(p==0)?1:k,np=pos[nv]-pos[v];
if(np<0)np+=n;
np+=now;
if(np>n)np-=n;
dp[v][p]=min(dp[nv][0]+cal(np,1),dp[nv][1]+cal(np,k));
}
}
return min(dp[st][0]+cal(pos[st],1),dp[st][1]+cal(pos[st],k));
}
int main(){
sci(t);
while(t--){
sci(n);sci(k);
//read(n);read(k);
for(int i=1;i<=n;++i){
dp[i][0]=dp[i][1]=-1;
nex[i][0]=nex[i][1]=n+1;
sci(a[i]);
//read(a[i]);
pos[a[i]]=i;
}
printf("%lld\n",sol());
}
return 0;
}I. LCS Spanning Tree(后缀数组)
题意
n(n<=2e6)个仅有小写字母构成的串,串长总和不超过2e6
第i个串代表点i,连接点i和点j的代价是LCS(s[i],s[j])(即第i个串的最长公共子串的长度)
求n个点的最大生成树的代价
题解
先将n个串用#连接之后得到新串,建新串的后缀数组,
两个串的LCS(最长公共子串)也就是两个后缀的LCP(最长公共前缀)
先跑板子求sa、rank、height,
然后只需按height从大到小维护并查集,建最大生成树即可
这样做为什么是对的呢
首先证连通,n个串所在的后缀位于新串的不同位置,
合并相邻项,一定可以将n个点合并连通
然后证最大,反证法,假设最优最大生成树上存在交叉边1-2-3,2连3,1连3
则根据LCP=min(RMQ(height))的性质,1连2比1连3更优,所以只需要连相邻边
Tip
1. 补了#号之后,height可能越过#号得到一个较大但是非法的值,所以需要结合串长得到真实的height后,再重新按height排序,这是本题唯一的坑点
2. 整理了一个SAIS的板子跑了2604ms,倍增5s题跑了4741ms可还行
SAIS代码
#include<bits/stdc++.h>
//#include<iostream>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
typedef unsigned ui;
typedef long long ll;
const int N=4e6+10;
int par[N],sz[N],ed[N];
bool used[N];
int find(int x){
return par[x]==x?x:par[x]=find(par[x]);
}
struct SuffixArray{
char ss[N],tt[N];
int to[N];
P id[N];
int n,sa[N], rk[N], ht[N], s[N<<1], t[N<<1], p[N], cnt[N], cur[N];
#define pushS(x) sa[cur[s[x]]--] = x
#define pushL(x) sa[cur[s[x]]++] = x
#define inducedSort(v) \
fill_n(sa, n, -1); fill_n(cnt, m, 0); \
for (int i = 0; i < n; i++) cnt[s[i]]++; \
for (int i = 1; i < m; i++) cnt[i] += cnt[i-1]; \
for (int i = 0; i < m; i++) cur[i] = cnt[i]-1; \
for (int i = n1-1; ~i; i--) pushS(v[i]); \
for (int i = 1; i < m; i++) cur[i] = cnt[i-1]; \
for (int i = 0; i < n; i++) if (sa[i] > 0 && t[sa[i]-1]) pushL(sa[i]-1); \
for (int i = 0; i < m; i++) cur[i] = cnt[i]-1; \
for (int i = n-1; ~i; i--) if (sa[i] > 0 && !t[sa[i]-1]) pushS(sa[i]-1);
void sais(int n, int m, int *s, int *t, int *p) {
int n1 = t[n-1] = 0, ch = rk[0] = -1, *s1 = s+n;
for (int i = n-2; ~i; i--) t[i] = s[i] == s[i+1] ? t[i+1] : s[i] > s[i+1];
for (int i = 1; i < n; i++) rk[i] = t[i-1] && !t[i] ? (p[n1] = i, n1++) : -1;
inducedSort(p);
for (int i = 0, x, y; i < n; i++) if (~(x = rk[sa[i]])) {
if (ch < 1 || p[x+1] - p[x] != p[y+1] - p[y]) ch++;
else for (int j = p[x], k = p[y]; j <= p[x+1]; j++, k++)
if ((s[j]<<1|t[j]) != (s[k]<<1|t[k])) {ch++; break;}
s1[y = x] = ch;
}
if (ch+1 < n1) sais(n1, ch+1, s1, t+n, p+n1);
else for (int i = 0; i < n1; i++) sa[s1[i]] = i;
for (int i = 0; i < n1; i++) s1[i] = p[sa[i]];
inducedSort(s1);
}
template<typename T>
int mapCharToInt(int n, const T *str) {
int m = *max_element(str, str+n);
fill_n(rk, m+1, 0);
for (int i = 0; i < n; i++) rk[str[i]] = 1;
for (int i = 0; i < m; i++) rk[i+1] += rk[i];
for (int i = 0; i < n; i++) s[i] = rk[str[i]] - 1;
return rk[m];
}
// Ensure that str[n] is the unique lexicographically smallest character in str.
template<typename T>
void suffixArray(int n, const T *str) {
//s[n++]='a'-1;
int m = mapCharToInt(++n, str);
sais(n, m, s, t, p);
for (int i = 0; i < n; i++) rk[sa[i]] = i;
for (int i = 0, h = ht[0] = 0; i < n-1; i++) {
int j = sa[rk[i]-1];
while (i+h < n && j+h < n && s[i+h] == s[j+h]) h++;
if (ht[rk[i]] = h) h--;
}
}
inline void PR(){
string p(ss);
for(int i=0;i<n;++i)//i∈[0,n) rank[i]∈[1,n]
printf("Rank[%d]:%d\n",i,rk[i]);
for(int i=0;i<=n;++i){//i∈[1,n] sa[i]∈[0,n)
printf("sa[%d]:%d ",i,sa[i]);
cout<<p.substr(sa[i])<<endl;
}
for(int i=1;i<=n;++i)//i∈[1,n] ht[1]=0
printf("ht[%d]:%d\n",i,ht[i]);
}
ll solve(){
int m;
sci(m);
rep(i,1,m){
par[i]=i;
scanf("%s",tt);
sz[i]=strlen(tt);
int &x=sz[i];
rep(j,0,x-1){
ss[n]=tt[j];
to[n++]=i;
}
ed[i]=n-1;
ss[n++]='#';
}
suffixArray(n, ss);
//PR();
rep(i,1,n){
id[i]=P(ht[i],i);
int p=id[i].second,x=sa[p],y=sa[p-1];
int px=to[x],py=to[y],v=id[i].first;
if(ss[x]=='#' || ss[y]=='#')continue;
if(px==0 || py==0)continue;
int ux=ed[px]-x+1,uy=ed[py]-y+1;
id[i].first=min(id[i].first,ux);
id[i].first=min(id[i].first,uy);
//printf("i1:%d p:%d x:%d y:%d px:%d py:%d v:%d w:%d\n",i,p,x,y,px,py,v,w);
}
sort(id+1,id+n+1,greater<P>());
ll ans=0;
int cnt=0;
rep(i,1,n){
int p=id[i].second,x=sa[p],y=sa[p-1];
int px=to[x],py=to[y],v=id[i].first;
if(ss[x]=='#' || ss[y]=='#')continue;
if(px==0 || py==0)continue;
if(px==py)continue;
int pu=find(px),pv=find(py);
if(pv==pu)continue;
//printf("i2:%d p:%d x:%d y:%d px:%d py:%d v:%d\n",i,p,x,y,px,py,v);
par[pv]=pu;
cnt++;
ans+=v;
}
//printf("cnt:%d\n",cnt);
assert(cnt==m-1);
return ans;
}
}sa;
int main(){
printf("%lld\n",sa.solve());
return 0;
}
/*
7
jia
ran
jin
tian
chi
shen
me
2-4 ans=2
3-6
6-2
3-1
1-5
6-7
*/倍增代码
#include<bits/stdc++.h>
//#include<iostream>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
typedef unsigned ui;
typedef long long ll;
const int N=4e6+10;
int par[N],sz[N],ed[N];
bool used[N];
int find(int x){
return par[x]==x?x:par[x]=find(par[x]);
}
struct SuffixArray{
typedef long long ll;
static const int maxn=4e6+10;
char s[maxn],t[N];
int cnt[maxn],mx,n,rk[maxn],sa[maxn],tmp[maxn],ht[maxn],to[maxn];
P id[maxn];
inline void base_sort(){
memset(cnt,0,sizeof(*cnt)*(mx+1));
for(int i=1;i<=n;++i)++cnt[rk[i]];
for(int i=1;i<=mx;++i)cnt[i]+=cnt[i-1];
for(int i=n;i;--i)sa[cnt[rk[tmp[i]]]--]=tmp[i]; //--主要用于解决值相同的情形
}
inline void suffix_sort(){
mx=0;
for(int i=1;i<=n;++i)mx=max(mx,rk[i]=s[i]),tmp[i]=i;
base_sort();
for(int len=1,dif=0;dif<n;len<<=1,mx=dif){
int p=0;
for(int i=n-len+1;i<=n;++i)tmp[++p]=i;
for(int i=1;i<=n;++i)
if(sa[i]>len)
tmp[++p]=sa[i]-len;
base_sort();
swap(rk,tmp);
rk[sa[1]]=dif=1;
for(int i=2;i<=n;++i){
if(tmp[sa[i-1]]!=tmp[sa[i]]||tmp[sa[i-1]+len]!=tmp[sa[i]+len])++dif;
rk[sa[i]]=dif;
}
}
}
inline void calc_ht(){
for(int i=1,h=0;i<=n;++i){
if(h)--h;
int j=sa[rk[i]-1];
while(s[i+h]==s[j+h])++h;
ht[rk[i]]=h;
}
}
//rk[i]: 下标位置在i的后缀的排名
//sa[i]: 后缀排名第i的下标位置
//ht[i]: 排名第i和排名第i-1的LCP长度
//rk和sa互为反函数,rk、sa、ht下标、值均为[1,n]
inline void PR(){
string p(s+1);
for(int i=1;i<=n;++i)
printf("Rank[%d]:%d\n",i,rk[i]);
for(int i=1;i<=n;++i){
printf("sa[%d]:%d ",i,sa[i]);
cout<<p.substr(sa[i]-1)<<endl;
}
for(int i=1;i<=n;++i)
printf("ht[%d]:%d\n",i,ht[i]);
}
ll solve(){
int m;
sci(m);
rep(i,1,m){
par[i]=i;
scanf("%s",t);
sz[i]=strlen(t);
int &x=sz[i];
rep(j,0,x-1){
s[++n]=t[j];
to[n]=i;
}
ed[i]=n;
s[++n]='#';
}
suffix_sort();
calc_ht();
rep(i,1,n){
id[i]=P(ht[i],i);
int p=id[i].second,x=sa[p],y=sa[p-1];
if(x<1 || y<1 || s[x]=='#' || s[y]=='#')continue;
int px=to[x],py=to[y],v=id[i].first;
int ux=ed[px]-x+1,uy=ed[py]-y+1;
id[i].first=min(id[i].first,ux);
id[i].first=min(id[i].first,uy);
//printf("i1:%d p:%d x:%d y:%d px:%d py:%d v:%d w:%d\n",i,p,x,y,px,py,v,w);
}
sort(id+1,id+n+1,greater<P>());
ll ans=0;
int cnt=0;
rep(i,1,n){
int p=id[i].second,v=id[i].first,x=sa[p],y=sa[p-1];
if(x<1 || y<1 || s[x]=='#' || s[y]=='#')continue;
int px=to[x],py=to[y];
if(px==py)continue;
int pu=find(px),pv=find(py);
if(pv==pu)continue;
//printf("i2:%d p:%d x:%d y:%d px:%d py:%d v:%d\n",i,p,x,y,px,py,v);
par[pv]=pu;
cnt++;
ans+=v;
}
//printf("cnt:%d\n",cnt);
assert(cnt==m-1);
return ans;
}
}sa;
int main(){
printf("%lld\n",sa.solve());
return 0;
}
/*
7
jia
ran
jin
tian
chi
shen
me
2-4 ans=2
3-6
6-2
3-1
1-5
6-7
*/B. the Matching System(构造+dp)
题意
对于一个01串和一个仅由01*^构成的正则表达式,
从大到小遍历的正则表达式的匹配规则如下:

1. *,for i从L到0从大到小枚举,其中L是01串还没有被匹配的长度,每次枚举消耗1能量,
本次*匹配了01串的i个字符,然后去考虑正则表达式和01串剩下的部分,只要存在一个解,就立刻停下来,否则会尝试遍历完,如果遍历完也没有解,就会回溯到上一个*
2. 0,1,如果正则表达式没匹配完,但是01串已经到结尾了,就会回溯到上一个*,否则,消耗1能量去比较,如果相等则考虑剩下的部分,不等则回溯到上一个*
3. ^,如果正则表达式没匹配完,但是01串已经到结尾了,就会回溯到上一个*,否则,消耗1能量,通配当前字符,并比较剩下的部分
从小到大遍历的规则类似,只是*匹配的时候,会for i从0到L从小到大枚举,其余完全一样
现在要求消耗的能量最多,
给定长度n(n<=1e3),输出6行,
分别为从大到小正则串、与之对应的01串、消耗的最大能量
以及从小到大正则串、与之对应的01串、消耗的最大能量
题解
构造不出来,打表打的
先爆搜打表,打出长度为n时候消耗的最大能量的从大到小/从小到大都可能是哪些,找了找规律
都有若干个解,只保留了其中一个解
从大到小
正则表达式:特判n=1和n=2,n>=3时前面n-2个*,后面是0*
01串:前面一个0,后面n-1个1
次数:特判n=1和n=2,n>=3时,呈现出8、31、119、456,...的规律
BM跑了一下不是线性的,丢进OEIS里把式子搜出来一抄就过了
不依赖OEIS可能会是O(n^3)的dp暴力打表,或者优化一下到O(n^2)
从小到大
正则表达式:一半(向上取整)*一半(向下取整)^
01串:全0
次数:n=1时为1,n=2时+2,n=3时+2,n=4时+3,n=5时+3,以此类推
打表代码1(从大到小)
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<string,string> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
typedef unsigned ui;
typedef long long ll;
char w[5]="*^01";
char s[15],t[15],as[15],at[15];
vector<P>res;
int n,ans;
int solmx(){
int i=0,j=0;
vector<int>lef(n+1,0),pre(n+1,0),now(n+1,0);
int las=-1,cost=0;
for(int k=0;k<=n;++k){
lef[k]=-2;
pre[k]=las;
if(s[k]=='*')las=k;
}
while(i<n || j<n){
now[i]=j;
//printf("i:%d j:%d now:%d\n",i,j,now[i]);
if(i==n){
i=pre[i];
if(i==-1)break;
j=now[i];
continue;
}
if(s[i]=='*'){
if(lef[i]==-1){
lef[i]=-2;
i=pre[i];
if(i==-1)break;
j=now[i];
}
else{
if(lef[i]==-2)lef[i]=n-j;
j+=lef[i];lef[i]--;i++;
cost++;
}
}
else if(s[i]=='^'){
if(j==n){
i=pre[i];
if(i==-1)break;
j=now[i];
}
else{
i++;
j++;
cost++;
}
}
else{
if(j==n){
i=pre[i];
if(i==-1)break;
j=now[i];
continue;
}
cost++;
if(s[i]==t[j]){
i++;
j++;
}
else{
i=pre[i];
if(i==-1)break;
j=now[i];
}
}
}
if(!(i==n && j==n))cost=-1;
//printf("s:%s t:%s cost:%d\n",s,t,cost);
return cost;
}
void dfs2(int x){
if(x==n){
int v=solmx();
if(v>ans || v==ans){
if(v>ans)res.clear();
ans=v;
string bs(s),bt(t);
res.pb(P(s,t));
}
return;
}
rep(i,0,1){
t[x]=i+'0';
dfs2(x+1);
}
}
void sol(){
dfs2(0);
}
void dfs(int x){
if(x==n){
sol();
return;
}
rep(i,0,3){
s[x]=w[i];
dfs(x+1);
}
}
int main(){
for(n=3;n<=5;++n){
res.clear();ans=0;
dfs(0);
printf("n:%d ans:%d\n",n,ans);
for(auto &st:res){
printf("%s %s\n",st.first.c_str(),st.second.c_str());
}
}
return 0;
}
/*
n:2 ans:3
*^ 00
*^ 01
*^ 10
*^ 11
*0 00
*0 10
*1 01
*1 11
n:3 ans:8
*0* 011
*1* 100
n:4 ans:31
**0* 0111
**1* 1000
n:5 ans:119
***0* 01111
***1* 10000
n:6 ans:456
****0* 011111
****1* 100000
*/打表代码2(从小到大)
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<string,string> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
typedef unsigned ui;
typedef long long ll;
const int INF=0x3f3f3f3f;
char w[5]="*^01";
char s[15],t[15],as[15],at[15];
vector<P>res;
int n,ans;
int solmn(){
int i=0,j=0;
vector<int>lef(n+1,0),pre(n+1,0),now(n+1,0);
int las=-1,cost=0;
for(int k=0;k<=n;++k){
lef[k]=-2;
pre[k]=las;
if(s[k]=='*')las=k;
}
while(i<n || j<n){
now[i]=j;
//printf("i:%d j:%d now:%d\n",i,j,now[i]);
if(i==n){
i=pre[i];
if(i==-1)break;
j=now[i];
continue;
}
if(s[i]=='*'){
if(lef[i]==n-j+1){
lef[i]=-2;
i=pre[i];
if(i==-1)break;
j=now[i];
}
else{
if(lef[i]==-2)lef[i]=0;
j+=lef[i];lef[i]++;i++;
cost++;
}
}
else if(s[i]=='^'){
if(j==n){
i=pre[i];
if(i==-1)break;
j=now[i];
}
else{
i++;
j++;
cost++;
}
}
else{
if(j==n){
i=pre[i];
if(i==-1)break;
j=now[i];
continue;
}
cost++;
if(s[i]==t[j]){
i++;
j++;
}
else{
i=pre[i];
if(i==-1)break;
j=now[i];
}
}
}
if(!(i==n && j==n))cost=-1;
//printf("s:%s t:%s cost:%d\n",s,t,cost);
return cost;
}
void dfs2(int x){
if(x==n){
int v=solmn();
if(v>ans || v==ans){
if(v>ans)res.clear();
ans=v;
string bs(s),bt(t);
res.pb(P(s,t));
}
return;
}
rep(i,0,1){
t[x]=i+'0';
dfs2(x+1);
}
}
void sol(){
dfs2(0);
}
void dfs(int x){
if(x==n){
sol();
return;
}
rep(i,0,3){
s[x]=w[i];
dfs(x+1);
}
}
int main(){
for(n=1;n<=5;++n){
res.clear();ans=0;
dfs(0);
printf("n:%d ans:%d\n",n,ans);
for(auto &st:res){
printf("%s %s\n",st.first.c_str(),st.second.c_str());
}
}
return 0;
}打表代码3(从大到小的次数)
#include<bits/stdc++.h>
using namespace std;
typedef double db;
typedef pair<string,string> P;
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define rep(i,a,n) for (int i=a;i<=n;i++)
#define per(i,a,n) for (int i=n;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef vector<int> VI;
typedef pair<int,int> PII;
typedef long long ll;
const int N=15,mod=1e9+7;
typedef unsigned ui;
typedef long long ll;
int n,cnt;
char s[N],t[N];
bool ok;
void dfs(int x,int y){
//printf("x:%d y:%d\n",x,y);
if(x==n && y==n){
ok=1;
return;
}
if(x==n){
return;
}
if(ok)return;
if(s[x]=='*'){
int up=n-y;
for(int i=up;i>=0;--i){
if(ok)return;
cnt++;
dfs(x+1,y+i);
}
}
else{
if(y==n)return;
if(ok)return;
cnt++;
if(s[x]==t[y]){
dfs(x+1,y+1);
}
}
}
int main(){
for(n=3;n<=10;++n){
cnt=0;ok=0;
rep(i,0,n-1)s[i]=(i==n-2?'0':'*');
rep(i,0,n-1)t[i]=(i==0?'0':'1');
dfs(0,0);
printf("n:%d cnt:%d\n",n,cnt);
}
return 0;
}代码
#include<bits/stdc++.h>
using namespace std;
typedef double db;
typedef pair<string,string> P;
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef vector<int> VI;
typedef pair<int,int> PII;
typedef long long ll;
const int N=2e3+10,mod=1e9+7;
int n,c[N][N],inv[N];
int cal1(){
int v=5*(n-1)*(n-1)+5*(n-1)+2;
int w=1ll*inv[2]*inv[n]%mod*inv[n+1]%mod;
v=1ll*v*w%mod;
return 1ll*c[2*n-2][n-1]*v%mod;
}
int cal2(){
int v=n/2;
ll x=1ll*(v+4)*(v+1);
int xs=(n&1)?1:2;
x-=xs*(v+2);
return x%mod;
}
void sol1(){
if(n==1){
puts("*");
puts("0");
puts("1");
}
else if(n==2){
puts("*0");
puts("00");
puts("3");
}
else{
rep(i,1,n+1)putchar(i==n-1?'0':'*');puts("");
rep(i,1,n+1)putchar(i==1?'0':'1');puts("");
int m=2*n;
inv[0]=inv[1]=1;
rep(i,2,m+1){
inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
}
c[0][0]=1;
rep(i,1,m+1){
c[i][0]=c[i][i]=1;
rep(j,1,i){
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
//printf("i:%d j:%d c:%d\n",i,j,c[i][j]);
}
}
printf("%d\n",cal1());
}
}
void sol2(){
int l=n-n/2,r=n/2;
rep(i,1,l+1)putchar('*');
rep(i,1,r+1)putchar('^');
puts("");
rep(i,1,n+1)putchar('0');
puts("");
printf("%d\n",cal2());
}
int main(){
sci(n);
sol1();
sol2();
return 0;
}