动态规划:回文串问题
- 前言
- 回文串问题
- 1.回文子串(中等)
- 2.回文串分割IV(困难)
- 3.分割回文串II(困难)
- 4.最长回文子序列(中等)
- 5.让字符串成为回文串的最小插入次数(困难)
前言
动态规划往期文章:
- 动态规划入门:斐波那契数列模型以及多状态
- 动态规划:路径和子数组问题
- 动态规划:子序列问题
回文串问题
1.回文子串(中等)
链接:回文子串
-
题目描述

-
做题步骤
-
状态表示
依据前面的经验,我们尝试定义状态表示:
(1)以i位置为结尾的回文串个数。这个最好想到,但这道题很明显是不行的,因为只有以某一个位置为结尾的个数信息,无法推导出其它位置的状态表示。(不知道这些回文串的具体情况)
(2)以i位置为结尾的回文串是否为真。只要组成位置不同就视为不同回文子串,因此确定真假然后累加就可以。但这个表示还是不足,第一点是以i位置为结尾的回文串可能有很多;第二点就是无法推导转移方程。(原因和(1)差不多)
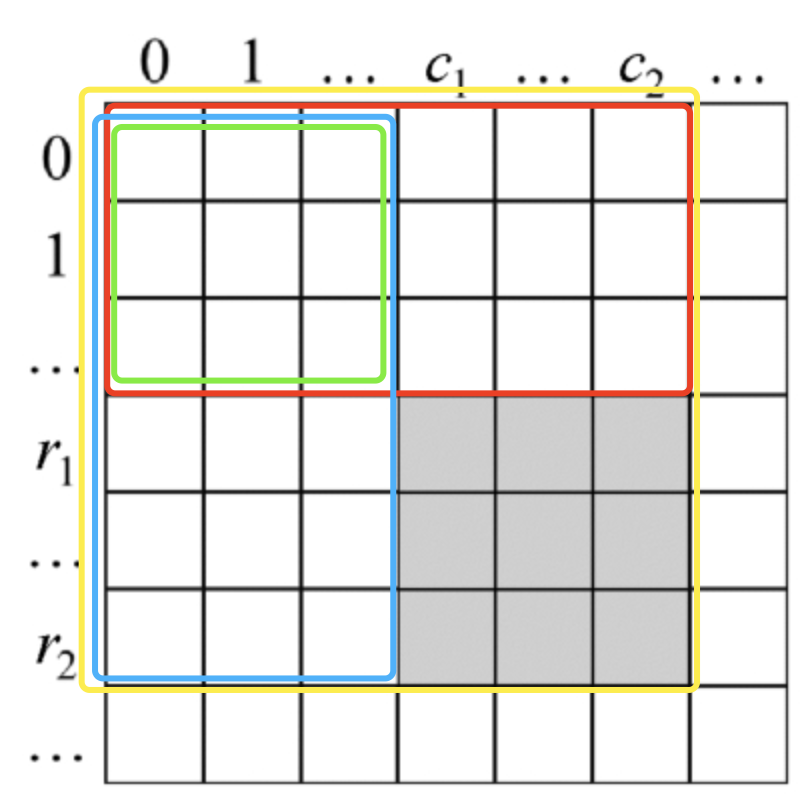
(3)上述表示不可行的主要原因就是没有利用回文串性质。对于[i , j]区间的字符串,如果s[i] == s[j]并且[i + 1, j - 1]区间为回文串,那[i, j]区间的字符串就是一个回文串。
故我们需要一个二维表dp[i][j]:[i, j]区间的子串是否为回文串。

-
状态转移方程
我们对[i, j]区间的子串进行分析:
(1)s[i] != s[j],为假,dp[i][j] = false。
(2)s[i] == s[j],这个分长度讨论:
①[i, j]区间长度为1,这个情况为真,dp[i][j] = true。
②[i, j]区间长度为2,这个情况也为真,dp[i][j] = true。
③[i, j]区间长度大于2(i + 1 < j),这个时候就要看[i - 1][j + 1]区间了,dp[i][j] = dp[i + 1][j - 1]。 -
初始化
开始全都初始化为false。 -
填表顺序
填当前位置可能需要左下角的状态,故填表顺序为行从下到上,每一行从左到右。 -
返回值
需要返回 dp 表中 true 的个数,用变量ret统计即可。
- 代码实现
class Solution {
public:
int countSubstrings(string s)
{
int n = s.size();
int ret = 0;
//dp[i][j]:字符串[i, j]的⼦串,是否是回⽂串。
vector<vector<bool>> dp(n, vector<bool>(n, false));
for (int i = n - 1; i >= 0; i--)
{
for (int j = i; j < n; j++)
{
//子串长度为三:i + 1 < j
if (s[j] == s[i])
dp[i][j] = (i + 1 < j ? dp[i + 1][j - 1] : true);
if (dp[i][j]) ret++; //累加个数
}
}
return ret;
//时间复杂度:O(N ^ 2)
//空间复杂度:O(N ^ 2)
}
};
2.回文串分割IV(困难)
链接:回文串分割IV
-
题目描述

-
做题步骤
- 算法思路
这个题目虽然标的是困难,但是有前面的基础其实还是比较容易的。
我们可以把问题拆分出来:
(1)先知道不同区间段的子串是否为回文串(第一题)
(2)枚举所有分成三段的情况,其中有一个为真即真,否则为假。
(把区间分成[0, i - 1],[i, j],[j + 1, n - 1]三段,枚举i与j即可)
- 代码实现
class Solution {
public:
bool checkPartitioning(string s) {
int n = s.size();
//dp[i][j]:字符串[i, j]的⼦串,是否是回⽂串。
vector<vector<bool>> dp(n, vector<bool>(n, false));
for (int i = n - 1; i >= 0; i--)
for (int j = i; j < n; j++)
if (s[j] == s[i])
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
//枚举判断能否分成三个
for(int i = 1; i < n - 1; i++)
for(int j = i; j < n - 1; j++)
if(dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1])
return true;
return false;
//时间复杂度:O(N ^ 2)
//空间复杂度:O(N ^ 2)
}
};
3.分割回文串II(困难)
链接:分割回文串II
-
题目描述

-
做题步骤
-
状态表示
我们对问题进行拆分:
(1)先知道不同区间段的子串是否为回文串(第一题)
(2)依据之前的做题经验,可以定义状态表示为dp[i]:[0, i]区间的字符串,使每个子串都是回文的最小切割次数。 -
状态转移方程
从[0, n - 1]枚举i:
(1)[0, i]直接就是回文串,需要的切割次数为0。
(2)[0, i]不是回文串:
枚举j,如果[j, i]为回文串,只需要让[0, j - 1]区间的字符串每个子串都是回文串,然后在j这个位置切一刀就行。即dp[i] = dp[j - 1] + 1。
但使[j, i]为回文串中满足条件的j可能有很多个,我们需要取其中的最小值。
例子:比如"aabb"这个例子:
①对于第一个b位置,前面aa是回文,需要切割的次数为0。要保持"aab"所有子串为回文,只能是b一个做回文,在这个位置切一刀,
dp[i] = 0 + 1。(0为保持"aa"所有子串为回文的最小切割次数)
②对于第二个b位置,要保持"aabb"所有子串回文,有两种选择。
i. 让"aa"所有子串保持回文,"bb"做回文,在这个位置切一刀,
即dp[i] = 0 + 1 = 1(0为保持"aa"所有子串为回文的最小切割次数)
ii. 让"aab"所有子串保持回文,b自己一个做回文,在这个位置切一刀,dp[i] = 1 + 1 = 2。(前面1为保持"aab"所有子串为回文的最小切割次数)。
取两种选择中次数最小的一方即可。 -
初始化
要多次取最小值,为避免默认0干扰结果,我们初始化为极大值。 -
填表顺序
填表顺序从左往右。 -
返回值
依据状态表示,返回值应该是dp[n - 1]。
- 代码实现
class Solution {
public:
int minCut(string s) {
int n = s.size();
//dp[i][j]:[i, j]区间是否为回文串
vector<vector<bool>> isPal(n, vector<bool>(n, false));
for (int i = n - 1; i >= 0; i--)
for (int j = i; j < n; j++)
if (s[j] == s[i])
isPal[i][j] = i + 1 < j ? isPal[i + 1][j - 1] : true;
vector<int> dp(n, INT_MAX);
//dp[i]:到这个位置保存回文需要切多少刀
for(int i = 0; i < n; i++)
{
if(isPal[0][i])
dp[i] = 0;
else
//j == 0,表示区间就是[0, i],进入这里[0, i]一定不是回文,可以不处理
for(int j = 1; j <= i; j++)
{
//[j, i]是回文
//这个位置要保证回文需要到j - 1位置保持回文并且在这个位置再切一刀
if(isPal[j][i])
dp[i] = min(dp[i], dp[j - 1] + 1);
}
}
return dp[n - 1];
}
};
4.最长回文子序列(中等)
链接:最长回文子序列
-
题目描述

-
做题步骤
-
状态表示
有第一题的经验,要充分利用回文串的性质,我们需要二维表。
我们定义状态表示dp[i][j]:[i, j]区间的中的最大回文子序列长度。 -
状态转移方程
我们对[i, j]区间分析:
(1)如果s[i] == s[j],那么我们只需要知道区间[i + 1, j - 1]的最大回文子序列长度,在这个长度的基础上加2即可,dp[i][j] = dp[i + 1][j - 1] + 2。
(把s[i]和s[j]接在前面和后面)
(2)如果s[i] != s[j],只有三种可能:
①s[i]可以接在[i + 1, j - 1]最长回文序列前面,dp[i][j] = dp[i][j - 1]。
②s[j]可以接在[i + 1, j - 1]最长回文序列后面,dp[i][j] = dp[i + 1][j]。
③s[i]或s[j]即不能接在[i + 1][j - 1]最长回文子序列前面,也不能接在后面,dp[i][j] = dp[i + 1][j - 1]。
其中③无论如何都是小于等于①②的情况的,填表时无需理会③。 -
初始化
(1)对于dp[i][i](一个字符做回文),需要初始化为1,这里就放在填表中处理了。
(2)其它位置初始化0即可。 -
填表顺序
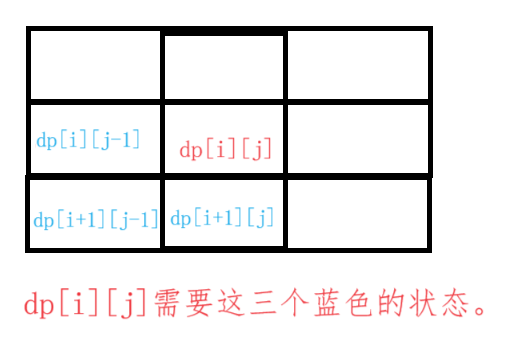
故填表顺序为行从下到上,每一行从左到右。 -
返回值
依据状态表示,返回值为dp[0][n - 1]。
- 代码实现
class Solution {
public:
int longestPalindromeSubseq(string s) {
int n = s.size();
//dp[i][j]表示[i,j]区间中的最大回文子序列
vector<vector<int>> dp(n, vector<int>(n));
for(int i = n - 1; i >= 0; i--)
{
dp[i][i] = 1;
for(int j = i + 1; j < n; j++)
{
//a(s[i]) [i + 1, j - 1] a(s[j]),[i + 1, j - 1]区间加2
//不是的话[i + 1, j],[i, j - 1]取最大
if(s[i] == s[j])
{
//dp[i][j] = (i + 1 < j) ? dp[i + 1][j - 1] + 2 : 2;
//刚好区间长度为2的时候[i + 1, j - 1]是无效区间
//这里无效区间刚好被初始化为0
dp[i][j] = dp[i + 1][j - 1] + 2;
}
else
{
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][n - 1];
}
};
5.让字符串成为回文串的最小插入次数(困难)
链接:让字符串成为回文串的最小插入次数
-
题目描述

-
做题步骤
-
状态表示
要充分利用回文串的性质,我们需要一个二维表。
我们定义状态表示为dp[i][j]:[i,j]区间修改成回文所需要的最小次数。 -
状态转移方程
对[i, j]区间进行分析:
(1)s[i] == s[j]。只需要让[i + 1][j - 1]修改成回文即可,我们需要[i + 1][j - 1]区间修改成回文所需要的最小次数,即dp[i][j] = dp[i + 1][j - 1]。
(2)s[i] != s[j],这个时候需要修改[i, j]为回文,有两种选择:
①在最前面插入一个s[j],这个时候只需要再修改[i][j - 1]区间为回文即可(比如bad,前面补充变成dbad,需要"ba"区间的最小修改次数)。即dp[i][j] = dp[i][j - 1] + 1。
②在最后面插入一个s[i],这个时候只需要再修改[i + 1][j]区间为回文即可(比如bad,后面补充变成badb,需要"ad"区间的最小修改次数)。即dp[i][j] = dp[i + 1][j] + 1。
取①②选择中修改次数最小的一方即可。 -
初始化
全都初始化为0即可。 -
填表顺序
和4题一样,填表顺序行从下到上,每一行从左到右。 -
返回值
依据状态表示,返回值为dp[0][n - 1]。
- 代码实现
class Solution {
public:
int minInsertions(string s) {
int n = s.size();
//dp[i][j]表示[i,j]区间修改成回文所需要的最小次数
vector<vector<int>> dp(n, vector<int>(n));
//最后一行可以不开,但那样初始化麻烦
for(int i = n - 1; i >= 0; i--)
{
for(int j = i + 1; j < n; j++)
{
//比如mbam,只需要知道"ba"区间的最小修改次数即可
if(s[i] == s[j])
{
//对于[i, j]长度2的情况,dp[i+1][j-1]刚好初始化为0
dp[i][j] = dp[i + 1][j - 1];
}
//比如bad,一种是前面补充->dbad,需要"ba"区间的最小修改次数
//一种是后面补充->badb,需要"ad"区间的最小修改次数
else
{
dp[i][j] = min(dp[i][j - 1], dp[i + 1][j]) + 1;
}
}
}
return dp[0][n - 1];
}
};