1. 概述
机器学习的定义是对于某类任务T和性能度量P,如果一个计算机程序在T上其性能P随着经验E而自我完善,那么我们就称这个系统从经验E中学习,机器学习是人工智能的一种方法,它通过在大量数据中学习隐藏的规则,模式和经验,对新的情况作出有效的决策。机器学习已经在多个行业广泛应用,在图像识别,语音识别,机器翻译,情感分析等多个领域取得不错的成果。
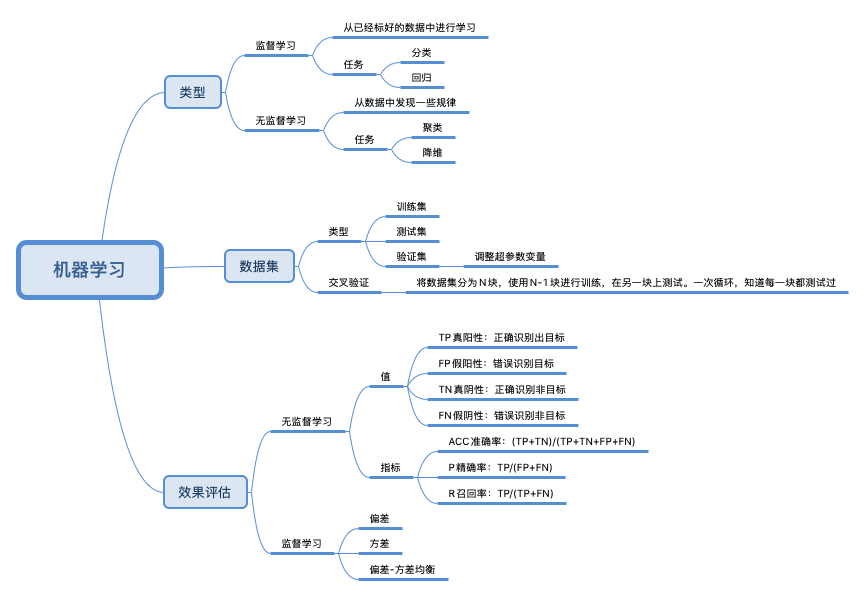
2. 分类
按学习的方式来划分,机器学习主要包括:
-
监督学习:输入数据带有标签。监督学习建立一个学习过程,将预测结果与 “训练数据”(即输入数据)的实际结果进行比较,不断的调整预测模型,直到模型的预测结果达到一个预期的准确率,比如分类和回归问题等。常用算法包括决策树、贝叶斯分类、最小二乘回归、逻辑回归、支持向量机、神经网络等。

-
非监督学习:输入数据没有标签,而是通过算法来推断数据的内在联系,比如聚类和关联规则学习等。常用算法包括独立成分分析、K-Means 和 Apriori 算法等。

-
半监督学习:输入数据部分被标识,部分没有被标识,这种学习模型可以用来进行预测,但是模型首先需要学习数据的内在结构以便合理的组织数据来进行预测。应用场景包括分类和回归,算法包括一些对常用监督式学习算法的延伸,这些算法首先试图对未标识数据进行建模,在此基础上再对标识的数据进行预测。如图论推理算法(Graph Inference)或者拉普拉斯支持向量机(Laplacian SVM)等。

-
强化学习:输入数据作为对模型的反馈,强调如何基于环境而行动,以取得最大化的预期利益。与监督式学习之间的区别在于,它并不需要出现正确的输入 / 输出对,也不需要精确校正次优化的行为。强化学习更加专注于在线规划,需要在探索(在未知的领域)和遵从(现有知识)之间找到平衡。 常见的应用场景包括动态系统以及机器人控制等。常见算法包括Q-Learning以及时间差学习(Temporal difference learning)

在企业数据应用的场景下, 人们最常用的可能就是监督式学习和非监督式学习的模型。 在图像识别等领域,由于存在大量的非标识的数据和少量的可标识数据, 目前半监督式学习是一个很热的话题。 而强化学习更多的应用在机器人控制及其他需要进行系统控制的领域。
3. sklearn库
在正式总结常用算法之前,需要先了解sklearn 库。
sklearn,全名 Scikit-learn,是 Python 中最常用的机器学习库之一,提供了各种常见的机器学习算法(分类、回归、聚类、降维等),并封装得非常好用,尤其适合入门和快速原型开发。
3.1 主要功能模块
- sklearn.linear_model :线性模型(如线性回归、逻辑回归)
- sklearn.naive_bayes :朴素贝叶斯分类器
- sklearn.tree :决策树、随机森林
- sklearn.svm :支持向量机
- sklearn.neighbors :KNN(近邻算法)
- sklearn.cluster :聚类算法(如 KMeans)
- sklearn.decomposition :降维(如 PCA)
- sklearn.preprocessing :数据预处理(标准化、归一化、编码等)
- sklearn.model_selection :数据划分、交叉验证、超参搜索
- sklearn.metrics :评估指标(准确率、F1 等)
3.2 典型的使用流程
以逻辑回归为例,展示 sklearn 的通用套路。
-
数据加载
-
数据划分
-
数据预处理
-
模型训练
-
模型预测
-
模型评估
-
模型保存 + 加载(可选)
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix
import joblib # 模型保存/加载
# 2. 加载数据
iris = load_iris()
X, y = iris.data, iris.target
print("特征维度:", X.shape)
print("类别:", np.unique(y))
# 3. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42, stratify=y)
# 4. 数据预处理(标准化)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 5. 模型训练
model = LogisticRegression(max_iter=1000)
model.fit(X_train, y_train)
# 6. 预测
y_pred = model.predict(X_test)
# 7. 模型评估
print("Confusion Matrix:")
print(confusion_matrix(y_test, y_pred))
print("\nClassification Report:")
print(classification_report(y_test, y_pred, target_names=iris.target_names))
# 8. 模型保存
joblib.dump(model, 'logistic_model.pkl')
joblib.dump(scaler, 'scaler.pkl')
# 9. 模型加载示例(可选)
# model = joblib.load('logistic_model.pkl')
# scaler = joblib.load('scaler.pkl')
注意:
X_train = scaler.fit_transform(X_train)
fit_transform 是 两步合一:
-
fit(X_train):计算训练集的均值和标准差
-
transform(X_train):用刚才计算出的均值和标准差来标准化训练集
X_test = scaler.transform(X_test)
这里只执行了 transform,意思是:
-
用 训练集的均值和标准差来标准化测试集
-
这一步不会重新计算均值和标准差
4. 常用的算法
机器学习算法主要可应用于三大场景:
- 分类,即机器被训练来完成对一组数据进行特定的分类。常见的算法有逻辑回归、朴素贝叶斯、决策树、随机森林、K 近邻、支持向量机,以及神经网络等等。
- 二分类:预测结果只有两个离散的值,如是否、1/0
- 多分类:预测结果是多个离散的值,如A/B/C
- 回归,即机器根据先前标记的数据来预测未来。预测结果是连续的值,如房价的预测、库存的预测。
- 聚类,无监督学习,将相似的样本归类在一起,如细分用户、新闻聚类。假设,你现在是一个客服系统负责人,为了减轻人工客服的压力,想把一部分常见的问题交给机器人来回复。解决这件事情的前提,就是我们要对用户咨询的商品问题先进行分组,找到用户最关心的那些问题。这种需要根据用户的特点或行为数据,对用户进行分组,让组内数据尽可能相似的的问题,就属于聚类问题,用一个词概括它的特点就是 “物以类聚”。常见的聚类算法有层次聚类、原型聚类(K-means)、密度聚类(DBSCAN)。其实,聚类算法的原理很简单,就是根据样本之间的距离把距离相近的聚在一起,在实际应用场景里,衡量样本之间距离关系的方法会更复杂,可能会用语义相似度、情感相似度等等。聚类分析较为重要的一个应用就是用户画像。
(1)逻辑回归
逻辑回归(Logistic Regression)是一种用于分类的机器学习算法,尽管它的名字中有“回归”二字,但它主要用于解决二分类问题。在逻辑回归中,目标变量(因变量)是离散的,通常是二元的(0和1),例如判断一封邮件是否是垃圾邮件(1表示垃圾邮件,0表示正常邮件)。和线性回归很像,但加了一个 Sigmoid 函数把结果压缩到 (0,1) 区间。
逻辑回归模型的形式可以表示为:
P
(
Y
=
1
∣
X
)
=
1
1
+
e
−
(
β
0
+
β
1
X
1
+
β
2
X
2
+
⋯
+
β
n
X
n
)
P(Y = 1 \mid X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_n X_n)}}
P(Y=1∣X)=1+e−(β0+β1X1+β2X2+⋯+βnXn)1
其中,P(Y=1∣X) 是在给定特征 X 的条件下,目标变量 Y 取值为1的概率。 β 0 β_0 β0 , β 1 β_1 β1, β 2 β_2 β2,…, β n β_n βn 是模型的参数, X 0 X_0 X0 , X 1 X_1 X1, X 2 X_2 X2,…, X n X_n Xn 是特征变量。这个模型的核心是一个逻辑函数,也称为 Sigmoid 函数,其形式为: σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1
Sigmoid 函数的输出范围在(0,1)之间,这使得它非常适合用来表示概率。
逻辑回归的损失函数通常是交叉熵损失函数(Cross - Entropy Loss)。对于二分类问题,交叉熵损失函数可以表示为:
L
(
β
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
log
(
y
^
(
i
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
y
^
(
i
)
)
]
L(\beta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(\hat{y}^{(i)}) + (1 - y^{(i)}) \log(1 - \hat{y}^{(i)}) \right]
L(β)=−m1i=1∑m[y(i)log(y^(i))+(1−y(i))log(1−y^(i))]
其中,m 是训练样本的数量, y ( i ) y^(i) y(i) 是第 i 个样本的真实标签, y ^ ( i ) \hat{y}^{(i)} y^(i) 是模型预测的样本为1的概率。这个损失函数衡量了模型预测的概率分布和真实标签的概率分布之间的差异。当模型预测的概率和真实标签越接近时,损失值越小。
逻辑回归模型的训练过程主要是通过优化算法来最小化损失函数,从而找到最优的模型参数 β。常用的优化算法有梯度下降法(Gradient Descent)。
(2)朴素贝叶斯
朴素贝叶斯(Naive Bayes)是一种基于贝叶斯定理的简单概率分类器,它假设特征之间相互独立。尽管这个假设在现实世界中往往不成立,但朴素贝叶斯分类器在许多实际应用中仍然表现出色,特别是在文本分类和垃圾邮件过滤等领域。
朴素贝叶斯分类器的核心是贝叶斯定理,其公式如下:
P
(
C
k
∣
X
)
=
P
(
X
∣
C
k
)
P
(
C
k
)
P
(
X
)
P(C_k \mid X) = \frac{P(X \mid C_k) P(C_k)}{P(X)}
P(Ck∣X)=P(X)P(X∣Ck)P(Ck)
其中:
P
(
C
k
∣
X
)
P(C_k \mid X)
P(Ck∣X) 是后验概率,即在给定特征 X 的条件下类别
C
k
C_k
Ck 的概率。
P
(
X
∣
C
k
)
P(X \mid C_k)
P(X∣Ck) 是似然函数,即在类别
C
k
C_k
Ck 的条件下观察到特征 X 的概率。
P
(
C
k
)
P(C_k)
P(Ck) 是类别
C
k
C_k
Ck 的先验概率。
P
(
X
)
P(X)
P(X) 是特征 X 的边缘概率,通常在计算中可以忽略,因为它对于所有类别都是相同的。
在计算
P
(
X
∣
C
k
)
P(X \mid C_k)
P(X∣Ck) 时,假设所有特征
x
1
,
x
2
,
.
.
,
x
n
x_1,x_2,..,x_n
x1,x2,..,xn 条件独立:
P
(
X
∣
C
k
)
=
P
(
x
1
,
x
2
,
…
,
x
n
∣
C
k
)
=
∏
i
=
1
n
P
(
x
i
∣
C
k
)
P(X \mid C_k) = P(x_1, x_2, \ldots, x_n \mid C_k) = \prod_{i=1}^{n} P(x_i \mid C_k)
P(X∣Ck)=P(x1,x2,…,xn∣Ck)=i=1∏nP(xi∣Ck)
这就是“朴素”的地方 —— 实际上大多数情况下特征并不独立,但这种简化让计算变得高效,而且在很多实际任务中效果 surprisingly 好。
常见的朴素贝叶斯模型:
-
高斯朴素贝叶斯(GaussianNB):用于连续数据,假设特征值服从高斯分布(正态分布)
-
多项式朴素贝叶斯(MultinomialNB):用于离散计数数据,常用于文本分类(如词频)
-
伯努利朴素贝叶斯(BernoulliNB):特征为二元(0或1),表示某个词是否出现,适合短文本分类
(3)决策树
决策树是一种树状模型,用于决策过程。它通过学习简单的决策规则从数据特征中推断出目标变量的值。其核心思想是通过一系列问题的判断,将数据逐步划分为不同的类别或预测目标值。它从根节点开始,通过选择最优的特征进行划分,逐步生成内部节点和叶子节点。最终,每个叶子节点代表一个类别或预测值。
例如,在一个二分类问题中,决策树可能会先根据一个特征(如年龄是否大于30)将数据分为两部分,然后在每个子部分继续根据其他特征进行划分,直到满足停止条件(如叶子节点的样本数量小于某个阈值或者树达到最大深度)。
分类树:用于分类任务,目标是将数据划分为不同的类别。
回归树:用于回归任务,目标是预测连续的数值。
决策树的结构: 由节点(Node)和分支(Branch)组成:
- 根节点(Root Node):决策树的起始点,包含整个数据集。
- 内部节点(Internal Node):表示一个特征或属性。
- 分支(Branch):表示从特征到两个子节点的决策路径。
- 叶节点(Leaf Node):表示最终的决策结果,即分类或回归的输出值。

构建过程:
构建决策树的关键在于如何选择最优的特征进行划分。常见的特征选择方法包括:
- 信息增益(Information Gain):基于信息熵的概念,选择使信息增益最大的特征。
- 增益率(Gain Ratio):对信息增益进行归一化,避免偏向于具有较多值的特征。
- 基尼不纯度(Gini Impurity):衡量数据的不纯度,选择使基尼不纯度最小的特征。
常见的决策树算法:
- ID3(Iterative Dichotomiser 3):使用信息增益作为特征选择标准。不能处理连续特征。
- C4.5:使用增益率作为特征选择标准。可以处理连续特征。
- CART(Classification and Regression Tree)可以用于分类和回归任务。使用基尼不纯度作为特征选择标准。
剪枝技术:
为了防止决策树过拟合,通常会采用剪枝技术,减少树的复杂度。常见的剪枝方法包括:
- 预剪枝(Pre-pruning):在树完全生长之前停止生长,例如限制树的深度或节点数量。
- 后剪枝(Post-pruning):先生成完整的树,然后通过剪掉一些分支来简化树结构。
优点:
- 决策树的结构直观,容易理解,可以清晰地展示决策过程。
- 既可以用于分类任务,也可以用于回归任务。
- 不需要特征缩放:对特征的数值范围不敏感。
缺点:
- 容易过拟合:在训练数据上表现很好,但在测试数据上可能泛化能力差。
- 对噪声数据敏感:噪声数据可能导致树结构发生较大变化。
- 计算复杂度高:尤其是当特征数量较多时,构建决策树的计算成本较高。

(4)随机森林
随机森林的核心是决策树。它通过构建多棵决策树来提高模型的性能。这些决策树是独立训练的,并且每棵树都是在不同的数据子集上训练的。
在训练随机森林中的每棵决策树时,会从原始训练数据集中使用有放回抽样方法抽取一个与原数据集大小相同的数据子集。这种方法称为Bootstrap抽样。例如,假设原始数据集有100个样本,对于随机森林中的第一棵决策树,会从这100个样本中有放回地抽取100个样本作为训练数据。由于是有放回抽样,所以这个子集中可能会有重复的样本,而有些样本可能一次也没有被抽到。这种抽样方式使得每棵决策树看到的数据是略有差异的,从而增加了模型的多样性。因为不同的数据子集可能会导致决策树在特征选择和划分方式上有所不同。
在构建每棵决策树的过程中,每次分裂节点时,并不是考虑所有特征。随机森林会从所有特征中随机选择一部分特征作为候选特征。例如,在一个有10个特征的数据集中,每次分裂节点时可能只随机选择3个特征来考虑。这样做的目的是进一步增加模型的随机性和多样性。如果每次都考虑所有特征,那么不同决策树之间的差异可能主要来源于数据抽样,而特征子集的选择可以让决策树在结构上更加不同,从而减少过拟合的风险。
对于分类任务,随机森林通过多数投票的方式来进行预测。例如,假设随机森林中有100棵决策树,对于一个测试样本,每棵决策树都会给出自己的预测类别。最后,随机森林会统计所有决策树预测结果中出现次数最多的类别作为最终的预测结果。
对于回归任务,随机森林则通过对所有决策树的预测结果取平均值来得到最终的预测值。如果每棵决策树对某个回归目标的预测值分别是1.2、1.5、1.3……,那么随机森林的预测值就是这些值的平均值。

优点:
- 抗过拟合能力强
由于随机森林通过Bootstrap抽样和特征子集选择等方式引入了随机性,使得每棵决策树的结构和预测结果都有所不同。这种多样性使得随机森林在面对复杂的、含有噪声的数据时,比单棵决策树更不容易过拟合。即使数据中存在一些异常值或者不重要的特征,随机森林也能够通过集成的方式降低它们对模型的影响。 - 适用范围广
随机森林既可以用于分类任务,也可以用于回归任务。对于分类任务,它可以处理多分类问题,并且对不平衡数据集也有一定的适应性。例如,在一个二分类问题中,正样本和负样本的比例可能相差很大,随机森林可以通过调整每棵决策树的训练数据等方式来缓解这种不平衡带来的影响。在回归任务中,它能够很好地拟合连续的数值目标变量。 - 特征重要性评估
随机森林可以提供特征重要性评分。在训练过程中,它会根据每个特征在所有决策树中的表现(如在分裂节点时对目标变量的贡献大小)来评估特征的重要性。这对于理解数据中的关键因素非常有帮助。例如,在一个医疗诊断问题中,通过随机森林可以发现哪些症状或检查指标对疾病的预测最为关键,从而为医学研究和临床诊断提供参考。 - 易于并行计算
随机森林中的每棵决策树是独立训练的,这意味着可以同时在多个处理器或者计算节点上并行训练这些决策树。这大大提高了模型的训练效率,尤其是在处理大规模数据集时。例如,如果有足够的计算资源,可以同时训练随机森林中的所有决策树,而不需要像一些顺序训练的模型那样等待前一步的完成。
缺点:
- 模型复杂度高
随机森林包含多棵决策树,每棵决策树本身又是一个复杂的结构。这使得随机森林模型的存储和计算成本相对较高。例如,对于一个包含几百棵决策树的随机森林模型,存储这些决策树结构需要占用较大的内存空间。在预测阶段,也需要对每棵决策树进行遍历,这会增加预测的计算时间。 - 可解释性较差
虽然随机森林可以提供特征重要性评分,但是相比于单棵决策树,它的整体可解释性要差一些。因为随机森林是由多棵决策树组合而成的,很难像单棵决策树那样直观地展示出模型的决策过程。例如,单棵决策树可以通过树状图清晰地展示出样本是如何根据特征逐步被划分到不同类别或预测值的,而随机森林的预测结果是基于多棵决策树的综合判断,很难用一个简单的逻辑来描述其决策路径。
(5)K 近邻
K 近邻算法(K-Nearest Neighbors,简称 KNN)是一种基本的分类与回归方法,通常用于分类问题。它的工作原理非常简单直观:给定一个训练数据集,对新的输入样本,算法会找到训练集中与其最接近的 K 个样本(即“邻居”),然后根据这些邻居的已知标签来预测新样本的标签。
主要步骤:
- 选择参数 K:K 是用户指定的一个正整数,表示邻居的数量。K 值的选择对算法的性能有很大影响。较小的 K 值意味着模型对数据中的噪声更敏感,而较大的 K 值则可能导致模型对数据的局部结构不够敏感。
- 距离度量:计算新样本与训练集中每个样本之间的距离。常用的距离度量方法包括欧氏距离、曼哈顿距离和闵可夫斯基距离等。
- 寻找最近的 K 个邻居:根据计算出的距离,选择距离最近的 K 个训练样本。
- 决策规则:
- 分类:在 K 个邻居中,选择出现次数最多的类别标签作为新样本的预测标签。
- 回归:计算 K 个邻居的目标值的平均值,作为新样本的预测值。
- 输出预测结果:根据决策规则,输出新样本的预测类别或连续值。

优点:
- 无需训练:KNN 是一种惰性学习算法,它不需要在训练阶段构建模型,所有的计算都在预测阶段进行。
- 适用于多分类问题:KNN 可以很容易地扩展到多分类问题。
- 可以用于非线性数据:KNN 不需要假设数据的分布,因此适用于非线性可分的数据。
缺点:
- 计算成本高:对于大数据集,计算每个新样本与所有训练样本的距离可能非常耗时。
- 存储成本高:KNN 需要存储整个训练数据集,这可能导致较高的存储需求。
- 对不平衡数据敏感:如果数据集中的类别分布不均匀,KNN 可能会偏向于多数类。
- 对噪声敏感:KNN 对数据中的噪声点较为敏感,这可能会影响分类的准确性。
(6)支持向量机
支持向量机(Support Vector Machine,简称SVM)是一种用于分类和回归分析的监督学习算法。它通过在特征空间中找到一个最优的超平面来区分不同类别的数据点。在二分类问题中,这个超平面能够最大化两个类别之间的间隔,从而实现良好的分类性能。
工作原理:
-
线性可分情况
- 超平面的定义
在二维空间中,超平面就是一条直线;在三维空间中,超平面是一个平面;在更高维空间中,超平面是一个线性子空间。假设我们有一个线性可分的数据集,每个数据点 x i x_i xi 都有一个类别标签 y i y_i yi ,其中 y i ∈ { − 1 , + 1 } y_i \in \{-1, +1\} yi∈{−1,+1}。超平面可以用方程 w ⋅ x + b = 0 w⋅x+b=0 w⋅x+b=0 表示,其中 w 是超平面的法向量,b 是截距。 - 间隔最大化
SVM的目标是找到一个超平面,使得两个类别之间的间隔最大。间隔可以用公式 2 ∣ w ∣ \frac{2}{|\mathbf{w}|} ∣w∣2 来表示。为了最大化间隔,我们需要最小化 ∥w∥。这可以通过求解以下优化问题来实现:
min w , b 1 2 ∥ w ∥ 2 \min_{\mathbf{w}, b} \frac{1}{2} \|\mathbf{w}\|^2 w,bmin21∥w∥2
y i ( w ⋅ x i + b ) ≥ 1 y_i(w \cdot x_i + b) \geq 1 yi(w⋅xi+b)≥1

- 超平面的定义
-
线性不可分情况
-
核函数的引入
在实际问题中,数据往往是线性不可分的。为了处理这种情况,SVM引入了核函数。核函数的作用是将数据映射到高维空间,在这个高维空间中数据可能变得线性可分。常见的核函数有:- 线性核: K ( x i , x j ) = x i ⋅ x j K(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i \cdot \mathbf{x}_j K(xi,xj)=xi⋅xj ,适用于线性可分的情况。
- 多项式核: K ( x i , x j ) = ( x i ⋅ x j + c ) d K(\mathbf{x}_i, \mathbf{x}_j) = (\mathbf{x}_i \cdot \mathbf{x}_j + c)^d K(xi,xj)=(xi⋅xj+c)d ,其中 c 和 d 是参数。可以处理非线性关系。
- 径向基函数(RBF)核: K ( x i , x j ) = exp ( − γ ∥ x i − x j ∥ 2 ) K(\mathbf{x}_i, \mathbf{x}_j) = \exp(-\gamma \|\mathbf{x}_i - \mathbf{x}_j\|^2) K(xi,xj)=exp(−γ∥xi−xj∥2) ,其中 γ 是参数。它是最常用的核函数之一,能够处理复杂的非线性关系。
- sigmoid核: K ( x i , x j ) = tanh ( α x i ⋅ x j + c ) K(\mathbf{x}_i, \mathbf{x}_j) = \tanh(\alpha \mathbf{x}_i \cdot \mathbf{x}_j + c) K(xi,xj)=tanh(αxi⋅xj+c) ,与神经网络中的激活函数类似,但使用较少。
-
优化问题的调整
- 当引入核函数后,SVM的优化问题变为:
min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 n ξ i \min_{\mathbf{w}, b, \xi} \frac{1}{2} \|\mathbf{w}\|^2 + C \sum_{i=1}^{n} \xi_i w,b,ξmin21∥w∥2+Ci=1∑nξi
y i ( w ⋅ x i + b ) ≥ 1 − ξ i , i = 1 , 2 , … , n ξ i ≥ 0 , i = 1 , 2 , … , n \begin{align*}\quad y_i(\mathbf{w} \cdot \mathbf{x}_i + b) \geq 1 - \xi_i, \quad i = 1, 2, \ldots, n & \quad \xi_i \geq 0, \quad i = 1, 2, \ldots, n\end{align*} yi(w⋅xi+b)≥1−ξi,i=1,2,…,nξi≥0,i=1,2,…,n
其中, ξ i \xi_i ξi 是松弛变量,用于允许一些数据点违反间隔约束。C 是正则化参数,用于控制间隔最大化和误分类之间的平衡。通过拉格朗日对偶方法,可以将优化问题转化为对偶问题,利用核函数来计算数据点之间的相似度。
- 当引入核函数后,SVM的优化问题变为:
-
多分类SVM:
原始的SVM是为二分类问题设计的。为了处理多分类问题,可以采用一些方法,如一对多(One - vs - All)、一对一(One - vs - One)等策略。在一对多方法中,对于每个类别,训练一个SVM模型,将该类别与其他所有类别区分开来。在一对一方法中,每两个类别之间训练一个SVM模型,最后通过投票等方式确定最终的类别。
优点:
- 分类性能好
SVM在许多实际问题中都表现出良好的分类性能,尤其是在高维空间中。它通过最大化间隔来寻找最优超平面,能够有效避免过拟合。 - 适用于小样本数据
SVM对小样本数据具有较好的适应性。它不需要大量的样本数据来训练模型,这在一些样本获取困难的领域(如生物医学领域)非常有优势。 - 核函数的灵活性
核函数的引入使得SVM能够处理非线性问题。通过选择合适的核函数,可以将数据映射到高维空间,从而找到更好的分类边界。
缺点:
- 计算复杂度高
SVM的训练过程涉及求解二次规划问题,计算复杂度较高。特别是当数据量较大时,训练时间可能会很长。 - 对核函数和参数选择敏感
SVM的性能很大程度上依赖于核函数的选择和参数的调整。不同的核函数和参数设置可能会导致不同的分类结果。在实际应用中,需要通过交叉验证等方法来选择合适的核函数和参数,这增加了模型的调试难度。 - 不适用于大规模数据集
由于计算复杂度的限制,SVM在处理大规模数据集时可能会遇到困难。相比之下,一些基于深度学习的算法在大规模数据集上可能具有更好的性能。


















