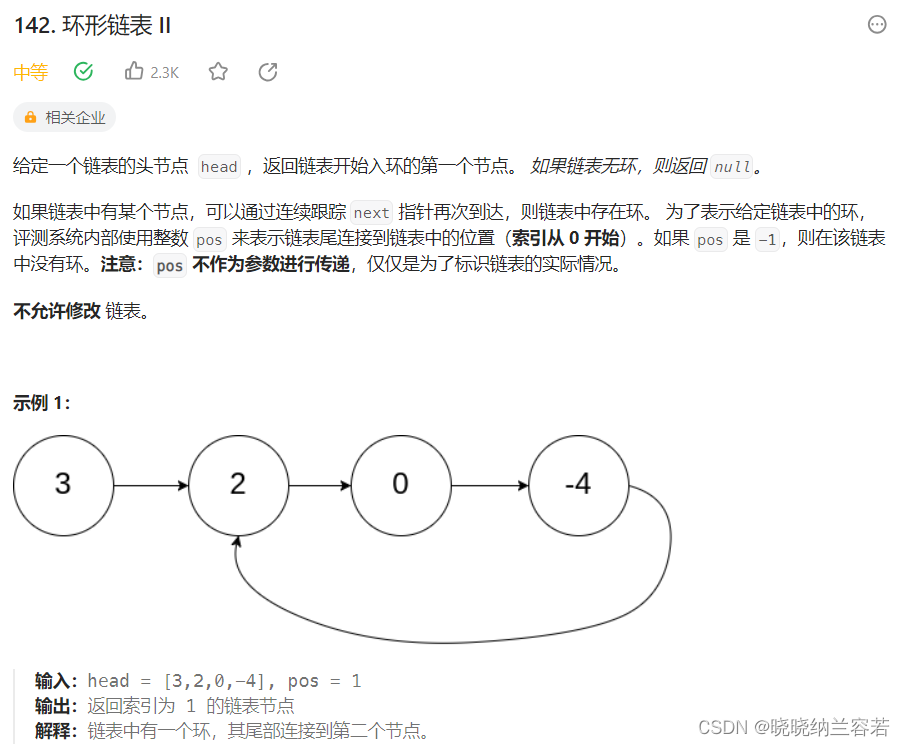
1--环形链表II

主要思路：

        快慢指针，快指针每次走两步，慢指针每次走一步；

        第一次相遇时，假设慢指针共走了 f 步，则快指针走了 2f 步；

        假设起点到环入口结点的长度为 a（不包括入口结点），环的结点数为 b；快指针比慢指针多走的步数肯定全在环中，则有 2f - f = f = nb；则慢指针共走了 nb 步；

        由于慢指针共走了 nb 步，而起点到环入口结点的步数为 a，则实际慢指针在环内走了 nb - a 步；

        此时让慢指针从起点重新出发走 a 步，每次走 1 步；快指针从相遇的地方出发，每次也走 1 步，快慢指针必然在环入口结点相遇；因此快指针相当于也走了 a 步，恰好与 nb - a 步互补，构成完整圈数的 nb 环；

#include <iostream>
#include <vector>

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(head == nullptr) return head;
        ListNode *slow = head;
        ListNode *fast = head;
        while(fast != NULL && fast->next != NULL){
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow) break; // 第一次相遇
        }
        if(fast == NULL || fast->next == NULL) return NULL; // 没有环
        // 从头开始走
        slow = head;
        while(slow != fast){
            slow = slow->next;
            fast = fast->next;
        }
        // 第二次相遇就是环的入口
        return slow;
    }
};

int main(int argc, char *argv[]) {
	// head = [3, 2, 0, -4], pos = 1
	ListNode *Node1 = new ListNode(3);
	ListNode *Node2 = new ListNode(2);
	ListNode *Node3 = new ListNode(0);
	ListNode *Node4 = new ListNode(-4);

	Node1->next = Node2;
	Node2->next = Node3;
	Node3->next = Node4;
	Node4->next = Node2;

	Solution S1;
	ListNode* res = S1.detectCycle(Node1);
	if(res != nullptr) std::cout << res->val << std::endl;
	else std::cout << "nullptr" << std::endl;
	return 0;
}

2--LRU缓存