问题 BW: 将邻接矩阵存储的图转换为邻接表存储的图,附加代码模式
内存限制:128 MB时间限制:1.000 S
评测方式:文本比较命题人:liuyong
提交:906解决:652
返回比赛提交提交记录侧边提交
题目描述
用邻接表法存储的图如下所示:
要求将邻接矩阵存储的图,改造为邻接表存储的图,并输出。
本题为附加代码模式,以下代码为自动附加在同学们提交的代码后面。在本题的提示中有代码框架,请同学们拷贝后,修改,再注释掉部分代码,最后提交。
// please comment the following code when you submit to OJ
int main(){
//freopen("/config/workspace/answer/test.in","r",stdin);
//freopen("/config/workspace/answer/test.out","w",stdout);
Graph g;
cin >> g.vexNumber;
for(int i=0;i<g.vexNumber;i++){
g.info[i] = (char)('a'+i);
for(int j=0;j<g.vexNumber;j++){
cin >> g.adjMatrix[i][j];
}
}
linkGraph G;
InitGraph(G,g);
PrintGraph(G);
DestroyGraph(G);
return 0;
}
输入
输入的第一行包含一个正整数n,表示图中共有n个顶点。其中n不超过50。 以后的n行中每行有n个用空格隔开的整数0或1,对于第i行的第j个0或1,1表示第i个顶点和第j个顶点有直接连接,0表示没有直接连接。当i和j相等的时候,保证对应的整数为0。 注意输入的邻接矩阵不一定为对称矩阵,即输入的图一定是可能是有向图,也可能是无向图。
输出
对每个节点,输出节点字母,及其所有的邻接点
样例输入 复制
7
0 0 0 0 0 1 1
0 0 1 0 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 0 0
0 0 0 1 0 0 0
0 0 0 0 1 0 1
0 1 0 1 0 0 0样例输出 复制
a --> g --> f
b --> c
c --> e
d
e --> d
f --> g --> e
g --> d --> b 提示
代码框架如下:
#include <iostream>
#include <cstdio>
using namespace std;
#define MAX_SIZE 100
// 邻接矩阵存储的图
struct Graph{
int vexNumber;
string info[MAX_SIZE];
int adjMatrix[MAX_SIZE][MAX_SIZE];
};
// 弧结点定义
struct ArcNode
{
int weight; // 弧上的信息部分
int adj; // 邻接点的序号
ArcNode *nextarc;
};
// 顶点结点定义
struct VexNode
{
string Info; // 顶点上的信息部分
ArcNode *firstarc; // 弧链头指针
};
// 邻接表结构的图的定义
struct linkGraph
{
VexNode *vexes;
int vexnumber;
};
int InitGraph(linkGraph &G, int vexnumber)
{
G.vexes = new VexNode[vexnumber];
G.vexnumber = vexnumber;
for (int i = 0; i < vexnumber; i++)
G.vexes[i].firstarc = NULL;
return 0;
}
// 将邻接矩阵存储的图转换为邻接表存储的图
void InitGraph(linkGraph &G, const Graph& g){
}
int DestroyGraph(linkGraph &G)
{
for (int i = 0; i < G.vexnumber; i++)
{
while (G.vexes[i].firstarc != NULL)
{
ArcNode *p = G.vexes[i].firstarc;
G.vexes[i].firstarc = p->nextarc;
delete p;
}
}
delete[]G.vexes;
G.vexes = NULL;
G.vexnumber = 0;
return 0;
}
// 输出邻接表存储的图
void PrintGraph(const linkGraph& G){
}
// please comment the following code when you submit to OJ
int main(){
//freopen("/config/workspace/answer/test.in","r",stdin);
//freopen("/config/workspace/answer/test.out","w",stdout);
Graph g;
cin >> g.vexNumber;
for(int i=0;i<g.vexNumber;i++){
g.info[i] = (char)('a'+i);
for(int j=0;j<g.vexNumber;j++){
cin >> g.adjMatrix[i][j];
}
}
linkGraph G;
InitGraph(G,g);
PrintGraph(G);
DestroyGraph(G);
return 0;
}
#include<bits/stdc++.h>
using namespace std;
#define MAX_SIZE 100
struct Graph{
int vexNumber;
string info[MAX_SIZE];
int adjMatrix[MAX_SIZE][MAX_SIZE];
};
struct ArcNode
{
int weight;
int adj;
ArcNode *nextarc;
};
struct VexNode
{
string Info;
ArcNode *firstarc;
};
struct linkGraph
{
VexNode *vexes;
int vexnumber;
};
int InitGraph(linkGraph &G,int vexnumber)
{
G.vexes = new VexNode[vexnumber];
G.vexnumber = vexnumber;
for(int i=0;i<vexnumber;i++)
{
G.vexes[i].firstarc=NULL;
}
return 0;
}
void InitGraph(linkGraph &G,const Graph &g)
{
InitGraph(G,g.vexNumber);
for(int i=0;i<g.vexNumber;i++)
{
G.vexes[i].Info=g.info[i];
for(int j=0;j<g.vexNumber;j++)
{
if(g.adjMatrix[i][j]==1)
{
ArcNode *temp = new ArcNode;
temp->nextarc=G.vexes[i].firstarc;
G.vexes[i].firstarc=temp;
temp->weight=j;
}
}
}
}
int DestroyGraph(linkGraph &G)
{
for(int i=0;i<G.vexnumber;i++)
{
while(G.vexes[i].firstarc!=NULL)
{
ArcNode *p=G.vexes[i].firstarc;
G.vexes[i].firstarc = p->nextarc;
delete p;
}
}
delete[]G.vexes;
G.vexes=NULL;
G.vexnumber=0;
return 0;
}
void PrintGraph(const linkGraph & G)
{
for(int i=0;i<G.vexnumber;i++)
{
ArcNode *temp=G.vexes[i].firstarc;
cout<<G.vexes[i].Info<<" ";
while(temp!=NULL)
{
printf("--> %c ",temp->weight+'a');
temp=temp->nextarc;
}
cout<<endl;
}
}
// int main()
// {
// Graph g;
// cin>>g.vexNumber;
// for(int i=0;i<g.vexNumber;i++)
// {
// g.info[i]=(char)('a'+i);
// for(int j=0;j<g.vexNumber;j++)
// cin>>g.adjMatrix[i][j];
// }
// linkGraph G;
// InitGraph(G,g);
// PrintGraph(G);
// DestroyGraph(G);
// return 0;
// }问题 BX: 邻接表存储的图转化为邻接矩阵存储的图-附加代码模式
内存限制:128 MB时间限制:1.000 S
评测方式:文本比较命题人:liuyong
提交:818解决:559
返回比赛提交提交记录侧边提交
题目描述
邻接表和邻接矩阵,是两种最重要的,也是最基础的图的存储方式。同学们需要熟练掌握这两种方式的程序编写。
以上图为例,其对应的邻接表和邻接矩阵存储方式可以分别表示为:
(1)邻接表法
节点个数:7
节点信息:a b c d e f g
a-g-f
b-c
c-e
d
e-d
f-g-e
g-d
(2)邻接矩阵法
节点个数:7
节点信息:a b c d e f g
0 0 0 0 0 1 1
0 0 1 0 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 0 0
0 0 0 1 0 0 0
0 0 0 0 1 0 1
0 1 0 1 0 0 0
请编写程序将邻接表法存储的图,转化为邻接矩阵法存储的图,并输出
// please comment the following code when you submit to OJ
int main(){
// freopen("/config/workspace/answer/test.in","r",stdin);
linkGraph LG;
Graph G;
InputlinkGraph(LG);
PrintlinkGraph(LG);
linkGraph2Graph(LG,G);
printGraph(G);
DestroylinkGraph(LG);
return 0;
}
本题为附加代码模式,以上代码为自动附加在同学们提交的代码后面。在本题的提示中有代码框架,请同学们拷贝后,修改,再注释掉部分代码,最后提交。
输入
输入第一行为正整数n(n<100),表示图的节点个数。
接下来n行,表示每个节点的信息,还有以该节点为起点可以到达的其他点的边信息
约定:每个节点信息为小写字母a开始的连续n个字母
输出
首先输出邻接表
再输出由0,1组成的邻接矩阵
样例输入 复制
7
a-g-f
b-c
c-e
d
e-d
f-g-e
g-d样例输出 复制
a --> g --> f
b --> c
c --> e
d
e --> d
f --> g --> e
g --> d
0 0 0 0 0 1 1
0 0 1 0 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 0 0
0 0 0 1 0 0 0
0 0 0 0 1 0 1
0 0 0 1 0 0 0 提示
代码框架如下(注意里面有一些小错误需要修复):
#include <iostream>
#include <cstdio>
#include <stack>
#include <queue>
using namespace std;
#define MAX_SIZE 100
// 邻接矩阵存储的图
struct Graph
{
int vexNumber;
string vexInfo[MAX_SIZE];
int adjMatrix[MAX_SIZE][MAX_SIZE];
};
// 弧结点定义
struct ArcNode
{
int weight; // 弧上的信息部分
int adj; // 邻接点的序号
ArcNode *nextarc; // 下一条边
};
// 顶点结点定义
struct VexNode
{
string Info; // 顶点上的信息部分
ArcNode *firstarc; // 弧链头指针
};
// 邻接表结构的图的定义
struct linkGraph
{
VexNode *vexes; // 每个节点的邻接表
int vexnumber; // 节点数量
};
// 邻接表存储的图的初始化
int InitGraph(linkGraph &G, int vexnumber)
{
G.vexes = new VexNode[vexnumber];
G.vexnumber = vexnumber;
for (int i = 0; i < vexnumber; i++)
G.vexes[i].firstarc = NULL;
return 0;
}
// 构造边节点指针
ArcNode* getArcNode(int adj){
ArcNode* node = new ArcNode();
node->adj = adj;
node->nextarc = nullptr;
return node;
}
// 根据输入构造邻接表存储的图
void InputlinkGraph(linkGraph& LG){
}
// 将邻接表存储的图转化为邻接矩阵存储的图
void linkGraph2Graph(const linkGraph& LG, Graph& G){
}
// 输出邻接矩阵
void printGraph(const Graph& G){
}
// 邻接表存储的图的销毁
int DestroylinkGraph(linkGraph &G)
{
for (int i = 0; i < G.vexnumber; i++)
{
while (G.vexes[i].firstarc != NULL)
{
ArcNode *p = G.vexes[i].firstarc;
G.vexes[i].firstarc = p->nextarc;
delete p;
}
}
delete[] G.vexes;
G.vexes = NULL;
G.vexnumber = 0;
return 0;
}
// please comment the following code when you submit to OJ
int main(){
// freopen("/config/workspace/answer/test.in","r",stdin);
linkGraph LG;
Graph G;
InputlinkGraph(LG);
PrintlinkGraph(LG);
linkGraph2Graph(LG,G);
printGraph(G);
DestroylinkGraph(LG);
return 0;
}
#include<bits/stdc++.h>
#include<string.h>
using namespace std;
#define MAX_SIZE 100
struct Graph{
int vexNumber;
string vexinfo[MAX_SIZE];
int adjMatrix[MAX_SIZE][MAX_SIZE];
};
struct ArcNode
{
char weight;
int adj;
ArcNode *nextarc;
};
struct VexNode
{
string Info;
ArcNode *firstarc;
};
struct linkGraph
{
VexNode *vexes;
int vexnumber;
};
int InitGraph(linkGraph &G,int vexnumber)
{
G.vexes = new VexNode[vexnumber];
G.vexnumber = vexnumber;
for(int i=0;i<vexnumber;i++)
{
G.vexes[i].firstarc=NULL;
}
return 0;
}
ArcNode* getArcNode(int adj)
{
ArcNode* node = new ArcNode;
node->adj=adj;
node->nextarc=nullptr;
return node;
}
void InputlinkGraph(linkGraph& LG)
{
cin>>LG.vexnumber;
InitGraph(LG,LG.vexnumber);
for(int i=0;i<LG.vexnumber;i++)
{
string s;
cin>>s;
LG.vexes[i].Info=s[0];
stack<char>tempstack;
for(int j=1;j<s.length();j++)
{
if(s[j]!='-')
tempstack.push(s[j]);
}
while(tempstack.size()!=0)
{
ArcNode *temp=new ArcNode;
temp->nextarc=LG.vexes[i].firstarc;
LG.vexes[i].firstarc=temp;
temp->weight=tempstack.top();
tempstack.pop();
}
}
}
void linkGraph2Graph(const linkGraph&LG,Graph & G)
{
G.vexNumber=LG.vexnumber;
for(int i=0;i<LG.vexnumber;i++)
{
ArcNode *temp=LG.vexes[i].firstarc;
while(temp!=NULL)
{
G.adjMatrix[i][int(temp->weight-'a')]=1;
temp=temp->nextarc;
}
}
}
void PrintlinkGraph(const linkGraph&LG)
{
for(int i=0;i<LG.vexnumber;i++)
{
cout<<LG.vexes[i].Info<<" ";
ArcNode *temp = LG.vexes[i].firstarc;
while(temp!=NULL)
{
printf("--> %c ",temp->weight);
temp=temp->nextarc;
}
cout<<endl;
}
}
void printGraph(const Graph& G)
{
for(int i=0;i<G.vexNumber;i++)
{
for(int j=0;j<G.vexNumber;j++)
{
if(G.adjMatrix[i][j]==1)
cout<<1<<" ";
else
{
cout<<0<<" ";
}
}
cout<<endl;
}
}
int DestroylinkGraph(linkGraph &G)
{
for(int i=0;i<G.vexnumber;i++)
{
while(G.vexes[i].firstarc!=NULL)
{
ArcNode *p=G.vexes[i].firstarc;
G.vexes[i].firstarc = p->nextarc;
delete p;
}
}
delete[]G.vexes;
G.vexes=NULL;
G.vexnumber=0;
return 0;
}
// int main()
// {
// linkGraph LG;
// Graph G;
// InputlinkGraph(LG);
// PrintlinkGraph(LG);
// linkGraph2Graph(LG,G);
// printGraph(G);
// DestroyGraph(LG);
// return 0;
// }问题 BY: 邻接矩阵存储图的DFS(附加代码模式)
内存限制:128 MB时间限制:1.000 S
评测方式:文本比较命题人:2011014323
提交:2870解决:1873
返回比赛提交提交记录侧边提交
题目描述
深度优先搜索遍历类似于树的先序遍历,是树的先序遍历算法的推广。
其过程为:假设初始状态是图中所有顶点未曾被访问,则深度优先搜索可以从图中的某个顶点v出发,访问此顶点,然后依次从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到;
若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作为起始点,重复上述过程,直至图中所有顶点都被访问到为止。
在本题中,读入一个图的邻接矩阵(即数组表示),建立图并按照以上描述中的算法遍历所有顶点,输出遍历顶点的顺序。
本题为附加代码模式,以下代码将自动附加在同学们提交的代码后面。在本题的提示中有代码框架,请同学们拷贝后,修改,再注释掉部分代码,最后提交。
// please comment the following code when you submit to OJ
int main(){
// freopen("/config/workspace/answer/test.in","r",stdin);
// freopen("/config/workspace/answer/test.out","w",stdout);
Graph G;
cin >> G.vexNumber;
for(int i=0;i<G.vexNumber;i++){
G.vexInfo[i] = to_string(i);
for(int j=0;j<G.vexNumber;j++){
cin >> G.adjMatrix[i][j];
}
}
DFS(G);
return 0;
}
输入
输入的第一行包含一个正整数n,表示图中共有n个顶点。其中n不超过50。 以后的n行中每行有n个用空格隔开的整数0或1,对于第i行的第j个0或1,1表示第i个顶点和第j个顶点有直接连接,0表示没有直接连接。当i和j相等的时候,保证对应的整数为0。
输出
只有一行,包含n个整数,表示按照题目描述中的深度优先遍历算法遍历整个图的访问顶点顺序。每个整数后输出一个空格,并请注意行尾输出换行。
样例输入 复制
4
0 1 0 1
1 0 0 0
0 0 0 1
1 0 1 0样例输出 复制
0 1 3 2 提示
代码框架如下:
#include <iostream>
#include <string>
#include <cstdio>
#include <stack>
#include <queue>
using namespace std;
#define MAX_SIZE 100
// 邻接矩阵存储的图
struct Graph
{
int vexNumber;
string vexInfo[MAX_SIZE];
int adjMatrix[MAX_SIZE][MAX_SIZE];
};
// 查找v0的未被访问的邻接点
int findAdjVex(const Graph& G, int v0, int visited[]){
}
// 以顶点v0为起点,进行一趟DFS
void DFS(const Graph& G, int v0, int visited[]){
// 第一步: 先访问v0,标记已访问
// 第二步: 再对v0的所有未被访问的邻接点进行DFS
}
// 对整个图进行DFS
void DFS(const Graph& G){
// 第一步:初始化visited数组
// 第二步:以每个未被遍历的顶点为起点,进行DFS
}
// please comment the following code when you submit to OJ
int main(){
// freopen("/config/workspace/answer/test.in","r",stdin);
// freopen("/config/workspace/answer/test.out","w",stdout);
Graph G;
cin >> G.vexNumber;
for(int i=0;i<G.vexNumber;i++){
G.vexInfo[i] = to_string(i);
for(int j=0;j<G.vexNumber;j++){
cin >> G.adjMatrix[i][j];
}
}
DFS(G);
return 0;
}
#include<bits/stdc++.h>
#include<string.h>
using namespace std;
#define MAX_SIZE 100
struct Graph{
int vexNumber;
string vexInfo[MAX_SIZE];
int adjMatrix[MAX_SIZE][MAX_SIZE];
};
//坑我是吧??
// int findAdjVex(const Graph& G,int v0,int visited[])
// {
// for(int j=0;j<G.vexNumber;j++)
// {
// if(G.adjMatrix[v0][j]==1&&visited[j]==0)
// return j;
// }
// return 0;
// }
void DFS(const Graph& G,int v0,int visited[])
{
cout<<v0<<" ";
visited[v0]=1;
for(int j=0;j<G.vexNumber;j++)
{
if(G.adjMatrix[v0][j]==1&&visited[j]==0)
DFS(G,j,visited);
}
}
void DFS(const Graph& G)
{
int visited[MAX_SIZE];
for(int i=0;i<G.vexNumber;i++)
visited[i]=0;
for(int i=0;i<G.vexNumber;i++)
{
if(visited[i]==0)
DFS(G,i,visited);
}
}
// int main()
// {
// Graph G;
// cin>>G.vexNumber;
// for(int i=0;i<G.vexNumber;i++)
// {
// G.vexinfo[i]=to_string(i);
// for(int j=0;j<G.vexNumber;j++)
// cin>>G.adjMatrix[i][j];
// }
// DFS(G);
// return 0;
// }问题 BZ: 邻接矩阵存储图的DFS-非递归算法(附加代码模式)
内存限制:128 MB时间限制:1.000 S
评测方式:文本比较命题人:liuyong
提交:582解决:517
返回比赛提交提交记录侧边提交
题目描述
深度优先搜索遍历类似于树的先序遍历,是树的先序遍历算法的推广。
其过程为:假设初始状态是图中所有顶点未曾被访问,则深度优先搜索可以从图中的某个顶点v出发,访问此顶点,然后依次从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到;
若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作为起始点,重复上述过程,直至图中所有顶点都被访问到为止。
在本题中,读入一个图的邻接矩阵(即数组表示),建立图并按照以上描述中的算法遍历所有顶点,输出遍历顶点的顺序。
DFS的非递归算法实现也类似于树的先序遍历算法的非递归实现,用栈来存储节点,如果该节点“完成”了,即所有邻接点都已经被访问,那么该节点将从栈中退出。
本题为附加代码模式,以下代码将自动附加在同学们提交的代码后面。在本题的提示中有代码框架,请同学们拷贝后,修改,再注释掉部分代码,最后提交。
// please comment the following code when you submit to OJ
int main(){
// freopen("/config/workspace/answer/test.in","r",stdin);
// freopen("/config/workspace/answer/test.out","w",stdout);
Graph G;
cin >> G.vexNumber;
for(int i=0;i<G.vexNumber;i++){
G.vexInfo[i] = to_string(i);
for(int j=0;j<G.vexNumber;j++){
cin >> G.adjMatrix[i][j];
}
}
string str = DFS(G);
cout << str << endl;
return 0;
}
输入
输入的第一行包含一个正整数n,表示图中共有n个顶点。其中n不超过50。 以后的n行中每行有n个用空格隔开的整数0或1,对于第i行的第j个0或1,1表示第i个顶点和第j个顶点有直接连接,0表示没有直接连接。当i和j相等的时候,保证对应的整数为0。
输出
只有一行,包含n个整数,表示按照题目描述中的深度优先遍历算法遍历整个图的访问顶点顺序。每个整数后输出一个空格,并请注意行尾输出换行。
样例输入 复制
4
0 1 0 1
1 0 0 0
0 0 0 1
1 0 1 0样例输出 复制
0 1 3 2 提示
代码框架如下所示:
#include <iostream>
#include <string>
#include <cstdio>
#include <stack>
#include <queue>
using namespace std;
#define MAX_SIZE 100
// 邻接矩阵存储的图
struct Graph
{
int vexNumber;
string vexInfo[MAX_SIZE];
int adjMatrix[MAX_SIZE][MAX_SIZE];
};
// 查找v0的未被访问的邻接点
int findAdjVex(const Graph& G, int v0, int visited[]){
}
// 以顶点v0为起点,进行一趟DFS
string DFS(const Graph& G, int v0, int visited[]){
string result = "";
return result;
}
// 对整个图进行DFS
string DFS(const Graph& G){
string result = "";
// 第一步:初始化visited数组
// 第二步:以每个未被遍历的顶点为起点,进行DFS
return result;
}
// please comment the following code when you submit to OJ
int main(){
// freopen("/config/workspace/answer/test.in","r",stdin);
// freopen("/config/workspace/answer/test.out","w",stdout);
Graph G;
cin >> G.vexNumber;
for(int i=0;i<G.vexNumber;i++){
G.vexInfo[i] = to_string(i);
for(int j=0;j<G.vexNumber;j++){
cin >> G.adjMatrix[i][j];
}
}
string str = DFS(G);
cout << str << endl;
return 0;
}
#include<bits/stdc++.h>
#include<string.h>
using namespace std;
#define MAX_SIZE 100
struct Graph{
int vexNumber;
string vexInfo[MAX_SIZE];
int adjMatrix[MAX_SIZE][MAX_SIZE];
};
int findAdjVex(const Graph& G,int v0,int visited[])
{
for(int j=0;j<G.vexNumber;j++)
{
if(G.adjMatrix[v0][j]==1&&visited[j]==0)
return j;
}
return 0;
}
string DFS(const Graph& G,int v0,int visited[])
{
string result="";
result+=to_string(v0)+" ";
visited[v0]=1;
stack<int>tempstack;
tempstack.push(v0);
while(tempstack.size()!=0)
{
int temp=findAdjVex(G,tempstack.top(),visited);
if(temp!=0)
{
result+=to_string(temp)+" ";
visited[temp]=1;
tempstack.push(temp);
}
else
{
tempstack.pop();
}
}
return result;
}
string DFS(const Graph& G)
{
string result="";
int visited[MAX_SIZE];
for(int i=0;i<G.vexNumber;i++)
visited[i]=0;
for(int i=0;i<G.vexNumber;i++)
{
if(visited[i]==0)
result+=DFS(G,i,visited);
}
return result;
}
// int main()
// {
// Graph G;
// cin>>G.vexNumber;
// for(int i=0;i<G.vexNumber;i++)
// {
// G.vexInfo[i]=to_string(i);
// for(int j=0;j<G.vexNumber;j++)
// cin>>G.adjMatrix[i][j];
// }
// string str=DFS(G);
// cout<<str<<endl;
// return 0;
// }
问题 CA: 邻接矩阵存储图的BFS
内存限制:128 MB时间限制:1.000 S
评测方式:文本比较命题人:2011014323
提交:2599解决:1750
返回比赛提交提交记录侧边提交
题目描述
广度优先搜索遍历类似于树的按层次遍历的过程。
其过程为:假设从图中的某顶点v出发,在访问了v之后依次访问v的各个未曾被访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问,直至图中所有已被访问的顶点的邻接点都被访问到。
若此时图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作为起始点。重复上述过程,直至图中所有顶点都被访问到为止。
在本题中,读入一个图的邻接矩阵(即数组表示),建立图并按照以上描述中的算法遍历所有顶点,输出遍历顶点的顺序。
输入
输入的第一行包含一个正整数n,表示图中共有n个顶点。其中n不超过50。
以后的n行中每行有n个用空格隔开的整数0或1,对于第i行的第j个0或1,1表示第i个顶点和第j个顶点有直接连接,0表示没有直接连接。当i和j相等的时候,保证对应的整数为0。
输出
只有一行,包含n个整数,表示按照题目描述中的广度优先遍历算法遍历整个图的访问顶点顺序。每个整数后输出一个空格,并请注意行尾输出换行。
样例输入 复制
4
0 0 0 1
0 0 1 1
0 1 0 1
1 1 1 0样例输出 复制
0 3 1 2 #include<bits/stdc++.h>
#include<string.h>
using namespace std;
#define MAX_SIZE 100
struct Graph{
int vexNumber;
string vexInfo[MAX_SIZE];
int adjMatrix[MAX_SIZE][MAX_SIZE];
};
int findAdjVex(const Graph& G,int v0,int visited[])
{
for(int j=0;j<G.vexNumber;j++)
{
if(G.adjMatrix[v0][j]==1&&visited[j]==0)
return j;
}
return 0;
}
string DFS(const Graph& G,int v0,int visited[])
{
string result="";
result+=to_string(v0)+" ";
visited[v0]=1;
queue<int>tempstack;
tempstack.push(v0);
while(tempstack.size()!=0)
{
int temp=findAdjVex(G,tempstack.front(),visited);
if(temp!=0)
{
result+=to_string(temp)+" ";
visited[temp]=1;
tempstack.push(temp);
}
else
{
tempstack.pop();
}
}
return result;
}
string DFS(const Graph& G)
{
string result="";
int visited[MAX_SIZE];
for(int i=0;i<G.vexNumber;i++)
visited[i]=0;
for(int i=0;i<G.vexNumber;i++)
{
if(visited[i]==0)
result+=DFS(G,i,visited);
}
return result;
}
int main()
{
Graph G;
cin>>G.vexNumber;
for(int i=0;i<G.vexNumber;i++)
{
G.vexInfo[i]=to_string(i);
for(int j=0;j<G.vexNumber;j++)
cin>>G.adjMatrix[i][j];
}
string str=DFS(G);
cout<<str<<endl;
return 0;
}
问题 CB: 案例6-1.2:邻接表存储图的广度优先遍历
内存限制:128 MB时间限制:1.000 S
评测方式:文本比较命题人:admin
提交:629解决:575
返回比赛提交提交记录侧边提交
题目描述
一个图有n个节点编号从0至n-1和m条边编号从0至m-1。 输出从点x开始的广度优先遍历顺序。
输入
第一行为n、m、x。
接下来m行每行有一组u,v。表示点u可以到达点v,点v也可以到达点u。
输出
输出经过点的顺序。(输出字典序最小的答案)
样例输入 复制
7 9 5
0 3
0 2
0 4
3 1
3 2
4 5
1 5
2 5
5 6
样例输出 复制
5 1 2 4 6 3 0#include<bits/stdc++.h>
#include<string.h>
using namespace std;
#define MAX_SIZE 100
int n;
int a[100][100];
string result="";
int findAdjVex(int v0,int visited[])
{
int temp1=105;
int temp2=105;
int flag=0;
for(int j=0;j<n;j++)
{
if(a[j][v0]== 1 && visited[j]==0)
{
flag=1;
temp1=j;
break;
}
}
for(int j=0;j<n;j++)
{
if(a[v0][j]==1 && visited[j]==0)
{
temp2=j;
flag=1;
break;
}
}
if(flag)
return min(temp1,temp2);
else
return -1;
}
void DFS(int v0,int visited[])
{
result+=to_string(v0)+" ";
visited[v0]=1;
queue<int>tempstack;
tempstack.push(v0);
while(tempstack.size()!=0)
{
int temp=findAdjVex(tempstack.front(),visited);
if(temp!=-1)
{
result+=to_string(temp)+" ";
visited[temp]=1;
tempstack.push(temp);
}
else
{
tempstack.pop();
}
}
}
int main()
{
int m,x;
cin>>n>>m>>x;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
a[i][j]=0;
for(int i=0;i<m;i++)
{
int x,y;
cin>>x>>y;
a[x][y]=1;
}
int visited[100];
for(int i=0;i<n;i++)
visited[i]=0;
DFS(x,visited);
cout<<result<<endl;
}问题 CC: 邻接矩阵存储图的DFS完成序求解(附加代码模式)
内存限制:128 MB时间限制:1.000 S
评测方式:文本比较命题人:liuyong
提交:510解决:507
返回比赛提交提交记录侧边提交
题目描述
在对图进行深度优先遍历的过程中,如果一个节点p没有未被访问的邻接点,则将该节点p标记为“完成”状态。
请编写程序,求解一个图的深度优先遍历完成序。
本题为附加代码模式,以下代码将自动附加在同学们提交的代码后面。在本题的提示中有代码框架,请同学们拷贝后,修改,再注释掉部分代码,最后提交。
// please comment the following code when you submit to OJ
int main(){
// freopen("/config/workspace/answer/test.in","r",stdin);
// freopen("/config/workspace/answer/test.out","w",stdout);
Graph G;
cin >> G.vexNumber;
for(int i=0;i<G.vexNumber;i++){
G.vexInfo[i] = (char)('a'+ i);
for(int j=0;j<G.vexNumber;j++){
cin >> G.adjMatrix[i][j];
}
}
string str = DFS_finished(G);
cout << str << endl;
return 0;
}
输入
输入的第一行包含一个正整数n,表示图中共有n个顶点。其中n不超过26。
默认每个顶点对应的信息依次为从a到z的小写字母。
以后的n行中每行有n个用空格隔开的整数0或1,对于第i行的第j个0或1,1表示第i个顶点和第j个顶点有直接连接,0表示没有直接连接。当i和j相等的时候,保证对应的整数为0。
默认从a开始dfs,依次顺延
输出
只有一行,包含n个字母,表示按照题目描述中的深度优先遍历算法遍历整个图的访问顶点顺序。
样例输入 复制
7
0 0 0 0 0 0 1
0 0 1 0 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 0 1
0 0 0 1 0 0 0
0 0 0 0 1 0 1
0 1 0 0 0 0 0样例输出 复制
decbgaf提示
代码框架如下:
#include <iostream>
#include <string>
#include <cstdio>
#include <stack>
#include <queue>
using namespace std;
#define MAX_SIZE 100
// 邻接矩阵存储的图
struct Graph
{
int vexNumber;
string vexInfo[MAX_SIZE];
int adjMatrix[MAX_SIZE][MAX_SIZE];
};
// 查找v0的未被访问的邻接点
int findAdjVex(const Graph& G, int v0, int visited[]){
}
// 算法7-1: 以某个节点为起点求解DFS完成序的算法 (邻接矩阵)
string DFS_finished(const Graph &G, int v0, int visited[]){
}
// 算法7: DFS完成序的求解算法-邻接矩阵
string DFS_finished(const Graph &G){
}
// please comment the following code when you submit to OJ
int main(){
// freopen("/config/workspace/answer/test.in","r",stdin);
// freopen("/config/workspace/answer/test.out","w",stdout);
Graph G;
cin >> G.vexNumber;
for(int i=0;i<G.vexNumber;i++){
G.vexInfo[i] = (char)('a'+ i);
for(int j=0;j<G.vexNumber;j++){
cin >> G.adjMatrix[i][j];
}
}
string str = DFS_finished(G);
cout << str << endl;
return 0;
}
#include<bits/stdc++.h>
#include<string.h>
using namespace std;
#define MAX_SIZE 100
struct Graph
{
int vexNumber;
string vexInfo[MAX_SIZE];
int adjMatrix[MAX_SIZE][MAX_SIZE];
};
int findAdjVex(const Graph& G,int v0,int visited[])
{
for(int j=0;j<G.vexNumber;j++)
{
if(G.adjMatrix[v0][j]==1 && visited[j]==0)
return j;
}
return 0;
}
string DFS_finished(const Graph &G,int v0,int visited[])
{
string result="";
visited[v0]=1;
stack<int>tempstack;
tempstack.push(v0);
while(tempstack.size()!=0)
{
int temp=findAdjVex(G,tempstack.top(),visited);
if(temp!=0)
{
visited[temp]=1;
tempstack.push(temp);
}
else
{
result+=char(tempstack.top()+'a');
tempstack.pop();
}
}
return result;
}
string DFS_finished(const Graph &G)
{
string result="";
int visited[MAX_SIZE];
for(int i=0;i<G.vexNumber;i++)
visited[i]=0;
for(int i=0;i<G.vexNumber;i++)
{
if(visited[i]==0)
result+=DFS_finished(G,i,visited);
}
return result;
}
// int main()
// {
// Graph G;
// cin>>G.vexNumber;
// for(int i=0;i<G.vexNumber;i++)
// {
// G.vexInfo[i]=(char)('a'+i);
// for(int j=0;j<G.vexNumber;j++)
// cin>>G.adjMatrix[i][j];
// }
// string str=DFS_finished(G);
// cout<<str<<endl;
// return 0;
// }问题 CD: 案例6-1.1:DFS应用-计算可达城市对
内存限制:1024 MB时间限制:1.000 S
评测方式:文本比较命题人:admin
提交:124解决:271
返回比赛提交提交记录侧边提交
题目描述
共有N个城市编号1到N和M条路编号1到M。
第i条路可以从城市Ai通往Bi,但不能从Bi通往Ai。
你计划从某个城市出发经过X(X>=0)条路到某个城市,即计划从某个城市经过任意条路到另一个城市,终点可以是出发的城市。
请计算有多少对城市可以作为你的起点和终点。
输入
第一行为N和M。
接下来M行,每行有一对城市Ai和Bi
输出
请计算有多少对城市可以作为你的起点和终点。
样例输入 复制
3 3
1 2
2 3
3 2
样例输出 复制
7
提示
2≤N≤2000
0≤M≤min(2000,N(N−1))
1≤Ai,Bi≤N
Ai≠Bi
样例解释:1城可选择去的城市(1,2,3),2城可选择(2,3),3城可选择(2,3),共七种选择
#include<bits/stdc++.h>
#include<string.h>
using namespace std;
#define MAX_SIZE 100
int a[2005][2005];
// struct Graph
// {
// int vexNumber;
// string vexInfo[MAX_SIZE];
// int adjMatrix[MAX_SIZE][MAX_SIZE];
// };
// int findAdjVex(int v0,int visited[])
// {
// for(int j=1;j<n;j++)
// {
// if(a[v0][j]==1 && visited[j]==0)
// return j;
// }
// return 0;
// }
// string DFS_finished(const Graph &G,int v0,int visited[])
// {
// string result="";
// visited[v0]=1;
// stack<int>tempstack;
// tempstack.push(v0);
// while(tempstack.size()!=0)
// {
// int temp=findAdjVex(G,tempstack.top(),visited);
// if(temp!=0)
// {
// visited[temp]=1;
// tempstack.push(temp);
// }
// else
// {
// result+=char(tempstack.top()+'a');
// tempstack.pop();
// }
// }
// return result;
// }
// string DFS_finished(const Graph &G)
// {
// string result="";
// int visited[MAX_SIZE];
// for(int i=0;i<G.vexNumber;i++)
// visited[i]=0;
// for(int i=0;i<G.vexNumber;i++)
// {
// if(visited[i]==0)
// result+=DFS_finished(G,i,visited);
// }
// return result;
// }
// int main()
// {
// Graph G;
// cin>>G.vexNumber;
// for(int i=0;i<G.vexNumber;i++)
// {
// G.vexInfo[i]=(char)('a'+i);
// for(int j=0;j<G.vexNumber;j++)
// cin>>G.adjMatrix[i][j];
// }
// string str=DFS_finished(G);
// cout<<str<<endl;
// return 0;
// }
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
a[i][j]=0;
}
for(int i=0;i<m;i++)
{
int x,y;
cin>>x>>y;
a[x][y]=1;
}
int ans=0;
queue<int>tempqueue;
for(int i=1;i<=n;i++)
{
int len=0;
tempqueue.push(i);
len++;
int visited[2005];
for(int j=0;j<=n;j++)
visited[j]=0;
visited[i]=1;
while(tempqueue.size()!=0)
{
int temp=tempqueue.front();
tempqueue.pop();
for(int j=1;j<=n;j++)
{
if(a[temp][j]==1 && visited[j]==0)
{
visited[j]=1;
tempqueue.push(j);
len++;
}
}
}
ans+=len;
}
cout<<ans<<endl;
}问题 CE: 案例6-1.3:哥尼斯堡的“七桥问题”
内存限制:128 MB时间限制:20.000 S
评测方式:文本比较命题人:admin
提交:150解决:228
返回比赛提交提交记录侧边提交
题目描述
哥尼斯堡是位于普累格河上的一座城市,它包含两个岛屿及连接它们的七座桥,如下图所示。
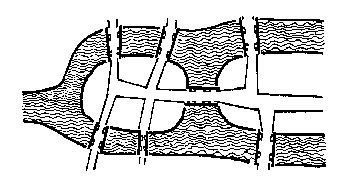
可否走过这样的七座桥,而且每桥只走过一次?瑞士数学家欧拉(Leonhard Euler,1707—1783)最终解决了这个问题,并由此创立了拓扑学。
这个问题如今可以描述为判断欧拉回路是否存在的问题。欧拉回路是指不令笔离开纸面,可画过图中每条边仅一次,且可以回到起点的一条回路。现给定一个无向图,问是否存在欧拉回路?
输入
输入第一行给出两个正整数,分别是节点数N (1≤N≤1000)和边数M;随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个节点的编号(节点从1到N编号)。
输出
若欧拉回路存在则输出1,否则输出0。
样例输入 复制
6 10
1 2
2 3
3 1
4 5
5 6
6 4
1 4
1 6
3 4
3 6样例输出 复制
1
#include<bits/stdc++.h>
#include<string.h>
using namespace std;
#define MAX_SIZE 100
int a[2005][2005];
// struct Graph
// {
// int vexNumber;
// string vexInfo[MAX_SIZE];
// int adjMatrix[MAX_SIZE][MAX_SIZE];
// };
// int findAdjVex(int v0,int visited[])
// {
// for(int j=1;j<n;j++)
// {
// if(a[v0][j]==1 && visited[j]==0)
// return j;
// }
// return 0;
// }
// string DFS_finished(const Graph &G,int v0,int visited[])
// {
// string result="";
// visited[v0]=1;
// stack<int>tempstack;
// tempstack.push(v0);
// while(tempstack.size()!=0)
// {
// int temp=findAdjVex(G,tempstack.top(),visited);
// if(temp!=0)
// {
// visited[temp]=1;
// tempstack.push(temp);
// }
// else
// {
// result+=char(tempstack.top()+'a');
// tempstack.pop();
// }
// }
// return result;
// }
// string DFS_finished(const Graph &G)
// {
// string result="";
// int visited[MAX_SIZE];
// for(int i=0;i<G.vexNumber;i++)
// visited[i]=0;
// for(int i=0;i<G.vexNumber;i++)
// {
// if(visited[i]==0)
// result+=DFS_finished(G,i,visited);
// }
// return result;
// }
// int main()
// {
// Graph G;
// cin>>G.vexNumber;
// for(int i=0;i<G.vexNumber;i++)
// {
// G.vexInfo[i]=(char)('a'+i);
// for(int j=0;j<G.vexNumber;j++)
// cin>>G.adjMatrix[i][j];
// }
// string str=DFS_finished(G);
// cout<<str<<endl;
// return 0;
// }
int main()
{
int n,m;
cin>>n>>m;
int flag=1;
if(m==0)
{
if(n==1)
cout<<1;
else
cout<<0;
return 0;
}
while(m--)
{
int x,y;
cin>>x>>y;
a[x][y]=1;
a[y][x]=1;
}
for(int i=1;i<=n;i++)
{
int nodes=0;
for(int j=1;j<=n;j++)
{
if(a[i][j]==1)
nodes++;
}
if(nodes%2!=0)
{
flag=0;
break;
}
}
if(flag)
cout<<1;
else
{
cout<<0;
}
}问题 CF: 案例6-1.4:地下迷宫探索
内存限制:10 MB时间限制:1.000 S
评测方式:文本比较命题人:admin
提交:109解决:237
返回比赛提交提交记录侧边提交
题目描述
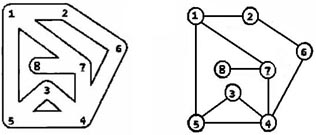
地道战是在抗日战争时期,在华北平原上抗日军民利用地道打击日本侵略者的作战方式。地道网是房连房、街连街、村连村的地下工事,如下图所示。
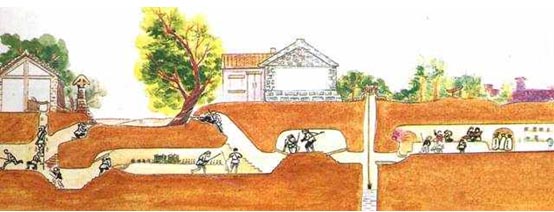
我们在回顾前辈们艰苦卓绝的战争生活的同时,真心钦佩他们的聪明才智。在现在和平发展的年代,对多数人来说,探索地下通道或许只是一种娱乐或者益智的游戏。本实验案例以探索地下通道迷宫作为内容。
假设有一个地下通道迷宫,它的通道都是直的,而通道所有交叉点(包括通道的端点)上都有一盏灯和一个开关。请问你如何从某个起点开始在迷宫中点亮所有的灯并回到起点?
输入
输入第一行给出三个正整数,分别表示地下迷宫的节点数N(1<N≤1000,表示通道所有交叉点和端点)、边数M(≤3000,表示通道数)和探索起始节点编号S(节点从1到N编号)。随后的M行对应M条边(通道),每行给出一对正整数,分别是该条边直接连通的两个节点的编号。
输出
若可以点亮所有节点的灯,则输出从S开始并以S结束的包含所有节点的序列,序列中相邻的节点一定有边(通道);否则虽然不能点亮所有节点的灯,但还是输出点亮部分灯的节点序列,最后输出0,此时表示迷宫不是连通图。
由于深度优先遍历的节点序列是不唯一的,为了使得输出具有唯一的结果,我们约定以节点小编号优先的次序访问(点灯)。在点亮所有可以点亮的灯后,以原路返回的方式回到起点。
样例输入 复制
6 8 1
1 2
2 3
3 4
4 5
5 6
6 4
3 6
1 5样例输出 复制
1 2 3 4 5 6 5 4 3 2 1#include<bits/stdc++.h>
using namespace std;
int a[1005][1005];
int n;
void dfs(int s,int visited[])
{
visited[s]=1;
for(int i=1;i<=n;i++)
{
if(a[s][i]==1 && visited[i]==0)
{
cout<<i<<" ";
dfs(i,visited);
cout<<s<<" ";
}
}
}
int main()
{
int m,s;
cin>>n>>m>>s;
while(m--)
{
int x,y;
cin>>x>>y;
a[x][y]=1;
a[y][x]=1;
}
cout<<s<<" ";
int visited[1005];
for(int i=1;i<=n;i++)
visited[i]=0;
dfs(s,visited);
for(int i=1;i<=n;i++)
{
if(!visited[i])
{
cout<<0;
break;
}
}
return 0;
}问题 CG: 基础实验6-2.3:拯救007
内存限制:128 MB时间限制:1.000 S
评测方式:文本比较命题人:admin
提交:91解决:226
返回比赛提交提交记录侧边提交
题目描述
在老电影“007之生死关头”(Live and Let Die)中有一个情节,007被毒贩抓到一个鳄鱼池中心的小岛上,他用了一种极为大胆的方法逃脱 —— 直接踩着池子里一系列鳄鱼的大脑袋跳上岸去!(据说当年替身演员被最后一条鳄鱼咬住了脚,幸好穿的是特别加厚的靴子才逃过一劫。)
设鳄鱼池是长宽为100米的方形,中心坐标为 (0, 0),且东北角坐标为 (50, 50)。池心岛是以 (0, 0) 为圆心、直径15米的圆。给定池中分布的鳄鱼的坐标、以及007一次能跳跃的最大距离,你需要告诉他是否有可能逃出生天。
输入
首先第一行给出两个正整数:鳄鱼数量 N(≤100)和007一次能跳跃的最大距离 D 。随后 N 行,每行给出一条鳄鱼的 (x,y ) 坐标。
注意:不会有两条鳄鱼待在同一个点上。
输出
如果007有可能逃脱,就在一行中输出"Yes",否则输出"No"。
样例输入 复制
14 20
25 -15
-25 28
8 49
29 15
-35 -2
5 28
27 -29
-8 -28
-20 -35
-25 -20
-13 29
-30 15
-35 40
12 12样例输出 复制
Yes提示
思考:
用广度优先搜索是否可以解决问题?
什么时候要存图解决问题,什么时候不要?
#include<bits/stdc++.h>
using namespace std;
int flag=0;
int n;
int d;
struct info
{
int x,y;
}a[101];
int dfs(int index,int visited[])
{
visited[index]=1;
if(a[index].x-d<=-50 || a[index].y-d<=-50 || a[index].x+d>=50 || a[index].y+d>=50)
{
flag=1;
return 0;
}
for(int i=0;i<n;i++)
{
if(visited[i]==0 && pow(a[index].x-a[i].x,2)+pow(a[index].y-a[i].y,2)<=d*d)
dfs(i,visited);
}
return 0;
}
int main()
{
cin>>n>>d;
for(int i=0;i<n;i++)
{
cin>>a[i].x>>a[i].y;
}
if(d>=50)
{
cout<<"Yes"<<endl;
return 0;
}
int visited[101];
for(int i=0;i<n;i++)
visited[i]=0;
for(int i=0;i<n;i++)
{
if(visited[i]==0 && pow(a[i].x,2)+pow(a[i].y,2)<=pow(d+7.5,2))
dfs(i,visited);
}
if(flag==1)
cout<<"Yes"<<endl;
else
{
cout<<"No"<<endl;
}
return 0;
}


![[附源码]计算机毕业设计Python第三方游戏零售平台(程序+源码+LW文档)](https://img-blog.csdnimg.cn/ddc3e6ce45714a0998add4c465841949.png)



![[附源码]Python计算机毕业设计Django智能衣橱APP](https://img-blog.csdnimg.cn/7d13634c36e84acb8f6feb5dcd9cad52.png)