第六章 关系数据库理论
6.1 问题的提出
-
关系模式的表示
关系模式由五部分组成,是一个五元组:R(U,D,DOM,F)。(1
- 关系名R是符号化的元组语义。
- U为一组属性。
- D为属性组U中的属性所来自的域。
- DOM为属性到域的映射。
- F为属性组U上的一组数据依赖。
-
说明
- 由于D、DOM与模式设计关系不大,因此在本章中把关系模式看作一个三元组:R<U,F>
- 当且仅当U上的一个关系r满足F时,r称为关系模式R<U,F>的一个关系。
- 作为一个二维表,关系要符合一个最基本的条件:每一个分量必须是不可分的数据项。满足了这个条件的关系模式就属于第一范式(1NF)。
-
数据依赖
数据依赖是一个关系内部属性与属性之间的一种约束关系,是通过属性间值的相等与否体现出来的数据间相互联系。
- 数据依赖的主要类型:
- 函数依赖(Functional Dependency,简记为FD)。
- 多值依赖(Mu!ti-Valued Dependency,简记为M
- 问题
- 数据冗余
- 更新异常
- 插入异常
- 删除异常
- 数据依赖的主要类型:
6.2 规范化
6.2.1 函数依赖
定义6.1设R(U)是属性集U上的关系模式,X,Y是U的子集。若对于R(U)的任意一个可能的关系r,r中不可能存在两个元组在X上的属性值相等,而在Y上的属性值不等,则称X函数确定Y或Y函数依赖于X,记作X→Y。
-
术语和记号
-
X → \rightarrow →Y,但Y ⊈ \nsubseteq ⊈X,则称X$\rightarrow $Y是非平凡的函数依赖。
-
X→Y,但Y ⊆ \subseteq ⊆X,则称X→Y是平凡的函数依赖。
对于任一关系模式,平凡函数依赖都是必然成立的,它不反映新的语义。若不特别声明,总是讨论非平凡的函数依赖。·
-
若X→y,则X称为这个函数依赖的决定属性组,也称为决定因素(determinant)。
-
若X→Y,Y→X,则记作X ← → \leftarrow \rightarrow ←→Y。
-
若Y不函数依赖于X,则记作X→Y。
-

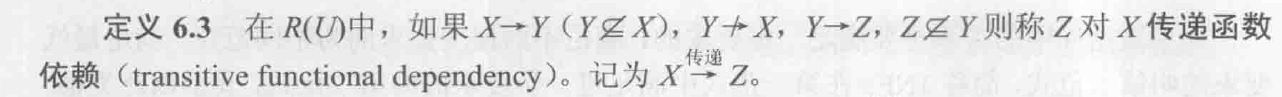
6.2.2 码


6.2.3 范式
关系数据库中的关系是要满足一定要求的,满足不同程度要求的为不同范式。满足最低要求的叫第一范式,简称1NF;在第一范式中满足进一步要求的为第二范式,其余以此类推。

- 规范化
- 一个低一级范式的关系模式通过模式分解(schemadecomposition)可以转换为若干个高一级范式的关系模式的集合,这种过程就叫规范化(normalization)。
6.2.4 2NF
- 若RE ∈ \in ∈NF,且每一个非主属性完全函数依赖于任何一个候选码,则RE$\in $2NF。
- 一个关系模式R不属于2NF,就会产生以下几个问题:
- 插入异常
- 删除异常
- 修改复杂
- 解决方法:
- 用投影分解把关系模式S-L-C分解成两个关系模式。
6.2.5 3NF

不能存在传递依赖
6.2.6 BCNF

- 由BCNF的定义可以得到结论,一个满足BCNF的关系模式有:
- 所有非主属性对每一个码都是完全函数依赖。
- 所有主属性对每一个不包含它的码也是完全函数依赖。
- 没有任何属性完全函数依赖于非码的任何一组属性。
6.2.7 多值依赖


- 多值依赖的性质
- 多值依赖具有对称性:若x→→Y,则X→→Z,其中
Z=U-X-Y - 多值依赖具有传递性:若X→→Y,Y→→Z,则X→→Z-Y。
- 函数依赖是多值依赖的特殊情况:若x→Y,则 X→→Y。
- 若x→→Y,X→→Z,则x→→YZ。
- 若x→→Y,X→→Z,则X→→Y ∩ \cap ∩Z。
- 若X→→Y,X→→Z,则X→→Y-Z,X→→Z-Y。
- 多值依赖具有对称性:若x→→Y,则X→→Z,其中

6.2.8 4NF

- 说明
- 4NF是限制关系模式的属性之间不允许有非平凡且非函数依赖的多值依赖。4NF所允许的非平凡多值依赖实际是函数依赖。
- 如果一个关系模式是4NF,则必为BCNF。
- 在关系WSC中,W→→S,W→→C,他们都是非平凡多值依赖。而W不是码,关系模式WSC的码是(W,S,C),即AlI-key,因此WSC4NF。可以把WSC分解成WS(W,S),WC(W,C),WSE4NF,WCE4NF。
6.2.9 小结

6.3 数据依赖的公理系统




定理6.2 Armstrong公理系统是有效的、完备的。


- 定理6.3
- 每一个函数依赖集F均等价于一个极小函数依赖集 F m F_m Fm。此$F_m $称为F的最小依赖集。
6.4 模式的分解

6.4.1 模式分解的三个定义
- 对于一个模式的分解是多种多样的,但是分解后产生的模式应与原模式等价。
- 等价
- 分解具有无损连接性(lossless join)。
- 分解要保持函数依赖(preserve functional dependency)。
- 分解既要保持函数依赖,又要具有无损连接性。
- 等价