在这里插入图片描述

欢迎来到我的：世界

希望作者的文章对你有所帮助，有不足的地方还请指正，大家一起学习交流 !

前言
堆的时间复杂度
- 向下调整算法的时间复杂度
- 向上调整算法的时间复杂度
堆的应用
- 堆排序
- TOP—K问题
- 链式二叉树
- - 二叉树的节点：
  - 初始化节点
  - 实现链式二叉树
- 二叉树的概念：
- - 二叉树的遍历
  - - 前序遍历
    - 中序遍历
    - 后序遍历
    - 层序遍历
总结

前言

该篇文章写到主要是：堆排序、 TOP-K问题、二叉树链式结构的实现、二叉树的遍历等等；如果有朋友还不太了解堆以及二叉树可以翻看我的上一篇博客：堆和二叉树的概念；
最后老铁们准备发车喽！！！

堆的时间复杂度

紧接上一篇博客，我们刚刚实现了堆的实现，还没有拿他做点有意义的事情呢 ,咱们马上开始👉
如果问你：建堆的时间复杂度是多少？

实现堆有有两种方法：向下调整算法和向上调整算法，但是这两种方法有区别吗？哪个算法的时间复杂度更好呢？
接下来我们来带着问题进入下方：

向下调整算法的时间复杂度

时间复杂度就是看其最坏的情况，因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值，多几个节点不影响最终结果)：

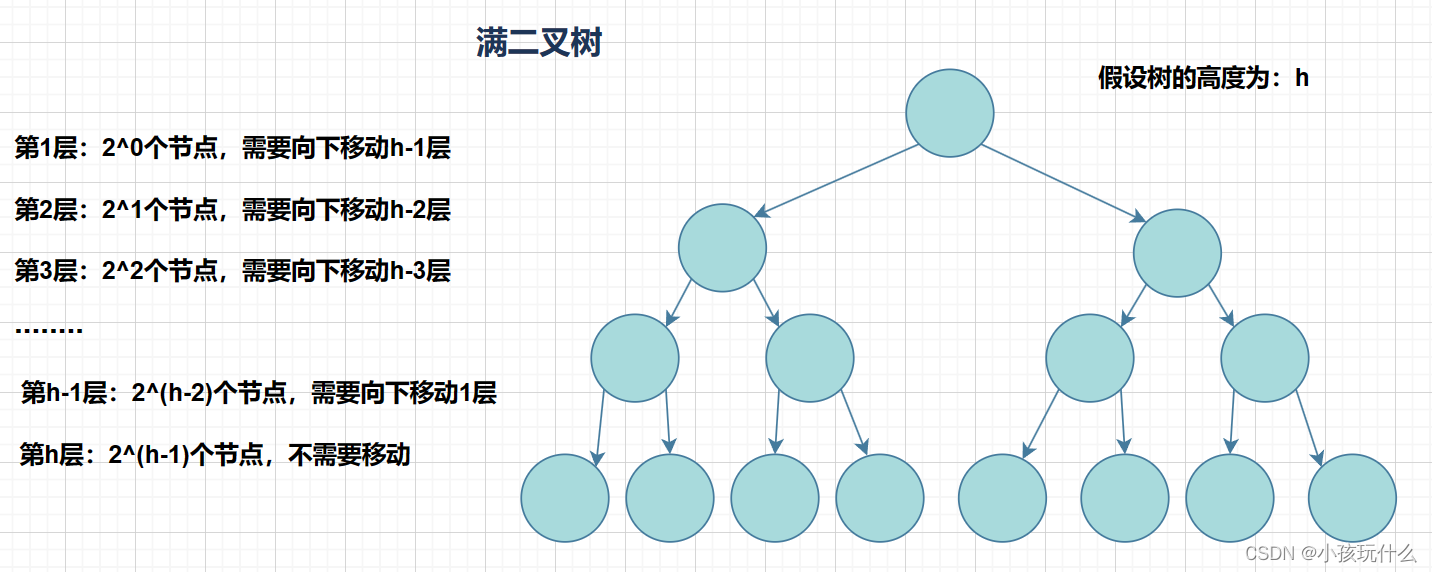
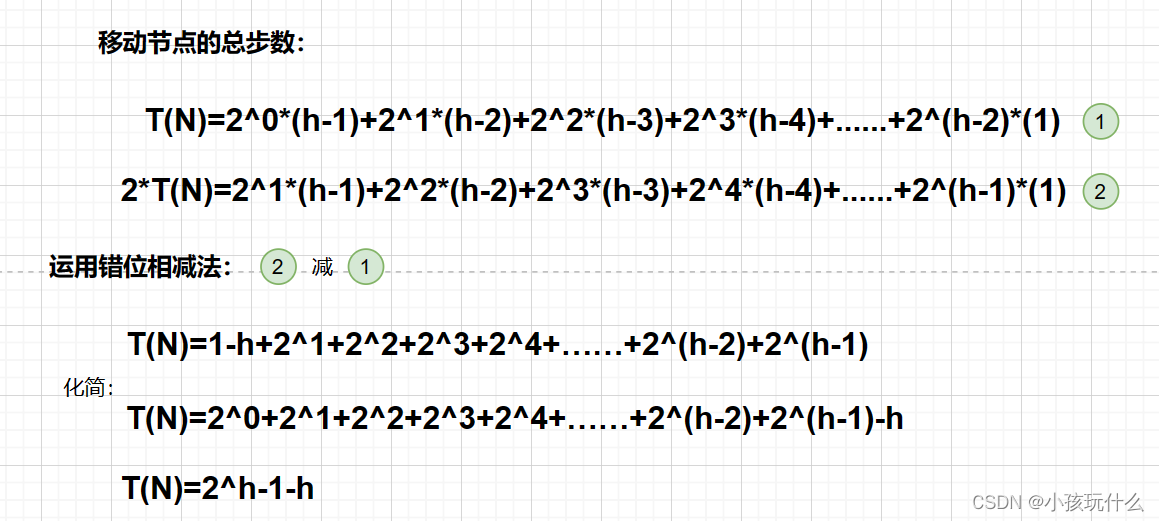
在这里插入图片描述

由于我们已经知道满二叉树结点和层数的关系：N=2^h-1可转化为h=log2(N+1)(ps：Log2(n+1)是log以2为底，n+1为对数)

知道了这层关系可以推出：
T(N)= N-log2(N+1)~ N (约等于)
所以向下调整算法的时间复杂度：O(N)。

向上调整算法的时间复杂度

向上调整算法的时间复杂度比向下调整算法要慢；如何得出呢？
同样的情况，利用的满二叉树来估计其时间复杂度；
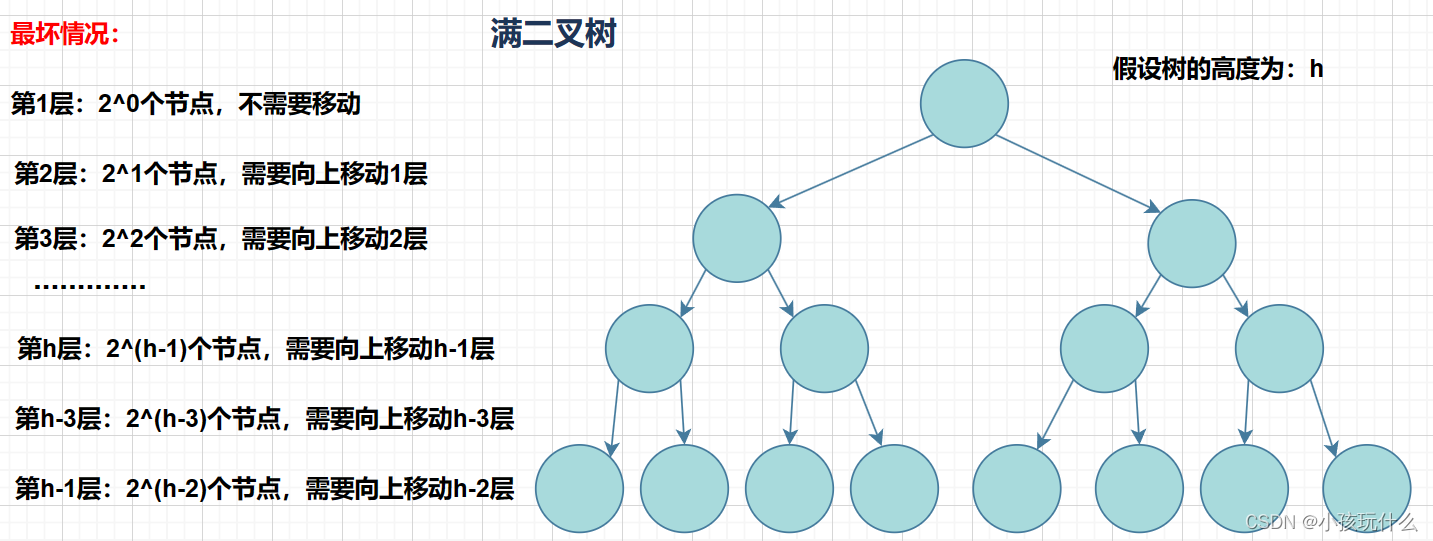
在这里插入图片描述
a1(1-q^n)/(1-q)
得出T(N)=2^h *(h-1) - 2*(1-2^h)进行化简：T(N)=2^h*(h+1)-2

可转化为：
T(N)=2^h*(h+1)-2=(N+1)*(log2(N+1)+1)-2(ps：Log2(n+1)是log以2为底，n+1为对数)
T(N)=(N+1)*(log2(N+1)+1)-2 ~ N*log2(N)(ps：Log2(N)是log以2为底，N为对数)
所以向上调整算法的时间复杂度是：O(N*logN)。

堆的应用

堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

1. 建堆
- 升序—建大堆
- 降序—建小堆
2. 利用堆删除思想来进行排序

建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。
就拿升序来说：
实现升序怎么完成呢？
首先要明白升序是建大堆；
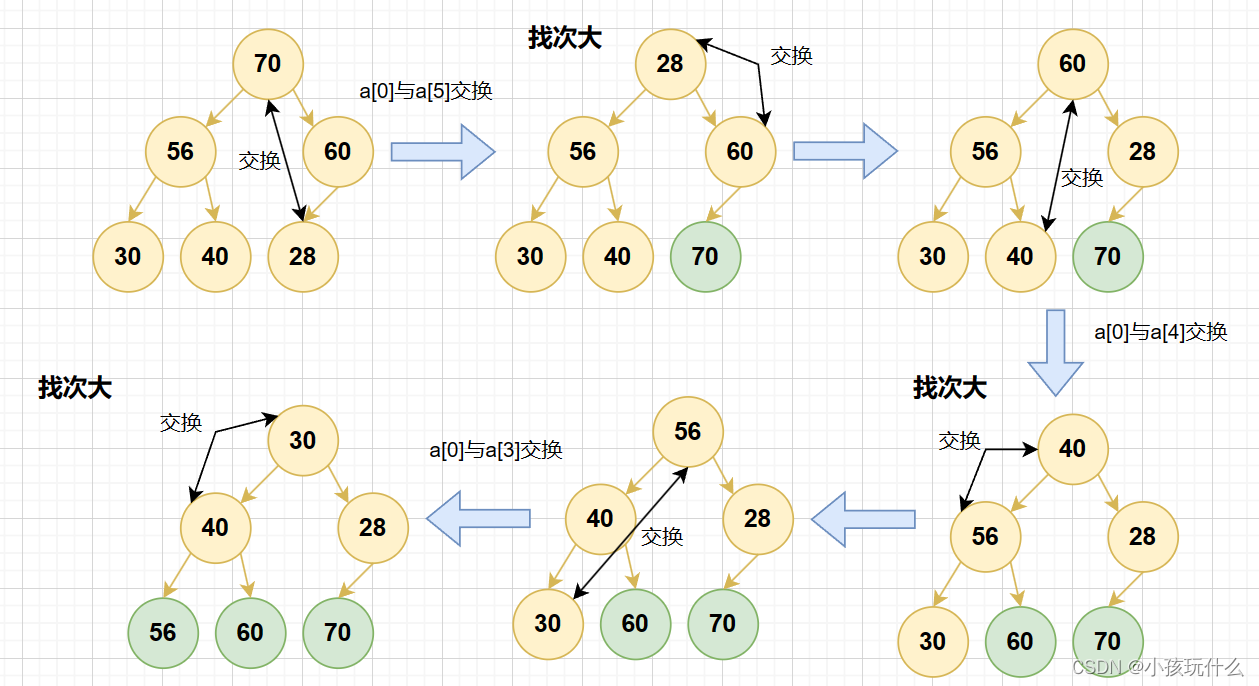
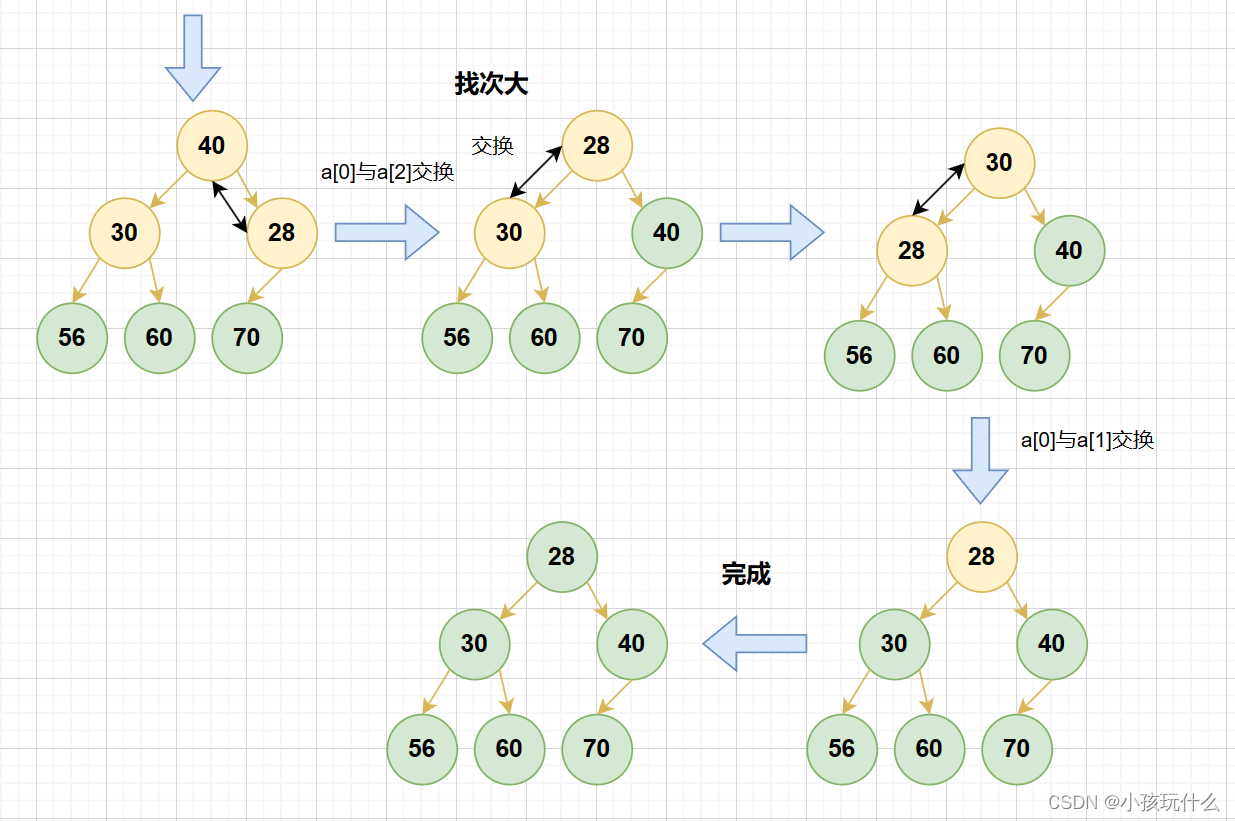
在这里插入图片描述

在这里插入图片描述
具体代码实现：

void HeapSort(int* a, int n)
{
	// 升序 -- 建大堆
	// 降序 -- 建小堆
	
	// 建堆--向上调整建堆--O(N*logN)
	//for (int i = 1; i < n; i++)
	//{
	//	AdjustUp(a, i);
	//}

	// 建堆--向下调整建堆 --O(N)
	for (int i = (n-1-1)/2; i >= 0; --i)
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);

		// 再调整，选出次小的数
		AdjustDown(a, end, 0);

		--end;
	}
}

TOP—K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等；
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能
数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

1. 用数据集合中前K个元素来建堆
- 前k个最大的元素，则建小堆
- 前k个最小的元素，则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
举个列子：有随机100万个数储存在堆中(条件：每个元素都在int的范围内)，现在需要找出最大或最小的5个数，如果全部进行堆排序，计算机的要算炸了，肯定不行；这就需要我们上面的思路：
如果要求出这组数据中最大的前K个数，就取数据的前K个元素来建小堆，假设是在所有数据中最大的前K个；在剩下的n-k个数据中，依次对小堆的第一个元素进行比较，如果比小堆的第一个元素还小就不可能是所有数据中最大的K个中的一个，如果比小堆的第一个元素大，那就让其代替小堆第一个的位置，在进行向下调整，让小堆中最小的那个元素到堆顶来，然后就再次比较下一个，直到所有元素都比完，那就代表堆中剩余的K个元素就是所求的前K个最大的元素。

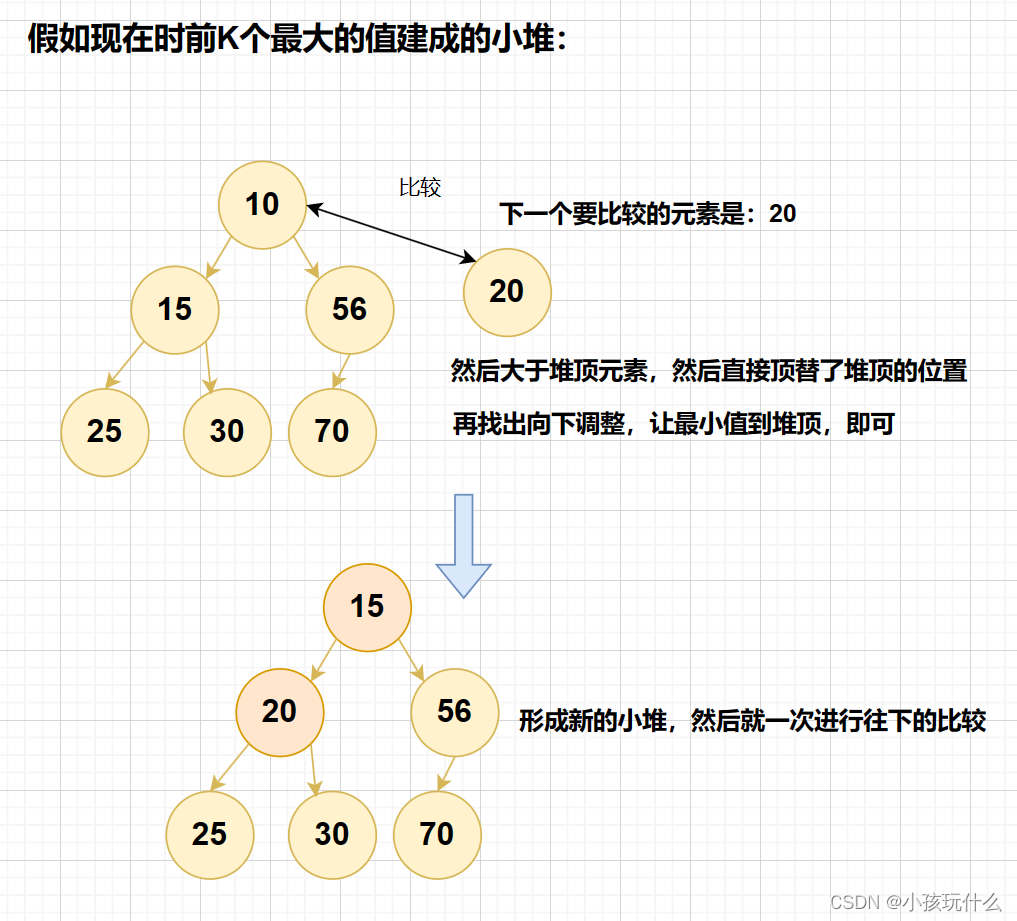
在这里插入图片描述
但是：这样就行了么？在100万个数字里，有什么依据肯定一定输出的就是所有元素中的前K个最大元素呢？
所以我们需要检测的话就需要赋值几个特定的值，假如在设定输出随机值的时候肯定会有其限制：在1~100万的范围里生成随机值，我们赋值几个大于100万的数字就可以判断有没有成功找出最大的K个值；
假如我设定几个值

	a[5] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[531] = 1000000 + 3;
	a[5121] = 1000000 + 4;
	a[115] = 9999999;

代码的实现：

void PrintTopK(int* a, int n, int k)
{
	// 1. 建堆--用a中前k个元素建堆
	int i = 0;
	for (i = (k - 2) / 2; i >= 0; --i)
	{
		Adjustdown(a, n, i);//向下调整算法
	}
	//建升序
	int end = n - 1;
	while (end > 0)
	{
		//最大的数和最后一个数进行交换
		swap(&a[0], &a[end]);
		Adjustdown(a, end, 0);//向下调整算法
		end--;
	}

	// 2. 将剩余n-k个元素依次与堆顶元素交换，不满则则替换
	for (i = n-k-1; i < n; i++)
	{
		if (a[i] > a[0])
		{
			a[0] = a[i];
			Adjustdown(a, k, 0);//向下调整算法
		}
	}
	//打印出来
	for (i = 0; i < k; i++)
	{
		printf("%d\n", a[i]);
	}
}

void TestTopk()
{
	int n = 10000;
	int* a = (int*)malloc(sizeof(int) * n);
	if (a == NULL)
	{
		perror("malloc");
		exit(-1);
	}
	srand(time(0));
	for (int i = 0; i < n; ++i)
	{
		a[i] = rand() % 1000000;
	}
	int k = 5;
	a[5] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[531] = 1000000 + 3;
	a[5121] = 1000000 + 4;
	a[115] = 9999999;
	
	PrintTopK(a, n, k);
}

int main()
{
	TestTopk();
	return 0;
}

最后会打印出来：如果就是你设置的那K个值，那就代表已经实现了TOP-K问题

在这里插入图片描述

链式二叉树

在前面的文章中我们是使用数组的方式实现二叉树，虽然物理存储是和二叉树一样的，但是并不直观的可以感受到；下面我们来使用链表的方式来实现堆，可以更直观的实现二叉树；

二叉树的节点：

二叉树数的每个节点至多有两个度，所以只需要一左一右指针用来链接其子节点就可以完成链式二叉树；

typedef int Treetypedef;

typedef struct TreeNode
{
    Treetypedef val;
    struct TreeNode* left;
    struct TreeNode* right;
}TNode;

初始化节点

初始化节点，设置节点值；

TNode* Node(Treetypedef n)
{
    TNode* ret = (TNode*)malloc(sizeof(TNode));
    if (ret == NULL)
    {
        perror("malloc");
        exit(-1);
    }

    ret->left = NULL;
    ret->right = NULL;
    ret->val = n;
}

实现链式二叉树

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。

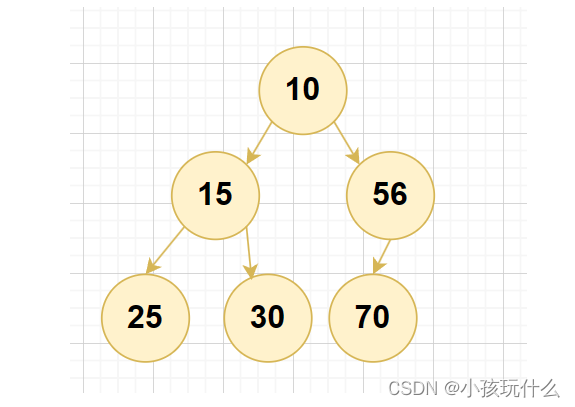
假如要实现下列二叉树：

    struct TreeNode* node1 = Node(10);
    struct TreeNode* node2 = Node(15);
    struct TreeNode* node3 = Node(56);
    struct TreeNode* node4 = Node(25);
    struct TreeNode* node5 = Node(30);
    struct TreeNode* node6 = Node(70);

    node1->left = node2;
    node1->right = node3;
    node2->left = node4;
    node2->right = node5;
    node3->left = node6;

注意：这并不是建造链式二叉树的方式，只是为了今天二叉树的遍历问题，而简易直接搭建的链式二叉树。

二叉树的概念：

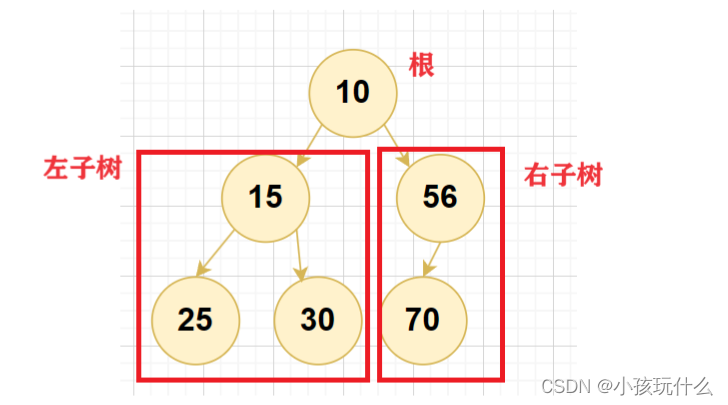
二叉树有两种是：
1.空树。
2.由根节点，根节点的左子树、根节点的右子树组成的。

从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。

二叉树的遍历

二叉树的遍历就是依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。
遍历可分成一下几种：
1. 前序遍历：先访问根节点再访问左子树最后访问右子树；
2. 中序遍历：先访问左子树再访问根节点最后访问右子树；
3. 后序遍历：先访问左子树再访问右子树最后访问根节点；
4. 层序遍历：以层来访问，一层一层往下访问，每一层是从左往右访问；

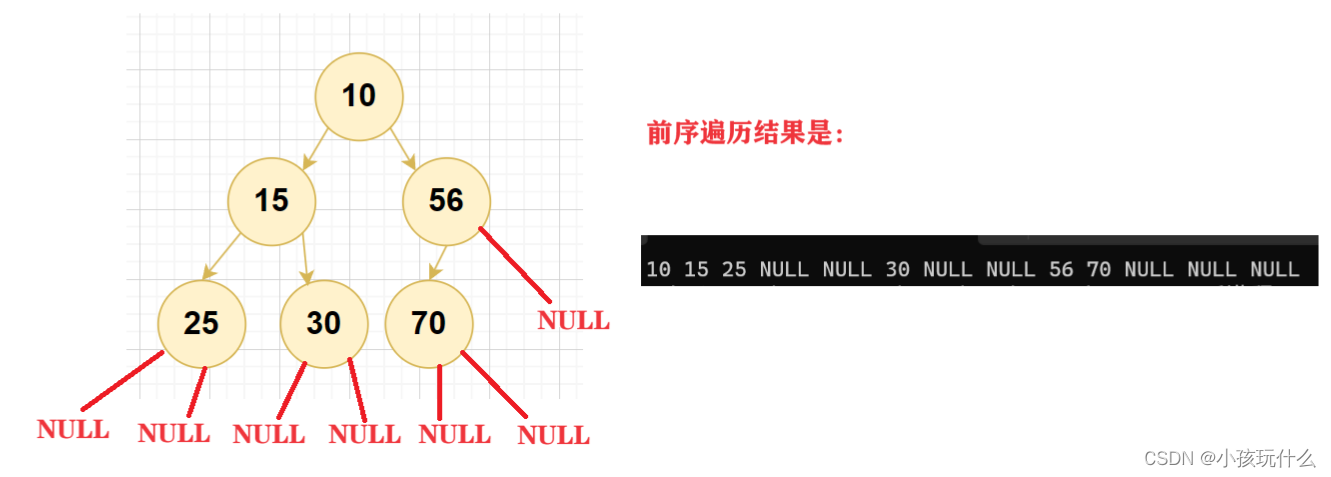
前序遍历

先访问根节点再访问左子树最后访问右子树
访问顺序：根节点—左子树—右子树

// 二叉树前序遍历
void PreOrder(TNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

在这里插入图片描述

中序遍历

先访问左子树再访问根节点最后访问右子树
访问顺序：左子树—根节点—右子树

// 二叉树中序遍历
void InOrder(TNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }

    InOrder(root->left);
    printf("%d ", root->val);
    InOrder(root->right);
}

在这里插入图片描述

后序遍历

先访问左子树再访问右子树最后访问根节点
访问顺序：左子树—右子树—根节点

// 二叉树后序遍历
void PostOrder(TNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }

    PostOrder(root->left);
    PostOrder(root->right);
    printf("%d ", root->val);
}