（闲话）

上了大学后没怎么搞oi，从土木跑路到通信了（提桶开润大成功！），但是一年上两年的课（补的），保研也寄掉了（

说起来自从博客被大学同学发现并在我面前一个一个字读了以后，我：这谁写的，太他ma二次元了，本人决定以后就用比较正常的表述来写这些了（

最近在裸打acm，然后因为只会数据结构派不上用场被队友叫去整点其他部分内容，这两天随便摸了个凸包，整理一下Graham算法，例题还是洛谷的，顺便丢上自己的代码解释步骤：

一、找最低点（y值为min）做起始点root

root必在凸包上就在读入的时候顺便处理掉就行了。为了能顺利找到，root先赋一个大于所有y的值即可。如果出现最低点有很多个，记得一定要找x值最小/最大的点，不然遇到hack数据就没了（原因存疑，个人猜想保留）

for (int a = 1 ; a <= n ; ++ a) {
	scanf("%lf%lf",&s[a].x,&s[a].y);
	if (s[a].y < s[root].y || (s[a].y == s[root].y && s[a].x < s[root].x)) root = a;
} //.x的地方换成大于号也可

此处的s是定义的结构体point，顾名思义。其中的v是存的斜率。这玩意儿干啥用的之后再说

struct point {
	double x,y,v;
};

二、Grahamの排序

排序是精髓。Graham用的排序是以root点为基准，按照其他点和它连线的斜率来决定先扫哪个点再扫哪个点的，这样优势很明显，我意会了一下就记住了，具体原理没找，就不讲了，记得按照斜率扫就行了（

所以，我们要根据这个斜率对原来的一堆点进行排序。我用的是atan2，当然自己算角也行，就是麻烦点。根据下列引用可以得知，atan2如果将点集排序成从右往左扫，它的值是从0升到π，这个值用上文中的结构体point里的v存着。排序的时候cmp按照.v排序就行了。

顺便说一声，直接排的话，遇到斜率相同的点会乱序，遇到hack数据就寄了，所以排序是按照先排斜率再排比较的两点各自与root的距离。

Graham按极角排序但不用距离作为第二关键字会错的原因

/*先按照斜率.v进行比较，再按照距离进行比较*/
bool cmp(point x,point y) {
    return x.v == y.v ? dis(x,s[1]) < dis(y,s[1]) : x.v < y.v;
}

sort(s + 2,s + n + 1,cmp);    //第一个点是root，不用排

那排序就很简单地完成了

三、扫描搜点构成凸包

接下来就是对排序的点遍历，开始包了。我们每次加的点都要满足能构成“当前的凸包”，我是从右往左扫的，所以。。不对，在这之前先介绍二维的叉积吧

就是这么个玩意儿：A.x * B.y - B.x * A.y，AB为俩向量

如果叉出来的结果为正，说明A正旋到B<180°；结果为负，说明A正旋到B>180°。正旋就是从x正向往y正向那方向转

咱以从右往左扫为例，我们要整的凸包此时新的一段一定是要更“往左边拐的”，就是新的凸包边应该是上一个凸包边正旋小于180°能得到的

于是我们把已经构成的凸包的最新的一段，和将要连上的一段整成两个向量（都是从先构造到的点指向后构造的点），叉一下，如果结果为负或0，就说明我们新的边“往右拐”了，这样上一次的凸包的电就不在新的凸包边集上了。而且此时有可能再上一次的边也不满足要求，就还得倒回去接着叉（此时构造向量时，要将之前排除的点的相关部分给换成当前判断的点）。大概是这个样子：

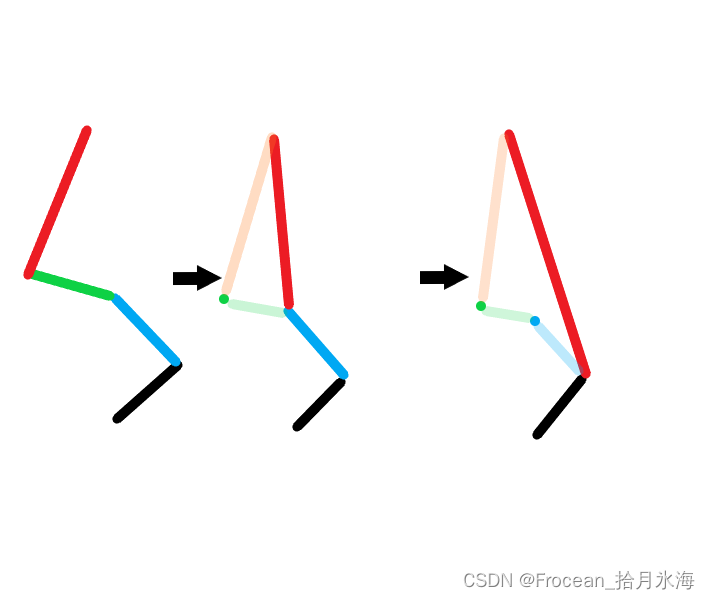
这判断就是jud函数里面的return那部分。为了防止栈被掏空，溯源到root就不继续判断了。

具体代码部分见下：

bool jud(point a,point b,point c,point d) {
	double ix = b.x - a.x,iy = b.y - a.y;
	double jx = d.x - c.x,jy = d.y - c.y;
	return (ix * jy - iy * jx) <= 0;
} //我把向量构成搬到里面来了，小于等于0即判断向量正旋类型

    for (int a = 2 ; a <= n ; ++ a) {
		while (tot > 1 && jud(已处理点构成的向量,新处理点构成的向量) --tot;
		que[++tot] = s[a];
	}

que即为存凸包上的点的栈

四、Blabla

总之这样凸包就已经求出来了，根据题目要求算出要算的东西就行了。 放下上文例题代码：

#include <algorithm>
#include <cstdio>
#include <cmath>
#define N 100010
using namespace std;
struct point {
	double x,y,v;
} s[N],que[N << 1];
double ans = 0;
int n,root = 0,tot = 0;
void swap(point &x,point &y) {point z = x; x = y,y = z;} 
double pf(double x) {return x * x;}	//平方 
double dis(point i,point j) {return sqrt(pf(i.x - j.x) + pf(i.y - j.y));}	//求两点距离 
bool cmp(point x,point y) {return x.v == y.v ? dis(x,s[1]) < dis(y,s[1]) : x.v < y.v;}
bool jud(point a,point b,point c,point d) {
	double ix = b.x - a.x,iy = b.y - a.y;
	double jx = d.x - c.x,jy = d.y - c.y;
	return (ix * jy - iy * jx) <= 0;	//判断正旋角度是否满足题意 
}
int main() {
	s[0].x = 1e6 + 1;
	s[0].y = 1e6 + 1;
	scanf("%d",&n);
	for (int a = 1 ; a <= n ; ++ a) {	//读入点并确定root 
		scanf("%lf%lf",&s[a].x,&s[a].y);
		if (s[a].y < s[root].y || (s[a].y == s[root].y && s[a].x < s[root].x)) root = a;
	}
	swap(s[1],s[root]);
	que[++tot] = s[1];	//root入栈
	 
	for (int a = 2 ; a <= n ; ++ a)	//计算每点与root的斜率 
		s[a].v = atan2(s[a].y - s[1].y,s[a].x - s[1].x);
	sort(s + 2,s + n + 1,cmp);	//按斜率排序 
	
	for (int a = 2 ; a <= n ; ++ a) {	//从右往左扫描 把点丢进凸包 再丢出来一些 
		while (tot > 1 && jud(que[tot - 1],que[tot],que[tot],s[a])) --tot;
		que[++tot] = s[a];
	}
	
	/*根据本题要求求出凸包周长*/
	que[++tot] = s[1];
	for (int a = 1 ; a < tot ; ++ a) ans += dis(que[a],que[a + 1]);
	printf("%.2lf\n",ans);
	return 0;
}