地牢大师问题

文章目录

地牢大师问题
- 前言
- 题目描述
- 题目分析
- - 输入处理
  - 移动方式【和二维的对比】
  - 边界判断问题的解决
- 代码
- 总结

前言

在之前的博客里面，我们介绍了bfs 基础算法的模版和应用,这里我们再挑战一下自己，尝试一个更高水平的题目，加深一下对bfs算法的理解。如果对bfs更多知识感兴趣的话，可以点个关注，后续会继续更新有关知识点的。
往期的文章如下：
红与黑问题（bfs+dfs 解法）

题目描述

你现在被困在一个三维地牢中，需要找到最快脱离的出路！

地牢由若干个单位立方体组成，其中部分不含岩石障碍可以直接通过，部分包含岩石障碍无法通过。

向北，向南，向东，向西，向上或向下移动一个单元距离均需要一分钟。

你不能沿对角线移动，迷宫边界都是坚硬的岩石，你不能走出边界范围。

请问，你有可能逃脱吗？
如果可以，需要多长时间？

输入格式
输入包含多组测试数据。

每组数据第一行包含三个整数 L,R,C
分别表示地牢层数，以及每一层地牢的行数和列数。

接下来是 L 个 R 行 C 列的字符矩阵，用来表示每一层地牢的具体状况。

每个字符用来描述一个地牢单元的具体状况。

其中, 充满岩石障碍的单元格用”#”表示，不含障碍的空单元格用”.”表示，你的起始位置用”S”表示，终点用”E”表示。

每一个字符矩阵后面都会包含一个空行。

当输入一行为”0 0 0”时，表示输入终止。

输出格式
每组数据输出一个结果，每个结果占一行。

如果能够逃脱地牢，则输出”Escaped in x minute(s).”，其中X为逃脱所需最短时间。

如果不能逃脱地牢，则输出”Trapped!”。

数据范围
1≤L,R,C≤100
输入样例：

3 4 5
S....
.###.
.##..
###.#

#####
#####
##.##
##...

#####
#####
#.###
####E

1 3 3
S##
#E#
###

0 0 0

输出样例：

Escaped in 11 minute(s).
Trapped!

题目分析

输入处理

可能有的小伙伴是按照z , x , y 的顺序输入的，其实大可不必，这里的z , x , y
是对称的，也就是说我们对于 z , x , y 三个方向都没有特定的要求，可以随意选取，那么我们只要照常输入就行，相当于交换了坐标系

移动方式【和二维的对比】

看图：在算法坐标系中，二维一般是这样的
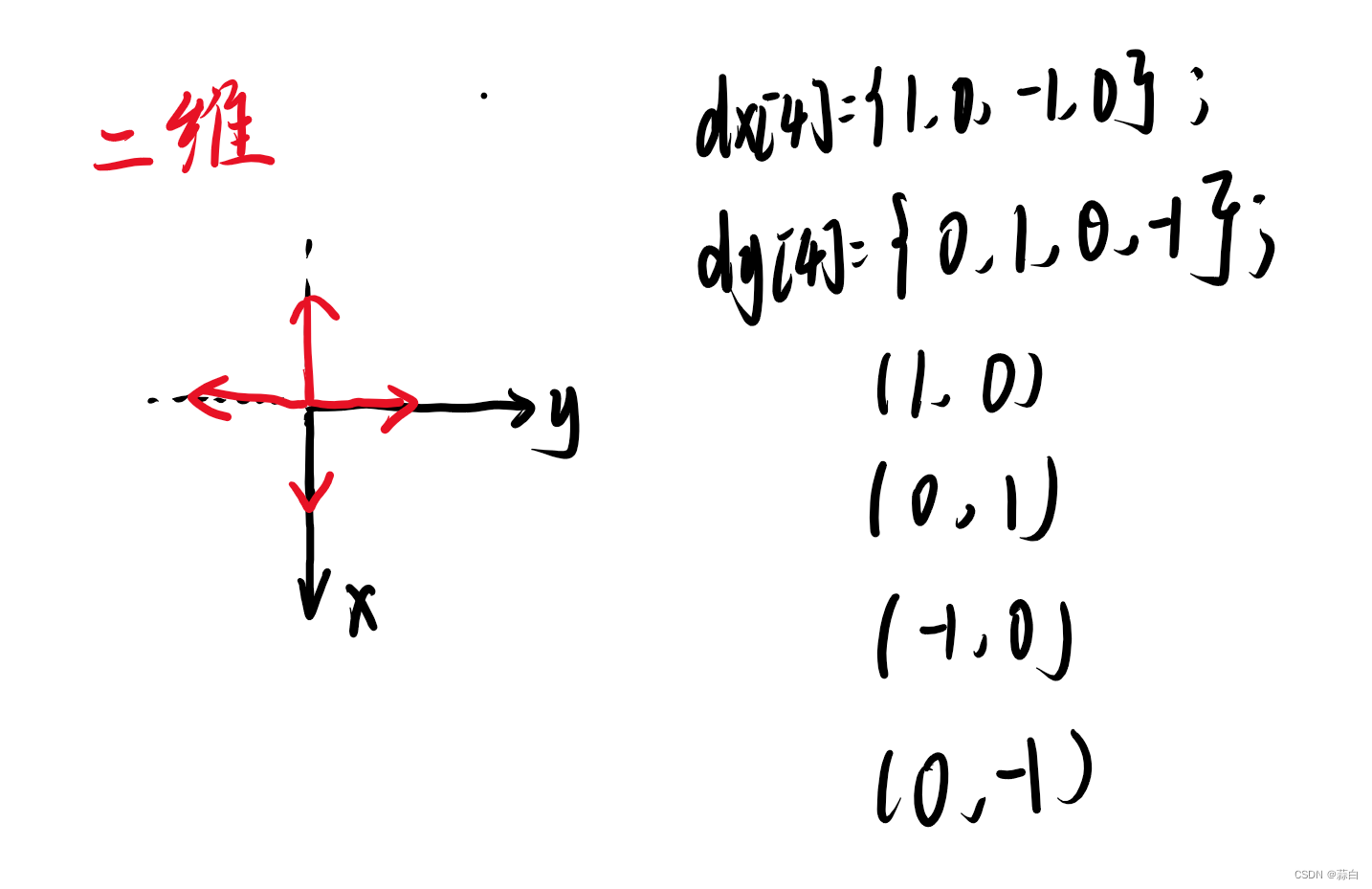
在这里插入图片描述
3维看图：

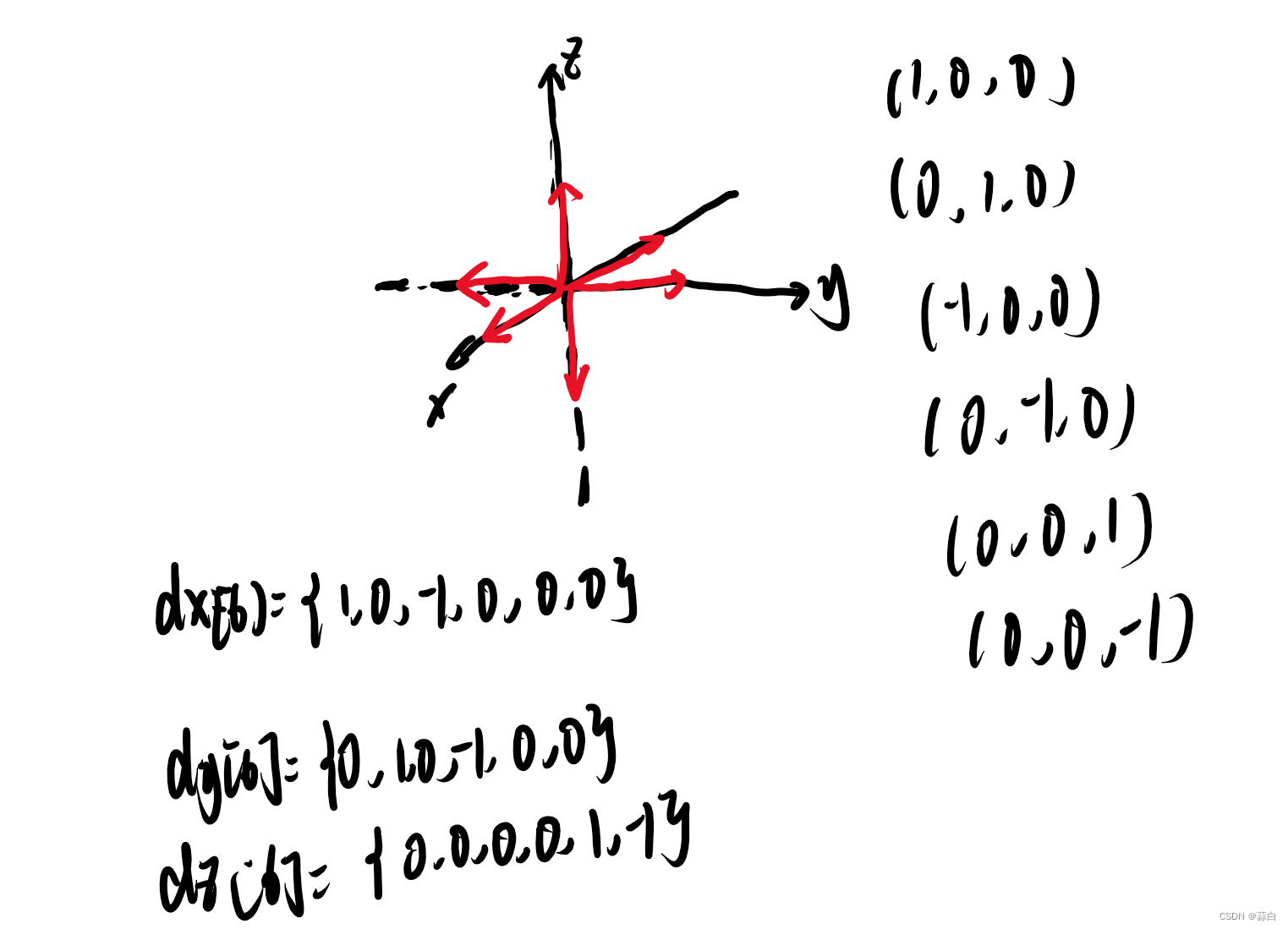
因为每次移动一个长度单位，所以我们在这里是以1为计量单位表示方向。

边界判断问题的解决

接触过bfs算法题目的小伙伴肯定会对边界判断感到不耐烦，这里教大家一个方法摆脱边界判断：
首先将整个地图全部设成#障碍状态，这样后面就不会走到外面去【关键步骤】

memset(g,'#',sizeof g);

其次输入的时候从 1 开始，这里可以避免边界问题，假设我们的输入从 0 开始，那么就会出现 -1 的意外状况

for(int i=1;i<=l;i++){
            for(int j=1;j<=r;j++){
                for(int k=1;k<=c;k++){
                    cin>>g[i][j][k];
                    if(g[i][j][k]=='S'){
                        sx=i,sy=j,sz=k;
                    }
                    if(g[i][j][k]=='E'){
                        ex=i,ey=j,ez=k;
                    }
                }
            }
        }

最后，封死所有走过的路
假设我们不封堵，我们能够走回走过的点，就说明一定有个环，这就无解了，其次，
封过走过的路之后吗，得到的一定就是最小值
一般bfs的处理方法会用一个s t [N]的数组记录是否走过，这里相当于将我们的地图数组一箭双雕。

代码

解释都在代码注释当中啦

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N = 107;

char g[N][N][N];//用于存储地图数据
int d[N][N][N];//用于记录步数
int dx[6]={1,0,-1,0,0,0};
int dy[6]={0,1,0,-1,0,0};
int dz[6]={0,0,0,0,1,-1};
int l,r,c;
struct node{
    int x,y,z;//这里需要对bfs引入 3 哥数据，也就是遍历的队列要包含 3 哥元素
    //所以我们用结构体存储
};
int bfs(int sx,int sy,int sz){
    g[sx][sy][sz]='#';*//将走过的路封死
    d[sx][sy][sz]=0;//将开始的起点举例设为 0 
    queue<node> q;
    q.push({sx,sy,sz});
    while(!q.empty()){
        auto t=q.front();
        q.pop();
        
        for(int i=0;i<6;i++){
            // cout<<dx[i]<<' '<<dy[i]<<' '<<dz[i]<<endl;
            int a=t.x+dx[i];
            int b=t.y+dy[i];
            int c=t.z+dz[i];
            // cout<<a<<b<<c<<endl;
            // cout<<a<<' '<<b<<' '<<c<<endl;
            if(g[a][b][c]!='#'){//直接判断是否为障碍就行
            //不需要俺么劳心费神的操作
                // cout<<g[a][b][c]<<endl;
                if(g[a][b][c]=='.'){
                    q.push({a,b,c});
                    g[a][b][c]='#';
                    d[a][b][c]=d[t.x][t.y][t.z]+1;
                    // cout<<a<<' '<<b<<' '<<c<<endl;
                    // puts("");
                }
                if(g[a][b][c]=='E'){
                    return d[t.x][t.y][t.z]+1;
                }
            }
            
            }
        }
    
    return -1;
}
int main(){
    while(cin>>l>>r>>c,l||r||c){
        memset(g,'#',sizeof g);//由于要输入多个数据
        memset(d,-1,sizeof d);//每次要将数据清零
        int sx,sy,sz;
        int ex,ey,ez;
        for(int i=1;i<=l;i++){
            for(int j=1;j<=r;j++){
                for(int k=1;k<=c;k++){
                    cin>>g[i][j][k];
                    if(g[i][j][k]=='S'){
                        sx=i,sy=j,sz=k;//找到最开始的点
                    }
                    if(g[i][j][k]=='E'){
                        ex=i,ey=j,ez=k;
                        //找到结束的点，后来发现这步操作没有用
                    }
                }
            }
        }
        int t=bfs(sx,sy,sz);
        if(t==-1) printf("Trapped!");
        else printf("Escaped in %d minute(s).",t);
        puts("");
    }
    return 0;
}