模拟大规模电动车充电行为（Matlab实现）

1 模拟大规模充电汽车充电行为

2 Matlab部分代码实现

3 Matlab代码实现

1 模拟大规模充电汽车充电行为

电动汽车EV(Electric Vehicle)具有清洁环保、高效节能的优点,不仅能缓解化石能源危机,而且能够有效地减少温室气体的排放。2015年10月，国务院发布加快EV充电基础设施建设的指导意见,指出到2020年充电基础设施能满足500万辆EV充电需求,预计未来几年我国EV的保有量将大幅增长。然而,规模化EV的无序充电会加大电网负荷的峰谷差,并对电力系统的规划、配电网的电能质量和经济运行以及稳定性带来显著的影响，反之.对EV的充电行为进行有序优化控制,充分发挥EV作为分布式储能元件的优势,能够实现削峰填谷、平抑可再生能源出力波动的功能,并为电网提供调峰、调频等辅助服务。

下图为大规模EV分散接入配电网的场景示意图。EV的管理框架分为配电网代理商、本地代理商和EV 3个层次。配电网代理商分布在高中压HVIMV(High VoltageMedium Voltage)变电层中,负责配电网的安全稳定控制以及EV的有序协调控制;本地代理商分布在中低压MVLV(Mediuim VoltageLow Voltage)变电层中,负责区域EV充电负荷的管控。充电站连接在配电变压器下,配电变压器下除了EV负荷EVL(EV Load)外,还有常规的居民负荷RL(Residential Load)。

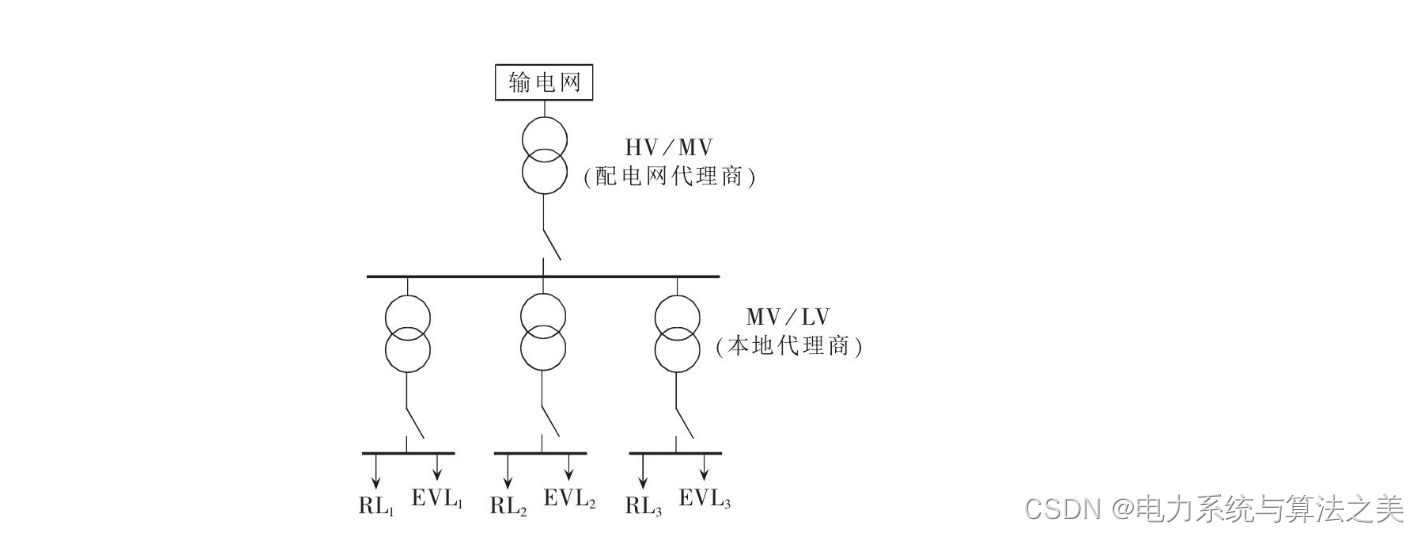
EV进入充电站后,充电智能终端可以获取电池的总容量、荷电状态SoC(State Of Charge)等信息,并通过以太网或专用无线网络提交给本地代理商;用户设置取车时刻以及充电预期荷电状态,充电结束后按实际充电电量向本地代理商支付费用。本地代理商将EV的状态信息和电量需求信息汇集后上传给配电网代理商。配电网代理商采取分时段实时滚动优化的控制策略,当有新的EV接入电网时,更新EV的充电需求信息,执行优化,控制算法,并将充电计划分区下达给各个本地代理商,由本地代理商执行对管控区域内EV的充电控制。

2 Matlab部分代码实现

function [will_charge, best_prior, best_idx] = ...
        CalChargingPrior(is_necessary, cur_soc, arrMCost, ...
                        pindex_start, pindex_end)
    global TOU_EPrice
    global solutions
    global battery_features
    
    % debug by fei
    if (pindex_end - pindex_start + 1) < battery_features.fcharge_periods
        error
    end
    
    % 优先权重系数
    if solutions.start_charging == 4    %如果是组合策略，用上所有系数
        W = solutions.w_coeff;
        % 剩余SOC/最低SOC
        u_s = 1.5 - cur_soc / battery_features.lowest_soc;
    else
        W = zeros(1, 4);
        W(solutions.start_charging) = 1;
        W(4) = 1;
        
    end
    
    % 是否必须充电
        if is_necessary
            u_s = 10000;    %inf
        else
            u_s = 0;
        end
    
    
    nPrior = length(arrMCost);
    % 从某个时刻开始充电的平均电价：元/（瓦＊时段）
    %arrMCost = [];
    % TOC平均电价：元/（瓦＊时段）
    nMTOC = TOU_EPrice.mprice;
    % 充电需用时段
    nTch = single( battery_features.fcharge_periods );
    % 剩余空闲时段
    nTidle = pindex_end - pindex_start + 1;
    arrTidle = single(nTidle) : -1 : nTch;
    % 随机优先 [0 1]
    nRndPr = round(rand);
    arrRndPr = single( nRndPr * rand(1, nPrior) );
    
    % 计算不同时段的充电优先程度
    arrPrior = W(1)*arrRndPr + ...
                W(2)*(1.5 - arrMCost ./ nMTOC) + ...
                W(3)*(1.5 - nTch ./ arrTidle) + ...
                u_s + W(4);
    
    % 最优充电级别与时段
    [p, i] = max(arrPrior);
    best_prior = p;
    best_idx = pindex_start + i - 1;
    % 是否建议充电
    will_charge = (best_prior > 0.5);
end

% 根据不同策略，计算起始充电时段
function [start_cperiod, end_cperiod] = CalChargingPeriods(is_necessary, cur_soc, ...
										pindex_start, pindex_end)
    %global solutions
	global battery_features
	%global mc_params
	%global TOU_EPrice
    
	% 初始参数
    start_cperiod = 0;
	end_cperiod = 0;
    
    earliest = pindex_start;
    latest = pindex_end - battery_features.fcharge_periods + 1;
    
    % 计算从某一时段起充电所需平均电价
    arrMCost = CalChargePrices(earliest:latest);
    
    % 根据策略，计算每一时段充电优先级
    [will_charge, best_prior, best_idx] = ...
        CalChargingPrior(is_necessary, cur_soc, arrMCost, pindex_start, pindex_end);
    
    % 计算策略下的最佳充电起止时间
    if will_charge
        start_cperiod = best_idx;
        end_cperiod = start_cperiod + battery_features.fcharge_periods - 1;
    end
    
end

% m_w_load: 一天中电网各时段负荷平均值，periods_per_day X mean_load
% m_w_charged: 一天中EV各时段充电平均值，periods_per_day X mean_charge
% m_real_trv：一天中EV各时段出行次数平均值，periods_per_day X mean_real_travel
% m_plan_trv：一天中EV各时段计划出行次数平均值，periods_per_day X mean_plan_travel
function [Y, Rmp, Rsc, Rt] = CalIndices(m_w_load, m_w_charged, ...
                                        m_real_trv, m_plan_trv, is_print)
    global TOU_EPrice
    
%     W1 + W2 + W3 = 1.0
%     W1 * 0.275 = W2 * 0.440 = W3 * 0.975 = Si
% 
%     Mi = [0.275 0.440 0.975]
%     Wi = [0.5455    0.3409    0.1538]
%     Si = [0.15 0.15 0.15]
    
    % 指标统计范围 及 权重系数
    RAGmp = [0.05 0.25];	RAGsave=[0.15 0.75];	RAGtrip=[0.95 1.0];
    Wi = [0.4 0.3 0.3];
    
    % 谷峰比 ＝ 充电谷值／充电峰值
%     nWValley = min(m_w_load);
%     nWPeak = max(m_w_load);
%     Rpv = nWValley / nWPeak;

    % 均峰比 ＝ 充电均值／充电峰值
    nWMeanLoad = mean(m_w_load);
    nWPeakLoad = max(m_w_load);
    Rmp = nWMeanLoad / nWPeakLoad;

    % 用户节省电费率 ＝ 1 - 实际电费/最高电费
    nRealCost = sum(m_w_charged .* TOU_EPrice.day_prices);
    nMaxCost = sum(m_w_charged .* max(TOU_EPrice.day_prices));
    Rsc = 1 - nRealCost / nMaxCost;
    
    % 顺利出行率 ＝ 实际里程/计划里程
    nRealTrv = sum(m_real_trv);
    nPlanTrv = sum(m_plan_trv);
    Rt = nRealTrv / nPlanTrv;
    
%     Rmp = 0.218;
%     Rsc = 0.193;
%     Rt = 0.972;
    
    % 综合指标：均峰比，节能率，出行率
    Y = Wi(1) * (Rmp - min(RAGmp)) / (max(RAGmp) - min(RAGmp)) + ...
        Wi(2) * (Rsc - min(RAGsave)) / (max(RAGsave) - min(RAGsave)) + ...
        Wi(3) * (Rt - min(RAGtrip)) / (max(RAGtrip) - min(RAGtrip));
    
    if isnan(Y)
        Y = 0.0;
    end
    
    % 输出结果
    if is_print
        fprintf('----电网负荷：峰值= %d 瓦；均值= %d 瓦；均峰比= %f----\n', nWPeakLoad, nWMeanLoad, Rmp);
        fprintf('----居民用电费用：实际电费= %f 元；最高电费= %d 元；节省率= %f----\n', nRealCost, nMaxCost, Rsc);
        fprintf('----顺利出行情况：实际出行里程= %f 公里；计划出行里程= %d 公里；出行率= %f----\n', nRealTrv, nPlanTrv, Rt);
        fprintf('----综合指标：Y= %f----\n', Y);
    end
end

function [all_indices, mday_indices] = EVPowerLoad(varargin)
    global solutions
    global mc_params
    
    %% 初始化变量
    [nTerms, nEVs] = Initial(varargin);

    %% 模拟 n天 m辆电动汽车
    if ~mc_params.only_show_results
        for t=1:nTerms
%         	for ev_id=1:total_EV
                all_indices = Simulate(t);
%             end
        end
    end
    
    %% 结果统计: 峰谷差，出行受影响概率，充电价格，加入噪声出行等
    result = TempResult('load');
    [grid, ev_behaviour, mday_indices] = StatisticPowerLoad(result);
end


%% initial parameters
function [nTerms, nEVs] = Initial(params)
    
    %% 定义常量
    global mc_params            % MC 参数
    global battery_features     % 电池特性
    global pile_power           % 电桩特性
    global solutions            % 策略
    global behaviours           % 一天用户行为（EVs X Day_Periods）
	%global all_behaviours		% 所有统计时间的用户行为（EVs X All_Periods）
    global t_periods            % 所有统计时段
	global g2v_features			% 充电特性
	global TOU_EPrice			% 分时电价
    global PDF_Travel           % 服从一定概率分布的出行行为
    
    %% 指定参数运行
    if size(params, 2) > 0
        nTerms = params{1};
        nDaysPT = params{2};
        nEVs = params{3};
        chargingStrategy = params{4};
        chargingWCoeff = params{5};
        chargingMinSOC = params{6};
        isOutput = params{7};
        % 用于存储中间结果，而不用保存成文件
        saveResult = false;
        showResultOnly = false;
        
    else  % default values
        %     clear all
        clc
        close all
        
        % 自定义参数值
        nTerms = 4;
        nDaysPT = 25;
        nEVs = 240000;             %EV数量: 2800 5000 62500 240000
        chargingStrategy = 4;
        chargingWCoeff = [0.1512,0.7384,0.1105,0.0196];%ones(1, 4) * 0.25;
        chargingMinSOC = 0.5686;%0.2;
        isOutput = true;
        saveResult = true;         %default:true;
        showResultOnly = true;      %default:false;
        
        seed=15;
        randn('state',seed);
        rand('state',seed);
    end
    
    
    %% 初始化常量
    mc_params.output = isOutput;                            %是否输出结果
    mc_params.cur_day = 1;                                 %当前天数
    %mc_params.cur_ev = 1;                                   %当前汽车ID
    mc_params.periods_per_day = 96;                           %一天划分为若干时段
    mc_params.total_days = nDaysPT;                               %每期模拟天数
    mc_params.all_days = nTerms * mc_params.total_days;       %总共模拟天数
    mc_params.mins_per_period = (24 * 60) / ...
                                mc_params.periods_per_day;	%每个时段的时长
    mc_params.total_periods = mc_params.periods_per_day * ...
                                (mc_params.total_days + 1);       %时段总数
    mc_params.total_EVs = nEVs;
    
    mc_params.cperiod_start_id = 0;
    mc_params.cperiod_end_id = 0;
    mc_params.cperiods = [];
    
    mc_params.eday_soc = ones(nEVs, 1, 'single');          %初始所有EV的SOC为1.0
    
    mc_params.save_result = saveResult;
    mc_params.memory_result = [];                           %用于存储中间结果，而不用保存成文件
	mc_params.only_show_results = showResultOnly;           %只输出统计结果
    
    battery_features.capacity = 100;                        %电池容量
    battery_features.voltage = 230;                         %电池电压
    battery_features.power = battery_features.capacity * ...
                             battery_features.voltage;      %电池总能量
    battery_features.efficiency = 0.3;                      %充电效率
    battery_features.fcharge_duration = 5;                  %充满时间
    battery_features.full_soc = 0.9;                        %soc > 此状态，即认为电池充满
    battery_features.lowest_soc = chargingMinSOC;           %soc < 此状态，必须充电
    battery_features.power_consume_per_km = 0.125e3;        %耗能
	% 满充所需分钟数 及 时段数
    battery_features.fcharge_minutes = battery_features.fcharge_duration * 60;
    battery_features.fcharge_periods = ceil( battery_features.fcharge_minutes / mc_params.mins_per_period );
    
    pile_power = 15e3;                                      %充/放电功率
    solutions.start_charging = chargingStrategy;            %起始充电策略：1.随机充电；2.电价引导充电；3.停车即充电；4.组合策略
    solutions.w_coeff = chargingWCoeff;                     %各种充电影响因素的权重
    solutions.enable_discharge = false;                     %允许V2G的放电模式
    
    
    % 电动汽车类型
    %EV_type = {'bus', 'taxis', 'official_car', 'private_car'};
    
    
    % 1 X (模拟天数 * 每天时段数)
    t_periods = CreatePeriods();
	
	% 计算每时段电网耗用能量 (Wh)
    g2v_features.grid_w_consumed = mc_params.mins_per_period / 60 * pile_power;
    % 计算每时段EV所充能量 (Wh)
    g2v_features.ev_w_charged = g2v_features.grid_w_consumed * battery_features.efficiency;
	
	% 加载分时电价表
	TOU_EPrice = CreateEPriceList();
    
    % 清除结果数据
    if ~mc_params.only_show_results
        ClearResults();
    end
    
    % 加载概率密度函数
    load './data/fitness_travel.mat';
    PDF_Travel = pdf_travel;
end


%% simulate one day
function all_indices = Simulate(t)
    global mc_params
	global behaviours
    %global t_periods
    
    mc_params.cur_day = t;
    %mc_params.cur_ev = ev_id;
    %w_day = mod( (d-1), 7 );
    
	%% clear all behaviours
    ClearAllBehaviours();
	
    %fprintf('－－－－－模拟第 %d 天－－－－－\n', mc_params.cur_day);
    
    %% make the driving & charging plan for all days
    MakeDaysPlan();
    
    %% update all EVs
    UpdateEVs();
    
    %% formating data
    [grid, ev_behaviour, y_indices] = StatDataFormat();
    
	%% combine data of everyday
    all_indices = CombineData(grid, ev_behaviour, y_indices);
    
    %% update params
    UpdateMCParams();
end

function all_periods = CreatePeriods()
    global mc_params
    
    % construct the period array
    all_periods = int32( 0 : (mc_params.total_periods - 1) ) * ...
                    mc_params.mins_per_period;
end


function ClearAllBehaviours()
    global behaviours
    
    % init array for EV behaviours
    behaviours = [];
    behaviours.v_is_driving = logical([]);
    behaviours.v_plan_driving = logical([]);
    behaviours.v_driving_km_pp = single([]);
    behaviours.v_driving_cost_power = single([]);
    behaviours.v_able_charge = logical([]);
    behaviours.v_is_charging = logical([]);
	behaviours.v_ev_w_charged = single([]);
    behaviours.v_ev_w_discharged = single([]);
    behaviours.grid_power_load = single([]);
    behaviours.soc = single([]);
end

function ClearResults()
    global mc_params
    global solutions
    
    ndays = mc_params.all_days;
    
    % init & save temporary data
    result.grid.power_load = zeros(ndays, mc_params.periods_per_day, 'single');
    result.grid.power_charged = zeros(ndays, mc_params.periods_per_day, 'single');
    result.grid.power_V2G = zeros(ndays, mc_params.periods_per_day, 'single');
    
    result.ev_behaviour.trv_num_per_period = zeros(ndays, mc_params.periods_per_day, 'int32');
    result.ev_behaviour.plan_trv_num_per_period = zeros(ndays, mc_params.periods_per_day, 'int32');
    result.ev_behaviour.cha_num_per_period = zeros(ndays, mc_params.periods_per_day, 'int32');
    result.ev_behaviour.dischar_num_per_period = zeros(ndays, mc_params.periods_per_day, 'int32');
    
    result.y_indices = zeros(ndays, 1, 'single');
    
    TempResult('save', result);
    
    clear 'result';
end


function all_indices = CombineData(grid, ev_behaviour, y_indices)
	global behaviours
    %global all_behaviours
    global solutions
    global mc_params
	
    ndays = mc_params.all_days;
    cur_day = ((mc_params.cur_day - 1) * mc_params.total_days + 1) : ...
        mc_params.cur_day * mc_params.total_days;
    
	% 加载临时数据
    result = TempResult('load');
    
    % 合并每天的电网负荷及EV行为
    result.grid.power_load(cur_day, :) = grid.power_load;
    result.grid.power_charged(cur_day, :) = grid.power_charged;
    result.grid.power_V2G(cur_day, :) = grid.power_V2G;
    
    result.ev_behaviour.trv_num_per_period(cur_day, :) = ev_behaviour.trv_num_per_period;
    result.ev_behaviour.plan_trv_num_per_period(cur_day, :) = ev_behaviour.plan_trv_num_per_period;
    result.ev_behaviour.cha_num_per_period(cur_day, :) = ev_behaviour.cha_num_per_period;
    result.ev_behaviour.dischar_num_per_period(cur_day, :) = ev_behaviour.dischar_num_per_period;
    
    result.y_indices(cur_day, :) = y_indices;
    
    % save temporary data
    TempResult('save', result);
    
    % clear data from memory
    all_indices = result.y_indices;
    clear 'result';
end


function UpdateMCParams()
    global mc_params
    global behaviours
    
    % clear mc prams
    mc_params.total_periods = mc_params.periods_per_day * ...
                                (mc_params.total_days + 1);       %时段总数
    
    mc_params.cperiod_start_id = 0;
    mc_params.cperiod_end_id = 0;
    mc_params.cperiods = [];
    
    % record soc for all EVs when one day is ending
    mc_params.eday_soc = behaviours.soc(:, end);
end

function [is_necessary, soc_start] = IsNecessaryCharge(ev_id, pindex_start, pindex_end)
	%global behaviours
    global battery_features
    
    % soc低于0.2时必须充电
	soc_start = GetPreviousSOC(ev_id, pindex_start);
	is_necessary = (soc_start < battery_features.lowest_soc);
end